排序之拓“谱”排序

1.基本概念

拓扑排序是对一个有向无环图(Directed Acyclic Graph, 简称DAG)进行的一种排序，它将图中的所有顶点排成一个线性序列，使得对于图中任意一对顶点u和v，若存在一条从u到v的边，则u在线性序列中出现在v之前。这样的线性序列被称为满足拓扑次序的序列，简称拓扑序列。简单来说，拓扑排序是由某个集合上的一个偏序得到该集合上的一个全序的操作。

拓扑排序的应用学科主要是计算机科学中的图论。它通常用于描述一项工程或系统的进行过程，如计划、施工、生产、程序流程等，其中每个工程都可以分解为若干个子工程（称为活动）。要完成整个工程，需要完成所有活动，而这些活动的执行通常有某些先决条件，即一些活动必须先于另一些活动完成。拓扑排序可以用来确定这些活动的执行顺序，或者测试一个有向图是否存在环。

拓扑排序是针对有向无环图（DAG）的一种排序方法，常见的应用案例有：

1. 任务调度：在一个项目中，任务之间可能存在依赖关系，需要按照依赖关系进行排序，确定任务的执行顺序。

2. 编译顺序：在编译过程中，源文件之间可能存在依赖关系，需要按照依赖关系进行排序，确定编译的顺序。

3. 课程安排：在大学或学校的课程表中，不同课程之间可能存在先后顺序的依赖关系，需要按照依赖关系进行排序，确定学生的上课顺序。

4. 项目依赖关系解析：在软件开发中，不同的软件模块之间可能存在依赖关系，需要按照依赖关系进行排序，确定模块的加载顺序。

5. 网络拓扑排序：在计算机网络中，不同的网络节点之间可能存在依赖关系，需要按照依赖关系进行排序，确定网络节点的通信顺序。

总之，拓扑排序在涉及到依赖关系的场景中都有应用，用于确定事物的顺序或规划任务的执行顺序。

2.整体思想

具体来说，拓扑排序的过程包括：

• 对于一个有向无环图G，将其所有顶点排成一个线性序列。
• 在这个序列中，如果存在一条从顶点u到顶点v的边，那么顶点u必须出现在顶点v之前。
• 拓扑排序可以用来判断一个有向图是否存在环：如果网中所有顶点都在它的拓扑排序序列中，那么该有向图必定不存在环；反之，如果对一个有向图不能进行拓扑排序，则必定存在环。

拓扑排序的实现可以通过不同的算法，如深度优先搜索（DFS）或广度优先搜索（BFS）等，具体实现方式取决于具体的应用场景和需求。

这样说太抽象了，像我恩师说得：“如果理解一篇东西像看论文一样的话，可能人点进去就关了。”

总结前我们先要知道“度”是什么？将两个节点连接在一起的就叫度，在有向图中，度分为入度，出度，入度就是由上一个节点的度来连接这个节点的就叫入度，出度就是由这个节点去连接下一个节点就叫出度，在无向图中只有一个度。（！！！注意一个重点：在有向图中，入度为零的节点就是起点，出度为零的点就是终点。）

简单理解一下拓扑排序基本就是将入度为零的节点输出，在更新一下，将输出的节点有关的都全部都删除，看哪个节点变成了零在输出它，直到每个节点都输出了以后，整个排序就结束了。

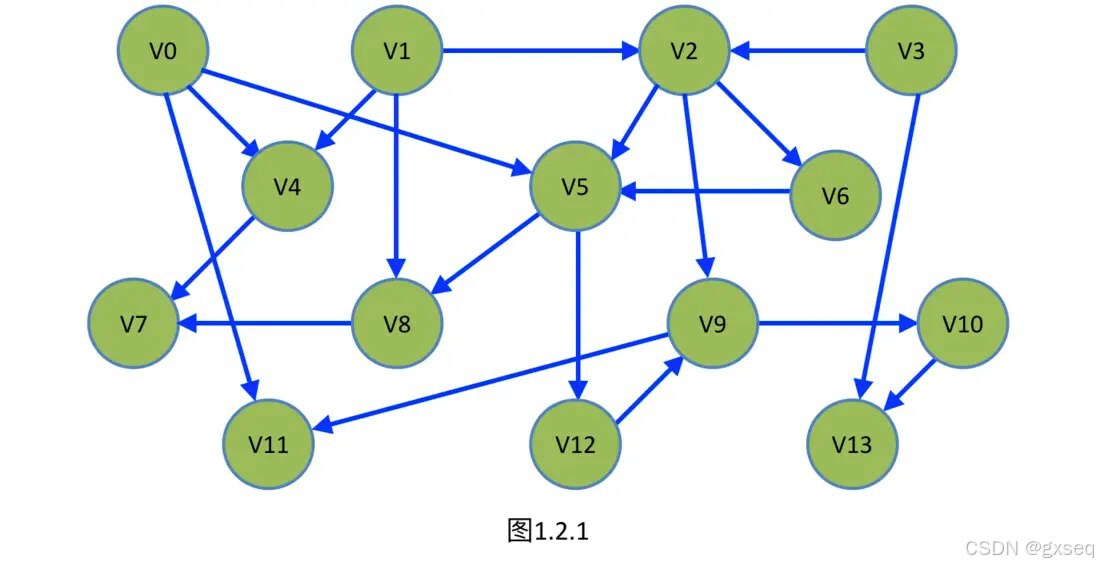
就如同这个图一样

拓扑排序就好比如，从原厂生产了一件东西，它给了物流中心，然后物流中心再给到各个地方的快递站，快递站再将每个东西送到驿站中，最后由人过来取。这样一个流程。

将完了原理和如何实现，那怎样把它转换到代码上呢？

3.代码展现

这里我依旧拿一道模板题来讲解

B3644 【模板】拓扑排序 / 家谱树

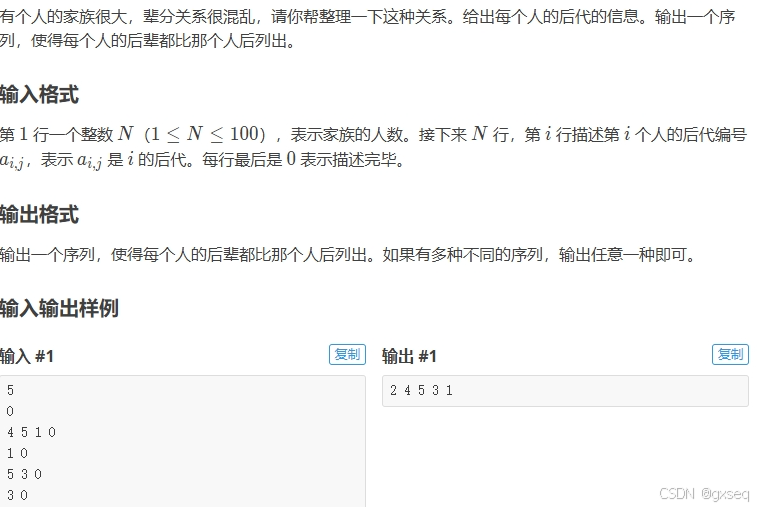
题中想让我们将给出的家族排一个序，使长辈比晚辈先输出，以为题目中给的是家谱，所以这道题的图肯定是个有向图并且没有环（毕竟你的长辈还能当你的晚辈吗？这肯定不现实）那我们首先就要想到拓扑排序。

（金局：无向想并查，又向想拓扑）

（要了解拓扑的请看我上篇博客并查“鸡”保姆级讲解）

依照拓扑排序的思路我们就能做出来这题，思路都先想好了，那就上代码：

#include<bits/stdc++.h>
using namespace std;
int n, x;
vector<int>vec[107];//这里我们使用邻接表来帮助我们排序 
int cnt[107];
queue<int>q;//定义一个队列方便我们更好地排序 
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		while (true) {
			cin >> x;
			if (x == 0) {
				break;
			}
			vec[i].push_back(x);//每输入一个i的子节点，就把它储存起来 
			cnt[x]++;//每储存一个x就让cnt[x]++，表示x总共有多少个入度
		}
	}
	for (int i = 1; i <= n; i++) {
		if (cnt[i] == 0) {// 如果一开始i的入度就为零说明i为起点 
			q.push(i);//就将i推进队列中 
		}
	}
	while (!q.empty()) {//如果队列不为空就说明还有节点没有排序完 
		cout << q.front()<<' ';//输出队首 
		for (int i = 0; i < vec[q.front()].size(); i++) {
			cnt[vec[q.front()][i]]--;//因为队首输出了，所以有关队首的所有节点都要把入度减一 
			if (cnt[vec[q.front()][i]] == 0) {//如果入度为零了，说明没有结点指向它了，就把它推入队列中 
				q.push(vec[q.front()][i]);
			}
		}
		q.pop();//弹出队首 
	}
	return 0;
}

4.做题巩固

P2712 摄像头

题中这些松鼠想去抢劫食品店，让我们帮助它们（内心:这些松鼠太胆大妄为了）

松鼠们把这些摄像头都给同一编号，摄像头能砸毁的条件就是该摄像头的位置不能被其它摄像头拍到，这不就跟拓扑排序一样吗？能弹出一个节点的条件就是它的入度为零，其它节点没有跟它相连的。

那这题我么就直接拓扑排序做就行了。

#include <bits/stdc++.h>
using namespace std;
const int N = 710;
int h[N], e[N], ne[N], idx, d[N],state[N];
int q[N], hh = 0, tt = -1;
int n;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void topsort() {
    for (int i = 1;i<N;i++) {
        if (state[i]&&d[i] == 0) q[++tt] = i;
    }
    while (hh <= tt) {
        int a = q[hh++];
        for (int i = h[a];i != 0;i = ne[i]) {
            int b = e[i];
            d[b]--;
            if (d[b] == 0&&state[b]==1) q[++tt] = b;
        }
    }
    if (tt == n - 1) cout << "YES ";
    else cout << n-1-tt;
}
int main() {
    
    cin >> n;
    for (int i = 1;i <= n;i++) {
        int x, m;
        cin >> x >> m;
        state[x] = 1;
        while (m--) {
            int a;
            cin >> a;
            add(x, a);
            d[a]++;
        }
    }
    topsort();

}

5.变式分析

1352：【例4-13】奖金

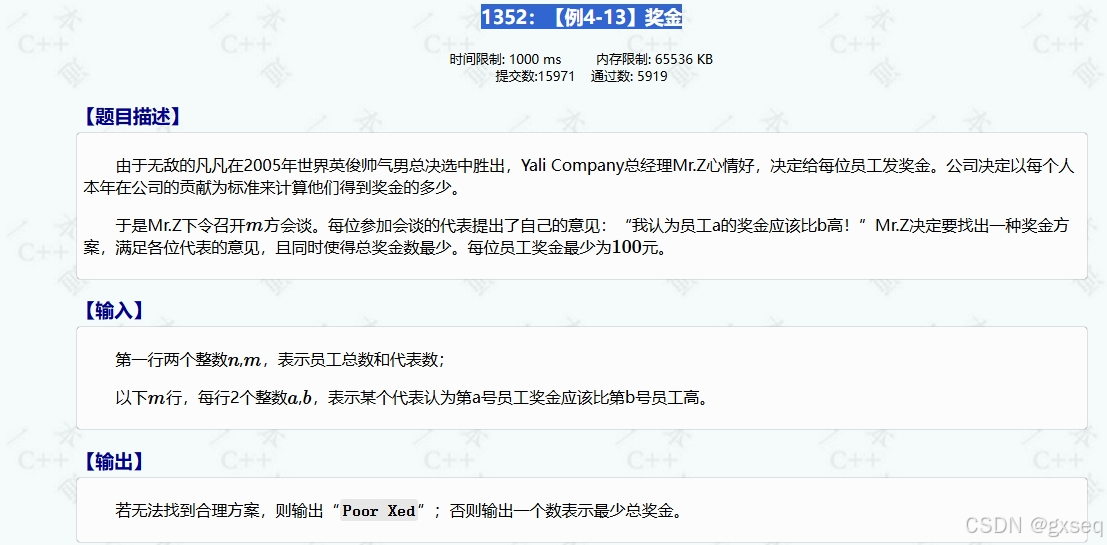
这题说给出员工总数和代表数，每个代表都会提一个要求让谁比谁的奖金多，要找一种奖金方案，使得满足各位代表的意见。

这题乍一看好像可以用并查集做，but它这题规定了who比who的奖金多，所以这题的图是个有向图，那我们只好用拓扑排序了，但这题它说a比b工资高，如果像之前一样让a当父节点那这题就不好做了，所以这题我们反向连边。将所有节点都遍历一遍每个节点都比都比它的父节点工资高，如果有节点没遍历上，工资没变的话，它就形成了一个环就无法找到合理方案。

具体看代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
const int N=2e4+9;
int  n , m ; 
int a , b; 
vector<int>g[N];
queue<int>q;
int p[N];
int in[N];
int flag;
int vis[N];
int v[N];//存储最长路
long long ans; 
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>a>>b;
		g[b].push_back(a);//反向建边 
		in[a]++;
	}
	
	if(m == 0){
		int tmp = n*100;
		cout<<tmp;
		return 0;
	}
	for(int i = 1;i<=n;i++){
		if(!in[i]) q.push(i);
		v[i] = 100;
	}
	int j = 1;
	while(!q.empty()){	
		int x = q.front();q.pop();
		for(int i = 0;i<g[x].size();i++){
			vis[g[x][i]] = 1;
			if(v[g[x][i]]<v[x]+1) v[g[x][i]] = v[x] + 1;
			in[g[x][i]]--;
			if(in[g[x][i]] <= 0) q.push(g[x][i]);
		}
	}
	
	for(int i = 1;i <= n ;i++){
		
		ans+=v[i];
	}
	
	if(ans == n*100){
		cout<<"Poor Xed";
		return 0;
	}else{
		cout<<ans;
	}
 

	return 0;
}

对拓扑排序的内容作者就讲完了。感谢各位的观看。

最后给作者点一个赞和关注吧。

求个赞，阿里嘎多。