排序可以说是套路最多的基本算法了,今天来了兴致,那就总结一下这十大排序算法吧。
冒泡法:
这可以算是知名度最高的算法之一了吧,可以说不会这个算法都不好意思说自己写过代码。冒泡排序是最简单的排序之一了,其大体思想就是通过与相邻元素的比较和交换来把小的数交换到最前面。这个过程类似于水泡向上升一样,因此而得名。不多说了,直接上代码:
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
int main()
{
for(int i=0;i<LEN-1;i++)
{
for(int j=i+1;j<LEN;j++)
{
if(a[i]>a[j])
swap(a[i],a[j]);
}
}
for(int i=0;i<LEN;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
选择排序:
冒泡排序的孪生兄弟吧,它和冒泡不一样的地方是,它没冒泡那么“愣头青”,而是更成熟的“谋定而后动”,找到了目标再进行交换。
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
int main()
{
int k;
for(int i=0;i<LEN-1;i++)
{
k=i;
for(int j=i+1;j<LEN;j++)
{
if(a[k]>a[j])
k=j;
}
if(k!=i)
swap(a[k],a[i]);
}
for(int i=0;i<LEN;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
插入排序:
打过扑克的人应该都熟悉这个算法,抽到一张牌,将它插到合适位置,这就是这个算法的思想。
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
int main()
{
int index,temp;
for(int i=1;i<LEN;i++)
{
//一步步慢慢向前进
index=i; temp=a[i];
while(index>0 && temp<a[index-1])
{
swap(a[index],a[index-1]); --index;
}
}
for(int i=0;i<LEN;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
快速排序:
快速排序一听名字就觉得很高端,在实际应用当中快速排序确实也是表现最好的排序算法。快速排序虽然高端,但其
实其思想是来自冒泡排序,冒泡排序是通过相邻元素的比较和交换把最小的冒泡到最顶端,而快速排序是比较和交换
小数和大数,这样一来不仅把小数冒泡到上面同时也把大数沉到下面。
举个栗子:对5,3,8,6,4这个无序序列进行快速排序,思路是右指针找比基准数小的,左指针找比基准数大的,交换之。
5,3,8,6,4 用5作为比较的基准,最终会把5小的移动到5的左边,比5大的移动到5的右边。
5,3,8,6,4 首先设置i,j两个指针分别指向两端,j指针先扫描(思考一下为什么?)4比5小停止。然后i扫描,8比5大停止
。交换i,j位置。
5,3,4,6,8 然后j指针再扫描,这时j扫描4时两指针相遇。停止。然后交换4和基准数。
4,3,5,6,8 一次划分后达到了左边比5小,右边比5大的目的。之后对左右子序列递归排序,最终得到有序序列。
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
void quickSort(int l,int r)
{
if(l>=r)
return;
int i=l,j=r,x=a[l];//以第一个数为基准
while(i<j)
{
while(i<j && a[j]>=x)//从右向左找第一个小于x的数
j--;
if(i<j)
a[i++]=a[j];
while(i<j && a[i]<=x)//从左向右找第一个大于x的数
i++;
if(i<j)
a[j--]=a[i];
}
a[i]=x;
quickSort(l,i-1);
quickSort(i+1,r);
}
int main()
{
quickSort(0,LEN-1);
for(int i=0;i<LEN;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
堆排序:
通过建立大根堆或者小根堆进行排序。想升序排序就使用大顶堆,反之使用小顶堆。(因为每次都将堆顶元素放到
末尾)
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
//以大根堆为例
void buildHeap(int id, int maxid)
{
int left=id<<1|1;
int right=left+1;
if(left<=maxid)
{
buildHeap(left, maxid);
if(a[id]<a[left])
swap(a[id],a[left]);
}
if(right<=maxid)
{
buildHeap(right, maxid);
if(a[id]<a[right])
swap(a[id],a[right]);
}
}
void heapSort()
{
int len=LEN-1;
while(len)
{
buildHeap(0,len);
swap(a[0],a[len]);
--len;
}
}
int main()
{
heapSort();
for(int i=0;i<LEN;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
希尔排序:
希尔排序是插入排序的一种高效率的实现,也叫缩小增量排序。简单的插入排序中,如果待排序列是正序时,时间
复杂度是O(n),如果序列是基本有序的,使用直接插入排序效率就非常高。希尔排序就利用了这个特点。基本思想
是:先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时再对全体
记录进行一次直接插入排序。
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
void insertSort(int l,int r)
{
int index,temp;
for(int i=l+1;i<=r;i++)
{
//一步步慢慢向前进
index=i; temp=a[i];
while(index>l && temp<a[index-1])
{
swap(a[index],a[index-1]); --index;
}
}
}
//分三级增量 分别为3 2 1
int gap=3;
void shell_sort()
{
for(int i=gap;i>=1;i--)
{
for(int j=0;j+i<LEN;j++)
{
insertSort(j,j+i);
}
}
}
int main()
{
shell_sort();
for(int i=0;i<LEN;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
归并排序:
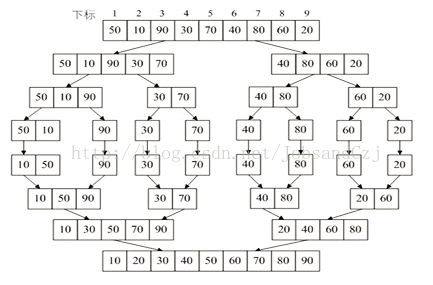
归并排序是另一种不同的排序方法,因为归并排序使用了递归分治的思想,所以理解起来比较容易。其基本思想
是,先递归划分子问题,然后合并结果。把待排序列看成由两个有序的子序列,然后合并两个子序列,然后把子
序列看成由两个有序序列。。。。。倒着来看,其实就是先两两合并,然后四四合并。。。最终形成有序序列。
空间复杂度为O(n),时间复杂度为O(nlogn)。
还是上张图吧:
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
void merge(int l1,int r1,int l2,int r2)
{
int cou=0;
int temp[LEN]; //临时数组
int i,j;
for(i=l1,j=l2;i<=r1&&j<=r2;)
{
if(a[i]<a[j])
temp[cou++]=a[i++];
else
temp[cou++]=a[j++];
}
while(i<=r1)
temp[cou++]=a[i++];
while(j<=r2)
temp[cou++]=a[j++];
cou=0;
for(int i=l1;i<=r2;i++)
{
a[i]=temp[cou++];
}
}
void mergeSort(int l,int r)
{
if(l==r)
return;
int mid=(l+r)/2;
mergeSort(l,mid);
mergeSort(mid+1,r);
merge(l,mid,mid+1,r);
}
int main()
{
mergeSort(0,LEN-1);
for(int i=0;i<LEN;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}
计数排序:
如果在面试中有面试官要求你写一个O(n)时间复杂度的排序算法,你千万不要立刻说:这不可能!虽然前面基于比
较的排序的下限是O(nlogn)。但是确实也有线性时间复杂度的排序。,只不过有前提条件,就是待排序的数要满足
一定的范围的整数,而且计数排序需要比较多的辅助空间。其基本思想是,用待排序的数作为计数数组的下标,统
计每个数字的个数。然后依次输出即可得到有序序列。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define LEN 6
#define MAX 20
int a[]={10,9,11,6,20,17};
int counter[MAX+1]; //计数数组
int main()
{
memset(counter,0,sizeof(counter));//数组清零
for(int i=0;i<LEN;i++)
{
counter[a[i]]++;
}
for(int i=0;i<=MAX;i++)
{
for(int j=0;j<counter[i];j++)
cout<<i<<" ";
}
cout<<endl;
return 0;
}
桶排序:
假设有一组长度为N的待排关键字序列K[1....n]。首先将这个序列划分成M个的子区间(桶) 。然后基于某种映射函
数 ,将待排序列的关键字k映射到第i个桶中(即桶数组B的下标i) ,那么该关键字k就作为B[i]中的元素(每个桶B[i]
都是一组大小为N/M的序列)。接着对每个桶B[i]中的所有元素进行比较排序(可以使用快排)。然后依次枚举输出
B[0]....B[M]中的全部内容即是一个有序序列。bindex=f(key) 其中,bindex 为桶数组B的下标(即第bindex个桶),
k为待排序列的关键字。桶排序之所以能够高效,其关键在于这个映射函数,它必须做到:如果关键字k1<k2,那
么f(k1)<=f(k2)。也就是说B(i)中的最小数据都要大于B(i-1)中最大数据。很显然,映射函数的确定与数据本身的特
点有很大的关系。
#include<iostream>
#include<algorithm>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
int bucket[3][LEN];
int main()
{
int temp;
memset(bucket,0,sizeof(bucket));
for(int i=0;i<LEN;i++)
{
temp=a[i]/10;
int index=++bucket[temp][0];
bucket[temp][index]=a[i];
}
for(int i=0;i<3;i++)
{
if(bucket[i][0])
sort(bucket[i]+1, bucket[i]+1+bucket[i][0]);//这里耍个赖皮 桶里的排序方法可自行选择
}
for(int i=0;i<3;i++)
{
for(int j=1;j<=bucket[i][0];j++)
{
cout<<bucket[i][j]<<" ";
}
}
cout<<endl;
return 0;
}
基数排序:
基数排序又是一种和前面排序方式不同的排序方式,基数排序不需要进行记录关键字之间的比较。基数排序是一种借
助多关键字排序思想对单逻辑关键字进行排序的方法。所谓的多关键字排序就是有多个优先级不同的关键字。比如说
成绩的排序,如果两个人总分相同,则语文高的排在前面,语文成绩也相同则数学高的排在前面。。。如果对数字进
行排序,那么个位、十位、百位就是不同优先级的关键字,如果要进行升序排序,那么个位、十位、百位优先级一次
增加。基数排序是通过多次的收分配和收集来实现的,关键字优先级低的先进行分配和收集。
我选择了队列这个数据结构,因为我觉得队列比较合适,但实现起来并不让我满意,如果大牛们有指教,非常欢迎!
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
#define LEN 6
int a[]={10,9,11,6,20,17};
queue<int> que[10];
int counter[10];
//获取这个整数有几位
int getNumberOfInt(int a)
{
int cou=0;
while(a)
{
++cou; a/=10;
}
return cou;
}
//获取整数a的第n位数
int getNum(int a,int n)
{
for(int i=0;i<n-1&&a;i++)
{
a/=10;
}
return a%10;
}
int main()
{
int maxN=0;
int temp;
memset(counter,0,sizeof(counter));
//计算得出最多循环几轮
for(int i=0;i<LEN;i++)
maxN=max(maxN,getNumberOfInt(a[i]));
//第一轮先入队列
for(int i=0;i<LEN;i++)
{
temp=a[i]%10;
que[temp].push(a[i]);
}
for(int k=2;k<=maxN;k++)
{
for(int ii=0;ii<10;ii++)
counter[ii]=que[ii].size();//统计该队列原本个数
for(int i=0;i<10;i++)
{
for(int j=0;j<counter[i];j++)
{
int t=que[i].front();
int index=getNum(t,k);
que[index].push(t);
que[i].pop();
}
}
}
for(int i=0;i<10;i++)
{
while(!que[i].empty())
{
cout<<que[i].front()<<" "; que[i].pop();
}
}
cout<<endl;
return 0;
}
























 427
427

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








