【魏先生搞定深度学习数学系列】克莱姆法则及其推论

       克莱姆法则（由线性方程组的系数确定方程组解的表达式）是线性代数中一个关于求解线性方程组的定理，它适用于变量和方程数目相等的线性方程组。如果将行列式系数理解为矩阵，那么仅对方阵有效。

一、相关概念储备

1.齐次和非其次线性方程组  

        首先是线性方程组的概念，线性方程组的本质是一组向量对另一个向量的线性表示。如果把这一组向量视为一个基，那么求解一个线性方程组，就是找出被表示向量在一组基上的坐标。即形如Ax=b的表示，就是线性方程组。

        继而是齐次的概念，齐次线性方程组的常数项全部为零，非齐次方程组的常数项不全为零。形如Ax=0，就是齐次的；而Ax=b 且b≠0，就是非齐次的。

        如果用多项式来理解，则可以看下面的行列式：

        

       其中A为系数矩阵，X为未知数组成的向量，β为常数向量。如果β为0，则是其次线性的，如果β不为0，则为非其次线性的。

二、克莱姆法则定义及其推论

1.法则内容

     n元非齐次线性方程组中：

      系数构成的行列式称为该方程组的系数行列式D，即：

                   

       若线性方程组的系数矩阵可逆（非奇异），即系数行列式 D≠0，则线性方程组有唯一解，其解为：

     Dj是把D中第j列元素对应地换成常数项而其余各列保持不变所得到的行列式。如：

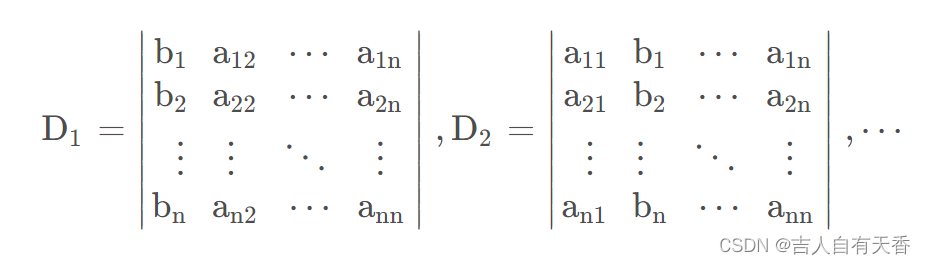
2.法则使用前提

   （1）系数行列式D不能等于0：如果=0，即方阵不满秩，则有多个解；则行列式系数参数矩阵可以理解为不是方阵，有多个解。

   （2）线性方程组： X的最高次幂为1，即多元一次       

3.法则产生的推论

        推论1：n元齐次线性方程组有唯一零解的充要条件是系数行列式不等于零，系数矩阵可逆。（矩阵可逆=矩阵非奇异=矩阵对应的行列式不为0=满秩=行列向量线性无关）。

        如果系数行列式不等于0，则 系数矩阵可逆，又因为是其次方程，所以常数向量β为0，那么D1...Dn行列式均为0，因此方程有唯一0解。

        推论2：n元齐次线性方程组有非零解的充要条件是系数行列式等于零。

        实际推论2可以从上面推论1得来。

参考文章：

克莱姆法则（Cramer's Rule）_jackghq的博客-CSDN博客

Cramer`s Rule 克莱姆法则（克拉默法则）_sam_kql的博客-CSDN博客 （重点推荐）