卡特兰数总结

卡特兰数的三种基本表示方式：

$f(n)=\frac{C_{2n}^n}{n+1}=\sum _{i=1}^{n}f(i-1)\ast f(n-i)=C_{2n}^n-C_{2n}^{n-1}$

卡特兰数经典模型：

有$n$个$0$和$n$个$1$，有多少种排列方式使得任意一个前缀中，$1$的个数不少于$0$的个数？

卡特兰数经典模型的证明：

我们可以在数轴上看这个问题，从原点出发，将$1$看成向右上走一步，$0$看成向右下走一步，那么走完这$2n$步会到达点$(2n,0)$。不做限制时的走法是$C_{2n}^n$，即在$2n$步中选$n$步放$1$。当我们加上限制，任意一个前缀中，$1$的个数不少于$0$的个数，那么我们的路线不可能触碰到 $y=-1$ 这条线。

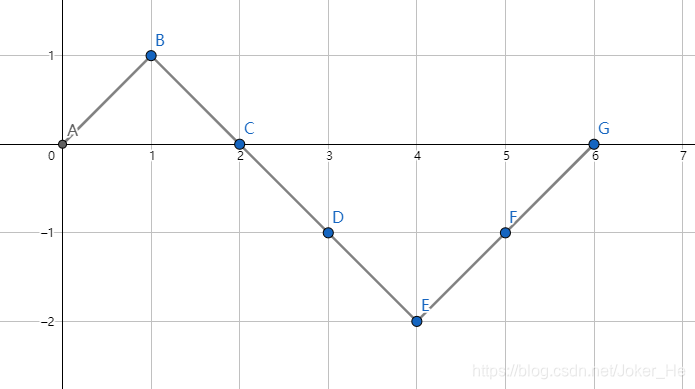
考虑这种走法，我们在第四步碰到了$y=-1$这条线，我们在这里对后面的所有点以$y=-1$为对称轴做轴对称，就有下图：

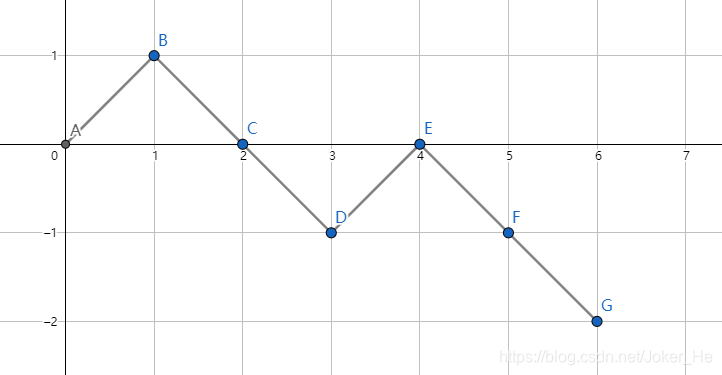
我们最终走到了点$(2n,-2)$，实际上，不论我们中间怎么走，只要在第一次碰到$y=-1$时，对后面的图形做轴对称，终点都是$(2n,-2)$。所以不合法的情况方案数就是$C_{2n}^{n-1}$，即只选了$n-1$次$1$，导致结果走到了$(2n,-2)$。

所以该经典模型的解为：$C_{2n}^n-C_{2n}^{n-1}$。

该模型经典题：P1754球迷购票问题、P1722 矩阵 II、P1976 鸡蛋饼、P1044 栈

卡特兰数扩展模型：

经典模型中，我们需要摆放的$0$和$1$数量是相等的，对此问题稍加扩展，$1$的数量大于$0$的数量，要求任意前缀中$1$的个数不少于$0$的个数。

这个问题我们显然不能再用经典模型推导出来的式子进行计算，但是我们可以借鉴经典模型的推导过程。

这个模型我们最终可以走到$(n+m,n-m)$这个点，我们在第一次触碰到$y=-1$时，也对后续图形做轴对称，我们可以发现，我们最终会走到点$(n+m,m-n-2)$，那么可以知道，当我们选择$m-1$个位置放$1$的时候，会走到这个点，那么此模型的解就是$C_{n+m}^n-C_{n+m}^{m-1}$。

其实经典模型就是扩展模型的一个 $n=m$ 特殊情况。

扩展模型的题：P1641 生成字符串

另外一些题：P3200 有趣的数列、P2532 树屋阶梯