机器学习实战刻意练习-- Task 7 回归

最新推荐文章于 2023-12-11 12:54:44 发布

ZHuZ1H

最新推荐文章于 2023-12-11 12:54:44 发布

阅读量659

点赞数

分类专栏：《机器学习实战》学习文章标签：机器学习 python

本文链接：https://blog.csdn.net/Jupiker/article/details/103618661

版权

《机器学习实战》学习专栏收录该内容

6 篇文章 0 订阅

订阅专栏

Week 5

回归问题（Regression）

回归是对连续型的数据做出处理，回归的目的是预测数值型数据的目标值。
一般是要得出回归方程，求得回归系数的过程就叫做回归。
这一节的回归，都是指的线性回归。

一、用线性回归找到最佳拟合直线

线性回归原理

线性回归和矩阵的求逆

假定输入数据存放在矩阵 x 中，而回归系数存放在向量 w 中。那么对于给定的数据 X1，预测结果将会通过 Y = X1^T w 给出。若给出一些 X 和对应的 y，怎样才能找到 w 呢？一个常用的方法就是找出使误差最小的 w 。这里的误差是指预测 y 值和真实 y 值之间的差值，使用该误差的简单累加将使得正差值和负差值相互抵消，所以我们采用平方误差（实际上就是我们通常所说的最小二乘法）。

平方误差：
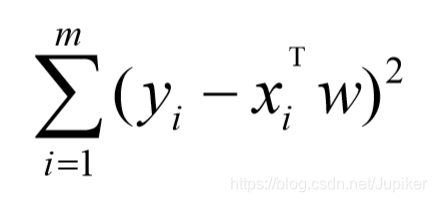
sssss
用矩阵表示：
ssss
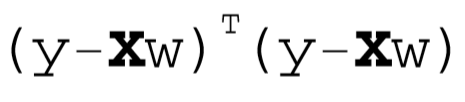
对w求导，得到：
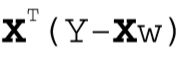
sadasd
最后解出w：
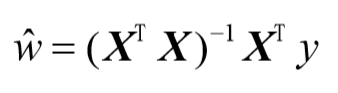
saddsadasd
需要对矩阵求逆，因此这个方程只在逆矩阵存在的时候适用，我们在程序代码中对此作出判断。判断矩阵是否可逆的一个可选方案是:

判断矩阵的行列式是否为 0，若为 0 ，矩阵就不存在逆矩阵，不为 0 的话，矩阵才存在逆矩阵。

最小二乘法

上述的最佳w求解是统计学中的常见问题，除了矩阵方法外还有很多其他方法可以解决。通过调用NumPy库里的矩阵方法，我们可以仅使用几行代码就完成所需功能。该方法也称作 OLS，意思是“普通最小二乘法”（ordinary least squares）。

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。

线性回归工作原理

读入数据，将数据特征x、特征标签y存储在矩阵x、y中
验证 x^Tx 矩阵是否可逆
使用最小二乘法求得 回归系数 w 的最佳估计

线性回归开发流程

收集数据: 采用任意方法收集数据
准备数据: 回归需要数值型数据，标称型数据将被转换成二值型数据
分析数据: 绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后，可以将新拟合线绘在图上作为对比
训练算法: 找到回归系数
测试算法: 使用 R^2 或者预测值和数据的拟合度，来分析模型的效果
使用算法: 使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签

线性回归算法特点

优点：结果易于理解，计算上不复杂。
缺点：对非线性的数据拟合不好。
适用于数据类型：数值型和标称型数据。

线性回归案例示范

下面我们看看实际的效果，看看如何给出数据的最佳拟合直线
我们通过代码来解释：

# 建立 regression.py 文件，并输出下面的代码。（以后的代码都输入到这个文件里，后面就不再复述了）
# 标准回归函数和数据导入函数
from numpy import *
import matplotlib.pylab as plt

def loadDataSet(fileName):
    """ 加载数据
        解析以tab键分隔的文件中的浮点数
    Returns：
        dataMat ：  feature 对应的数据集
        labelMat ： feature 对应的分类标签，即类别标签
    """
    # 获取样本特征的总数，不算最后的目标变量 
    numFeat = len(open(fileName).readline().split('\t')) - 1
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        # 读取每一行
        lineArr = []
        # 删除一行中以tab分隔的数据前后的空白符号
        curLine = line.strip().split('\t')
        # i 从0到2，不包括2 
        for i in range(numFeat):
            # 将数据添加到lineArr List中，每一行数据测试数据组成一个行向量           
            lineArr.append(float(curLine[i]))
            # 将测试数据的输入数据部分存储到dataMat 的List中
        dataMat.append(lineArr)
        # 将每一行的最后一个数据，即类别，或者叫目标变量存储到labelMat List中
        labelMat.append(float(curLine[-1]))
    fr.close()
    return dataMat, labelMat

def standRegres(xArr, yArr):
    '''
    Description：
        线性回归
    Args:
        xArr ：输入的样本数据，包含每个样本数据的 feature
        yArr ：对应于输入数据的类别标签，也就是每个样本对应的目标变量
    Returns:
        ws：回归系数
    '''

    # mat()函数将xArr，yArr转换为矩阵 mat().T 代表的是对矩阵进行转置操作
    xMat = mat(xArr)
    yMat = mat(yArr).T
    # 矩阵乘法的条件是左矩阵的列数等于右矩阵的行数
    xTx = xMat.T * xMat
    # 因为要用到xTx的逆矩阵，所以事先需要确定计算得到的xTx是否可逆，条件是矩阵的行列式不为0
    # linalg.det() 函数是用来求得矩阵的行列式的，如果矩阵的行列式为0，则这个矩阵是不可逆的，就无法进行接下来的运算                   
    if linalg.det(xTx) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return
    # 最小二乘法
    # http://cwiki.apachecn.org/pages/viewpage.action?pageId=5505133
    # 书中的公式，求得w的最优解
    ws = xTx.I * (xMat.T * yMat)
    return ws

# 运行下列命令：
>>> import regression
>>> from numpy import *
>>> xArr, yArr = regression.loadDataSet('data.txt')
# 首先先看前两条数据
>>> xArr[0:2]
[[1.0, 0.067732], [1.0, 0.42781]]
# 第一个值总为1.0，即X0。我们假定偏移量就是一个常数。第二个值X1。
>>> ws = regression.standRegres(xArr, yArr)
>>> ws
matrix([[3.00774324],
        [1.69532264]])
# 变量ws存放的就是回归系数。
>>> xMat = mat(xArr)
>>> yMat = mat(yArr)
>>> yHat = xMat*ws
# 下面就是绘出数据集散点图和最佳拟合直线图
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.scatter(xMat[:,1].flatten().A[0], yMat.T[:,0].flatten().A[0])
<matplotlib.collections.PathCollection object at 0x0000014FE662C208>
# 上述命令创建了图像并绘出了原始的数据。为了绘制计算出的佳拟合直线，需要绘出yHat 的值。如果直线上的数据点次序混乱，绘图时将会出现问题，所以首先要将点按照升序排列
>>> xCopy = xMat.copy()
>>> xCopy.sort(0)
>>> yHat = xCopy*ws
>>> ax.plot(xCopy[:,1],yHat)
[<matplotlib.lines.Line2D object at 0x0000014FE3A1AE48>]
>>> plt.show()
>>> 
# 输出图像如下:

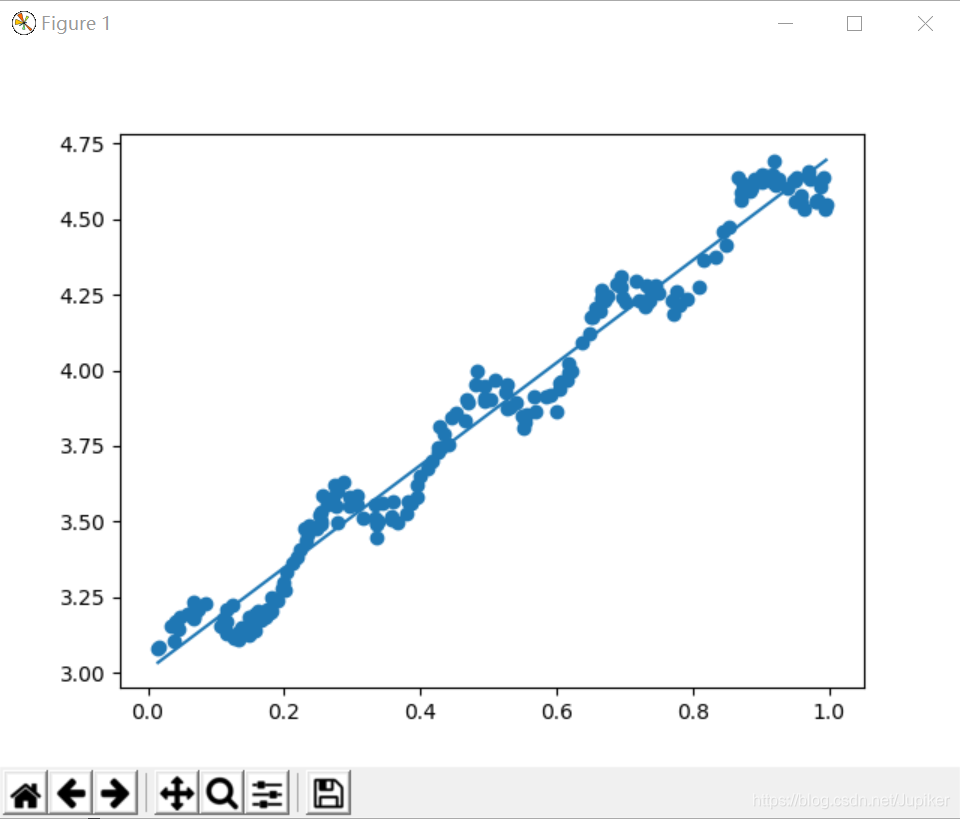
tuxiang

# 可以通过命令corrcoef(yEstimate, yActual)来计算预测值和真实值的相关性。
# 运行下面命令：
# 首先计算出y的预测值yMat
>>> yHat = xMat*ws
# 再来计算相关系数（这时需要将yMat转置，以保证两个向量都是行向量
>>> corrcoef(yHat.T, yMat)
array([[1.        , 0.98647356],
       [0.98647356, 1.        ]])
>>> 
# 该矩阵包含所有两两组合的相关系数。
# 可以看到，对角线上的数据是1.0，因为yMat和自己的匹 配是完美的，而YHat和yMat的相关系数为0.98。

二、局部加权线性回归

线性回归有一个一个问题是有可能出现欠拟合现象，因为它求的是具有最小均方差的无偏估计。所以有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。

一个方法是局部加权线性回归（Locally Weighted Linear Regression，LWLR）。在这个算法中，我们给预测点附近的每个点赋予一定的权重，然后与线性回归类似，在这个子集上基于最小均方误差来进行普通的回归。

回归系数w的形式为：
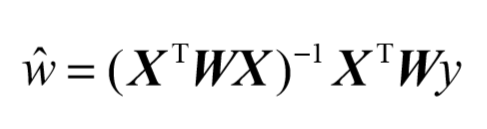
huigui
其中w是一个矩阵，用来给每个数据点赋予权重。

LWLR 使用“核”（与支持向量机中的核类似）来对附近的点赋予更高的权重①。核的类型可以自由选择，常用的核就是高斯核，高斯核对应的权重如下：
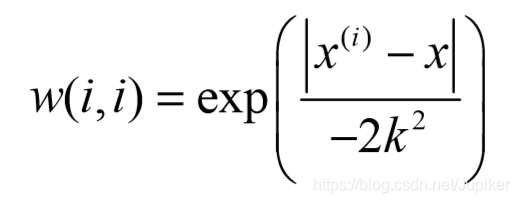
aaaaaa
这样就构建了一个只含对角元素的权重矩阵 w，并且点 x 与 x(i) 越近，w(i) 将会越大。上述公式中包含一个需要用户指定的参数 k ，它决定了对附近的点赋予多大的权重，这也是使用 LWLR 时唯一需要考虑的参数。

局部加权线性回归工作原理

读入数据，将数据特征x、特征标签y存储在矩阵x、y中
利用高斯核构造一个权重矩阵 W，对预测点附近的点施加权重
验证 X^TWX 矩阵是否可逆
使用最小二乘法求得 回归系数 w 的最佳估计

局部加权线性回归项目实例

下面看看模型的效果，代码如下：

# 局部加权线性回归函数
def lwlr(testPoint, xArr, yArr, k=1.0):
    '''
        Description：
            局部加权线性回归，在待预测点附近的每个点赋予一定的权重，在子集上基于最小均方差来进行普通的回归。
        Args：
            testPoint：样本点
            xArr：样本的特征数据，即 feature
            yArr：每个样本对应的类别标签，即目标变量
            k:关于赋予权重矩阵的核的一个参数，与权重的衰减速率有关
        Returns:
            testPoint * ws：数据点与具有权重的系数相乘得到的预测点
        Notes:
            这其中会用到计算权重的公式，w = e^((x^((i))-x) / -2k^2)
            理解：x为某个预测点，x^((i))为样本点，样本点距离预测点越近，贡献的误差越大（权值越大），越远则贡献的误差越小（权值越小）。
            关于预测点的选取，在我的代码中取的是样本点。其中k是带宽参数，控制w（钟形函数）的宽窄程度，类似于高斯函数的标准差。
            算法思路：假设预测点取样本点中的第i个样本点（共m个样本点），遍历1到m个样本点（含第i个），算出每一个样本点与预测点的距离，
            也就可以计算出每个样本贡献误差的权值，可以看出w是一个有m个元素的向量（写成对角阵形式）。
    '''
    # mat() 函数是将array转换为矩阵的函数， mat().T 是转换为矩阵之后，再进行转置操作
    xMat = mat(xArr)
    yMat = mat(yArr).T
    # 获得xMat矩阵的行数
    m = shape(xMat)[0]
    # eye()返回一个对角线元素为1，其他元素为0的二维数组，创建权重矩阵weights，该矩阵为每个样本点初始化了一个权重                   
    weights = mat(eye((m)))
    for j in range(m):
        # testPoint 的形式是 一个行向量的形式
        # 计算 testPoint 与输入样本点之间的距离，然后下面计算出每个样本贡献误差的权值
        diffMat = testPoint - xMat[j, :]
        # k控制衰减的速度
        weights[j, j] = exp(diffMat * diffMat.T / (-2.0 * k**2))
    # 根据矩阵乘法计算 xTx ，其中的 weights 矩阵是样本点对应的权重矩阵
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return
    # 计算出回归系数的一个估计
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

def lwlrTest(testArr, xArr, yArr, k=1.0):
    '''
        Description：
            测试局部加权线性回归，对数据集中每个点调用 lwlr() 函数
        Args：
            testArr：测试所用的所有样本点
            xArr：样本的特征数据，即 feature
            yArr：每个样本对应的类别标签，即目标变量
            k：控制核函数的衰减速率
        Returns：
            yHat：预测点的估计值
    '''
    # 得到样本点的总数
    m = shape(testArr)[0]
    # 构建一个全部都是 0 的 1 * m 的矩阵
    yHat = zeros(m)
    # 循环所有的数据点，并将lwlr运用于所有的数据点 
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    # 返回估计值
    return yHat

# 运行下列命令：
>>> import regression
>>> import importlib
>>> importlib.reload(regression)
<module 'regression' from 'C:\\Users\\dell\\Desktop\\机器学习实战学习资料\\第8章 回归regression\\regression.py'>
# 重新载入数据集
>>> xArr, yArr = regression.loadDataSet('data.txt')
# 对单点进行估计
>>> yArr[0]
3.176513
>>> regression.lwlr(xArr[0], xArr, yArr, 1.0)
matrix([[3.12204471]])
>>> regression.lwlr(xArr[0], xArr, yArr, 0.001)
matrix([[3.20175729]])
# 为了得到数据集里所有点的估计，可以调用lwlrTest()函数：
>>> yHat = regression.lwlrTest(xArr, xArr, yArr, 0.003)
# 下面绘出这些估计值和原始值，看看yHat的拟合效果。所用的绘图函数需要将数据点按序 排列，首先对xArr排序
>>> xMat = mat(xArr)
>>> srtInd = xMat[:,1].argsort(0)
>>> xSort = xMat[srtInd][:,0,:]
# 然后用Matplotlib绘图
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(xSort[:,1], yHat[srtInd])
[<matplotlib.lines.Line2D object at 0x00000216ECD9D470>]
>>> ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0] , s=2)
<matplotlib.collections.PathCollection object at 0x00000216ECD61080>
>>> plt.show()
>>> 
# 输出图像如下：

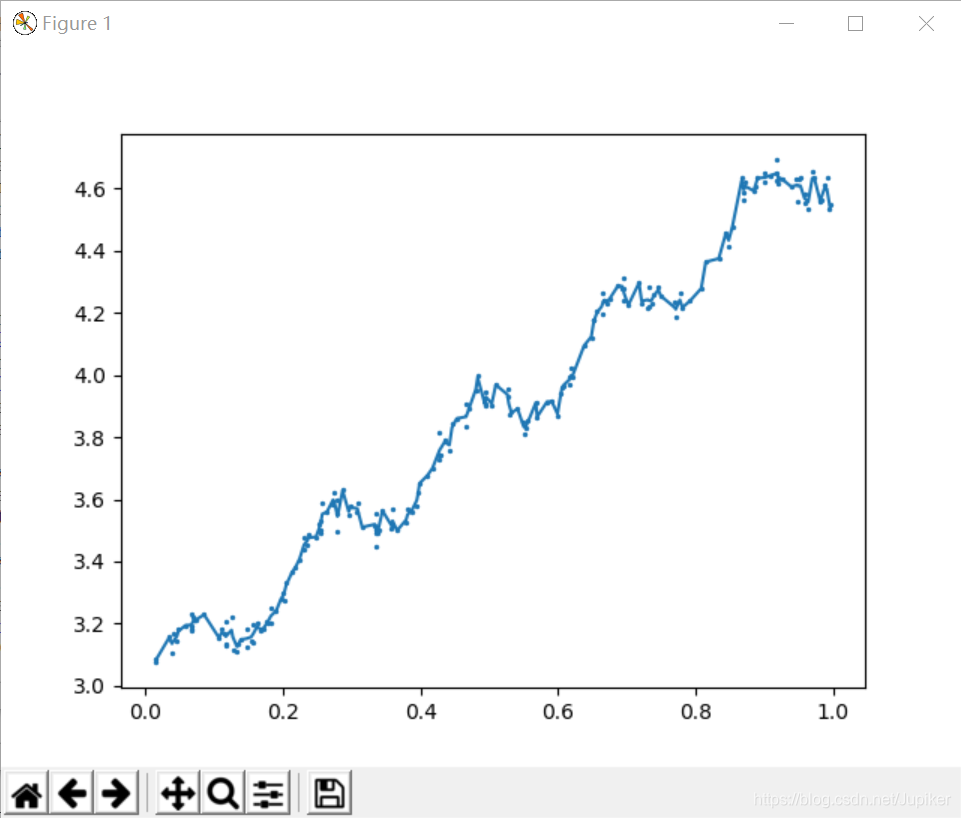
ooppp

三、综合示例：预测鲍鱼的年龄

下面我们回归一组真实数据，代码如下：

# 在这之前，先加入下面的代码到文件中
def rssError(yArr, yHatArr):
    '''
        Desc:
            计算分析预测误差的大小
        Args:
            yArr：真实的目标变量
            yHatArr：预测得到的估计值
        Returns:
            计算真实值和估计值得到的值的平方和作为最后的返回值
    '''
    return ((yArr - yHatArr)**2).sum()

# 运行下列命令：
>>> import regression
>>> import importlib
>>> importlib.reload(regression)
<module 'regression' from 'C:\\Users\\dell\\Desktop\\机器学习实战学习资料\\第8章 回归regression\\regression.py'>
>>> abX, abY = regression.loadDataSet('abalone.txt')
>>> yHat01 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
>>> yHat1 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1)
>>> yHat10 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
# 为了分析预测误差的大小，可以用函数rssError()计算出这一指标
>>> regression.rssError(abY[0:99], yHat01.T)
56.78868743050092
>>> regression.rssError(abY[0:99], yHat1.T)
429.89056187038
>>> regression.rssError(abY[0:99], yHat10.T)
549.1181708827924
# 可以看到，使用较小的核将得到较低的误差。
# 因为使用小的核将造成过拟合，对新数据不一定能达到好的预测效果。
# 下面就来看看它们在新数据上的表现：
>>> yHat01 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
>>> regression.rssError(abY[100:199], yHat01.T)
57913.51550155911
>>> yHat1 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1)
>>> regression.rssError(abY[100:199], yHat1.T)
573.5261441895982
>>> yHat10 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
>>> regression.rssError(abY[100:199], yHat10.T)
517.5711905381903
# 从上述结果可以看到，在上面的三个参数中，核大小等于10时的测试误差小，但它在训练 集上的误差却是大的。
# 接下来再来和简单的线性回归做个比较
>>> ws = regression.standRegres(abX[0:99], abY[0:99])
>>> yHat = mat(abX[100:199])*ws
>>> regression.rssError(abY[100:199], yHat.T.A)
518.6363153245542
>>> 
# 简单线性回归达到了与局部加权线性回归类似的效果

四、缩减系数来“理解”数据

如果特征比样本点还多(n > m)，也就是说输入数据的矩阵 x 不是满秩矩阵。非满秩矩阵求逆时会出现问题。
为了解决这个问题，我们引入了 岭回归（ridge regression） 这种缩减方法。接着是 lasso法，最后介绍 前向逐步回归。

岭回归

岭回归就是在矩阵 X^ TX 上加一个 λI 从而使得矩阵非奇异，进而能对 X^ T+λI 求逆。其中矩阵I是一个 n * n（等于列数）的单位矩阵，对角线上元素全为1，其他元素全为0。此时回归系数w的计算公式为：
sjsjsjssj
这里通过引入 λ 来限制了所有 w 之和，通过引入该惩罚项，能够减少不重要的参数，这个技术在统计学中也叫作缩减(shrinkage)。

缩减方法可以去掉不重要的参数，因此能更好地理解数据。此外，与简单的线性回归相比，缩减法能取得更好的预测效果。

这里通过预测误差最小化得到 λ: 数据获取之后，首先抽一部分数据用于测试，剩余的作为训练集用于训练参数 w。训练完毕后在测试集上测试预测性能。通过选取不同的 λ 来重复上述测试过程，最终得到一个使预测误差最小的 λ 。

下面用代码实现岭回归：

# 岭回归
def ridgeRegres(xMat, yMat, lam=0.2):
    '''
        Desc：
            这个函数实现了给定 lambda 下的岭回归求解。
            如果数据的特征比样本点还多，就不能再使用上面介绍的的线性回归和局部线性回归了，因为计算 (xTx)^(-1)会出现错误。
            如果特征比样本点还多（n > m），也就是说，输入数据的矩阵x不是满秩矩阵。非满秩矩阵在求逆时会出现问题。
            为了解决这个问题，我们下边讲一下：岭回归，这是我们要讲的第一种缩减方法。
        Args：
            xMat：样本的特征数据，即 feature
            yMat：每个样本对应的类别标签，即目标变量，实际值
            lam：引入的一个λ值，使得矩阵非奇异
        Returns：
            经过岭回归公式计算得到的回归系数
    '''

    xTx = xMat.T * xMat
    # 岭回归就是在矩阵 xTx 上加一个 λI 从而使得矩阵非奇异，进而能对 xTx + λI 求逆
    denom = xTx + eye(shape(xMat)[1]) * lam
    # 检查行列式是否为零，即矩阵是否可逆，行列式为0的话就不可逆，不为0的话就是可逆。
    if linalg.det(denom) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return
    ws = denom.I * (xMat.T * yMat)
    return ws

def ridgeTest(xArr, yArr):
    '''
        Desc：
            函数 ridgeTest() 用于在一组 λ 上测试结果
        Args：
            xArr：样本数据的特征，即 feature
            yArr：样本数据的类别标签，即真实数据
        Returns：
            wMat：将所有的回归系数输出到一个矩阵并返回
    '''

    xMat = mat(xArr)
    yMat = mat(yArr).T
    # 计算Y的均值
    yMean = mean(yMat, 0)
    # Y的所有的特征减去均值
    yMat = yMat - yMean
    # 标准化 x，计算 xMat 平均值
    xMeans = mean(xMat, 0)
    # 然后计算 X的方差
    xVar = var(xMat, 0)
    # 所有特征都减去各自的均值并除以方差
    xMat = (xMat - xMeans) / xVar
    # 可以在 30 个不同的 lambda 下调用 ridgeRegres() 函数。
    numTestPts = 30
    # 创建30 * m 的全部数据为0 的矩阵
    wMat = zeros((numTestPts, shape(xMat)[1]))
    for i in range(numTestPts):
        # exp() 返回 e^x 
        ws = ridgeRegres(xMat, yMat, exp(i - 10))
        wMat[i, :] = ws.T
    return wMat

# 运行下列命令：
>>> import regression
>>> import importlib
>>> importlib.reload(regression)
<module 'regression' from 'C:\\Users\\dell\\Desktop\\机器学习实战学习资料\\第8章 回归regression\\regression.py'>
>>> abX, abY =regression.loadDataSet('abalone.txt')
>>> ridgeWeights = regression.ridgeTest(abX, abY)
# 这样就得到了30个不同lambda所对应的回归系数。为了看到缩减的效果
# 下面开始绘图
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(ridgeWeights)
[<matplotlib.lines.Line2D object at 0x0000020D03C78710>, <matplotlib.lines.Line2D object at 0x0000020D03C78860>, <matplotlib.lines.Line2D object at 0x0000020D03C789B0>, <matplotlib.lines.Line2D object at 0x0000020D03C78B00>, <matplotlib.lines.Line2D object at 0x0000020D03C78C50>, <matplotlib.lines.Line2D object at 0x0000020D03C78DA0>, <matplotlib.lines.Line2D object at 0x0000020D03C78EF0>, <matplotlib.lines.Line2D object at 0x0000020D03C86080>]
>>> plt.show()
>>> 
# 输出图像如下：

ashfaosknvlkcn
上图绘制出了回归系数与 log(λ) 的关系。在最左边，即 λ 最小时，可以得到所有系数的原始值（与线性回归一致）；而在右边，系数全部缩减为0；在中间部分的某值将可以取得最好的预测效果。为了定量地找到最佳参数值，还需要进行交叉验证。

套索方法(Lasso，The Least Absolute Shrinkage and Selection Operator)

在增加如下约束时，普通的最小二乘法回归会得到与岭回归一样的公式:
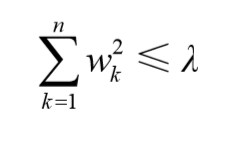
sadasdasdad
上式限定了所有回归系数的平方和不能大于 λ 。正是因为上述限制，使用岭回归可以避免。与岭回归类似，另一个缩减方法lasso也对回归系数做了限定，对应的约束条件如下:
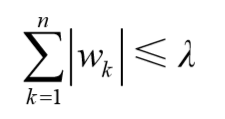
qwrqfewwfaes
唯一的不同点在于，这个约束条件使用绝对值取代了平方和。虽然约束形式只是稍作变化，结果却大相径庭: 在 λ 足够小的时候，一些系数会因此被迫缩减到 0.这个特性可以帮助我们更好地理解数据。

前向逐步回归

前向逐步回归算法可以得到与 lasso 差不多的效果，但更加简单。它每一步都尽可能减少误差。一开始，所有权重都设置为 0，然后每一步所做的决策是对某个权重增加或减少一个很小的值。

给出伪代码：

数据标准化，使其分布满足 0 均值 和单位方差
在每轮迭代过程中: 
    设置当前最小误差 lowestError 为正无穷
    对每个特征:
        增大或缩小:
            改变一个系数得到一个新的 w
            计算新 w 下的误差
            如果误差 Error 小于当前最小误差 lowestError: 设置 Wbest 等于当前的 W
        将 W 设置为新的 Wbest

下面用代码实现该回归：

# 辅助函数
def regularize(xMat):  # 按列进行规范化
    inMat = xMat.copy()
    inMeans = mean(inMat, 0)  # 计算平均值然后减去它
    inVar = var(inMat, 0)  # 计算除以Xi的方差
    inMat = (inMat - inMeans) / inVar
    return inMat
    
# 前向逐步线性回归
def stageWise(xArr, yArr, eps=0.01, numIt=100):
    """
    前向逐步线性回归
    - - - -
    xArr - x输入数据

    yArr - y预测数据

    eps - 每次迭代需要调整的步长

    numIt - 迭代次数
    """
    #数据初始化、标准化
    xMat = mat(xArr)
    yMat = mat(yArr).T
    yMean = mean(yMat, 0)
    yMat = yMat - yMean  # 也可以规则化ys但会得到更小的coef
    xMat = regularize(xMat)
    m, n = shape(xMat)
    returnMat = zeros((numIt,n)) # 测试代码删除
    ws = zeros((n, 1))
    wsTest = ws.copy()
    wsMax = ws.copy()
    #迭代numIt次
    for i in range(numIt):
        print(ws.T)
        lowestError = inf
        #遍历每个特征的回归系数
        for j in range(n):
            for sign in [-1, 1]:
                wsTest = ws.copy()
                #微调回归系数
                wsTest[j] += eps * sign
                #计算预测值
                yTest = xMat * wsTest
                #计算平方误差
                rssE = rssError(yMat.A, yTest.A)
                #如果误差更小，则更新当前的最佳回归系数
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        #记录numIt次迭代的回归系数矩阵
        returnMat[i,:]=ws.T
    return returnMat

# 运行下列命令：
 ==
>>> import regression
>>> import importlib
>>> importlib.reload(regression)
<module 'regression' from 'C:\\Users\\dell\\Desktop\\机器学习实战学习资料\\第8章 回归regression\\regression.py'>
>>> xArr, yArr = regression.loadDataSet('abalone.txt')
>>> regression.stageWise(xArr, yArr, 0.01, 200)
[[0. 0. 0. 0. 0. 0. 0. 0.]]
[[0.   0.   0.   0.01 0.   0.   0.   0.  ]]
.......(省略)
[[ 0.05  0.    0.09  0.03  0.31 -0.64  0.    0.36]]
[[ 0.04  0.    0.09  0.03  0.31 -0.64  0.    0.36]]
array([[ 0.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
       ...,
       [ 0.05,  0.  ,  0.09, ..., -0.64,  0.  ,  0.36],
       [ 0.04,  0.  ,  0.09, ..., -0.64,  0.  ,  0.36],
       [ 0.05,  0.  ,  0.09, ..., -0.64,  0.  ,  0.36]])
# 上述结果中值得注意的是w1和w6都是0，这表明它们不对目标值造成任何影响，也就是说这 些特征很可能是不需要的。
# 在参数eps设置为0.01的情况下，一段时间后系数就已经饱和 并在特定值之间来回震荡，这是因为步长太大的缘故。
# 下面试着用更小的步长和更多的步数： 
>>> regression.stageWise(xArr, yArr, 0.001, 5000)
[[0. 0. 0. 0. 0. 0. 0. 0.]]
[[0.    0.    0.    0.001 0.    0.    0.    0.   ]]
........
[[ 0.043 -0.011  0.12   0.022  2.023 -0.963 -0.105  0.187]]
[[ 0.044 -0.011  0.12   0.022  2.023 -0.963 -0.105  0.187]]
array([[ 0.   ,  0.   ,  0.   , ...,  0.   ,  0.   ,  0.   ],
       [ 0.   ,  0.   ,  0.   , ...,  0.   ,  0.   ,  0.   ],
       [ 0.   ,  0.   ,  0.   , ...,  0.   ,  0.   ,  0.   ],
       ...,
       [ 0.043, -0.011,  0.12 , ..., -0.963, -0.105,  0.187],
       [ 0.044, -0.011,  0.12 , ..., -0.963, -0.105,  0.187],
       [ 0.043, -0.011,  0.12 , ..., -0.963, -0.105,  0.187]])
# 接下来把这些结果与小二乘法进行比较，后者的结果可以通过如下代码获得：
>>> xMat = mat(xArr)
>>> yMat = mat(yArr).T
>>> xMat = regression.regularize(xMat)
>>> yM = mean(yMat, 0)
>>> yMat = yMat - yM
>>> weights = regression.standRegres(xMat, yMat.T)
>>> weights.T
matrix([[ 0.0430442 , -0.02274163,  0.13214087,  0.02075182,  2.22403814,
         -0.99895312, -0.11725427,  0.16622915]])

五、权衡偏差与方差

任何时候，一旦发现模型和测量值之间存在差异，就说出现了误差。当考虑模型中的“噪声” 或者说误差时，必须考虑其来源。

下面给出了训练误差和测试误差的曲线图，上面的曲线就是测试误差，下面的曲线是训练误差。根据上面讲过的我们知道：如果降低核的大小，那么训练误差将变小。从下图来看，从左到右就表示了核逐渐减小的过程。
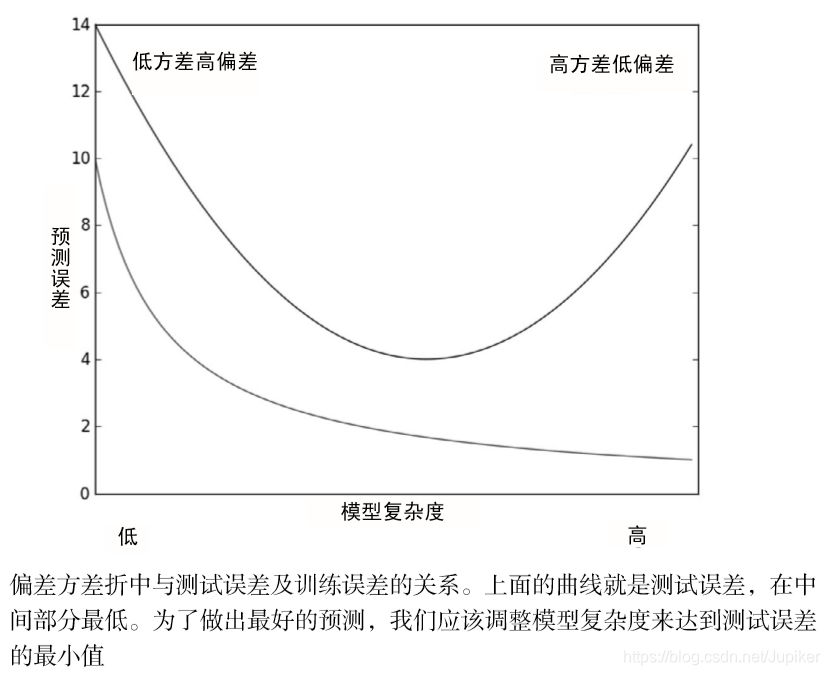
sadavtbhfrhtg
一般认为，上述两种误差由三个部分组成：偏差、测量误差和随机噪声
局部加权线性回归 和 预测鲍鱼年龄 中，我们通过引入了三个越来越小的核来不断增大模型的方差。

方差是可以度量的。如果从鲍鱼数据中取一个随机样本集（例如取其中 100 个数据）并用线性模型拟合，将会得到一组回归系数。同理，再取出另一组随机样本集并拟合，将会得到另一组回归系数。这些系数间的差异大小也就是模型方差的反映。

六、综合示例：预测乐高玩具套装的价格

下面给出一个预测模型：

(1) 收集数据：用 Google Shopping 的API收集数据。
(2) 准备数据：从返回的JSON数据中抽取价格。
(3) 分析数据：可视化并观察数据。
(4) 训练算法：构建不同的模型，采用逐步线性回归和直接的线性回归模型。
(5) 测试算法：使用交叉验证来测试不同的模型，分析哪个效果最好。
(6) 使用算法：这次练习的目标就是生成数据模型。

代码实现：

'''
———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
下面是书上的方法（但是因为某些原因没法运行命令，所以在后面我从网上找到了另外一种方法来运行）
有些模块如果没有的话需要自己安装，我是通过pip安装的。
'''
from time import sleep
import json
from urllib.request import urlopen

def searchForSet(retX, retY, setNum, yr, numPce, origPrc):
    sleep(10)
    myAPIstr = 'AIzaSyD2cR2KFyx12hXu6PFU-wrWot3NXvko8vY'
    searchURL = 'https://www.googleapis.com/shopping/search/v1/public/products?key=%s&country=US&q=lego+%d&alt=json' % (myAPIstr, setNum)
    pg = urlopen(searchURL)
    retDict = json.loads(pg.read())
    for i in range(len(retDict['items'])):
        try:
            currItem = retDict['items'][i]
            if currItem['product']['condition'] == 'new':
                newFlag = 1
            else: newFlag = 0
            listOfInv = currItem['product']['inventories']
            for item in listOfInv:
                sellingPrice = item['price']
                if  sellingPrice > origPrc * 0.5:
                    print ("%d\t%d\t%d\t%f\t%f" % (yr,numPce,newFlag,origPrc, sellingPrice))
                    retX.append([yr, numPce, newFlag, origPrc])
                    retY.append(sellingPrice)
        except: print ('problem with item %d' % i)
        
def setDataCollect(retX, retY):
    searchForSet(retX, retY, 8288, 2006, 800, 49.99)
    searchForSet(retX, retY, 10030, 2002, 3096, 269.99)
    searchForSet(retX, retY, 10179, 2007, 5195, 499.99)
    searchForSet(retX, retY, 10181, 2007, 3428, 199.99)
    searchForSet(retX, retY, 10189, 2008, 5922, 299.99)
    searchForSet(retX, retY, 10196, 2009, 3263, 249.99)

'''
————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
网上寻找的方法（可以运行，但是还是有小毛病我还没解决）
'''
from numpy import *
from bs4 import BeautifulSoup

# 从页面读取数据，生成retX和retY列表
def scrapePage(retX, retY, inFile, yr, numPce, origPrc):
    """
    从页面读取数据，生成retX和retY列表
    retX - 数据X

    retY - 数据Y

    inFile - HTML文件

    yr - 年份

    numPce - 乐高部件数目

    origPrc - 原价
    """

    # 打开并读取HTML文件
    with open(inFile, encoding = 'utf-8') as f:
        html = f.read()
    soup = BeautifulSoup(html)
    i=1
    # 根据HTML页面结构进行解析
    currentRow = soup.findAll('table', r="%d" % i)
    while(len(currentRow)!=0):
        currentRow = soup.findAll('table', r="%d" % i)
        title = currentRow[0].findAll('a')[1].text
        lwrTitle = title.lower()
        # 查找是否有全新标签
        if (lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1):
            newFlag = 1.0
        else:
            newFlag = 0.0
        # 查找是否已经标志出售，我们只收集已出售的数据
        soldUnicde = currentRow[0].findAll('td')[3].findAll('span')
        if len(soldUnicde)==0:
            print("item #%d did not sell" % i)
        else:
            # 解析页面获取当前价格
            soldPrice = currentRow[0].findAll('td')[4]
            priceStr = soldPrice.text
            priceStr = priceStr.replace('$','') #strips out $
            priceStr = priceStr.replace(',','') #strips out ,
            if len(soldPrice)>1:
                priceStr = priceStr.replace('Free shipping', '')
            sellingPrice = float(priceStr)
            # 去掉不完整的套装价格
            if  sellingPrice > origPrc * 0.5:
                    # print("%d\t%d\t%d\t%f\t%f" % (yr,numPce,newFlag,origPrc, sellingPrice))
                    retX.append([yr, numPce, newFlag, origPrc])
                    retY.append(sellingPrice)
        i += 1
        currentRow = soup.findAll('table', r="%d" % i)
        
# 依次读取六种乐高套装的数据，并生成数据矩阵        
def setDataCollect(retX, retY):
    scrapePage(retX, retY, 'setHtml/lego8288.html', 2006, 800, 49.99)
    scrapePage(retX, retY, 'setHtml/lego10030.html', 2002, 3096, 269.99)
    scrapePage(retX, retY, 'setHtml/lego10179.html', 2007, 5195, 499.99)
    scrapePage(retX, retY, 'setHtml/lego10181.html', 2007, 3428, 199.99)
    scrapePage(retX, retY, 'setHtml/lego10189.html', 2008, 5922, 299.99)
    scrapePage(retX, retY, 'setHtml/lego10196.html', 2009, 3263, 249.99)

# 运行下列命令：
>>> import regression
>>> lgX = [];lgY = []
>>> regression.setDataCollect(lgX,lgY)
'''这里出现了问题
Warning (from warnings module):
  File "C:\Users\dell\Desktop\机器学习实战学习资料\第8章 回归regression\regression.py", line 327
    soup = BeautifulSoup(html)
UserWarning: No parser was explicitly specified, so I'm using the best available HTML parser for this system ("html.parser"). This usually isn't a problem, but if you run this code on another system, or in a different virtual environment, it may use a different parser and behave differently.
'''
The code that caused this warning is on line 327 of the file C:\Users\dell\Desktop\机器学习实战学习资料\第8章 回归regression\regression.py. To get rid of this warning, pass the additional argument 'features="html.parser"' to the BeautifulSoup constructor.

2006	800	0	49.990000	85.000000
2006	800	0	49.990000	102.500000
2006	800	0	49.990000	77.000000
item #4 did not sell
2006	800	0	49.990000	162.500000
.......
2009	3263	0	249.990000	399.950000
item #12 did not sell
2009	3263	1	249.990000	331.510000
>>> 
# 训练算法：建立模型
# 首先需要添加对应常数项的特征X0（X0=1），为此创建一个全1的矩阵： 
>>> shape(lgX)
(63, 4)
>>> lgX1 = mat(ones((63, 5)))
# 将原数据矩阵lgX复制到新数据矩阵lgX1的第1到第5列： 
>>> lgX1[:,1:5] = mat(lgX)
# 确认一下数据复制的正确性： 
>>> lgX[0]
[2006, 800, 0.0, 49.99]
>>> lgX1[0]
matrix([[1.000e+00, 2.006e+03, 8.000e+02, 0.000e+00, 4.999e+01]])
# 很显然，后者除了在第0列加入1之外其他数据都一样。最后在这个新数据集上进行回归处理：
>>> ws = regression.standRegres(lgX1, lgY)
>>> ws
matrix([[ 5.53199701e+04],
        [-2.75928219e+01],
        [-2.68392234e-02],
        [-1.12208481e+01],
        [ 2.57604055e+00]])
# 检查一下结果，看看模型是否有效
>>> lgX1[0]*ws
matrix([[76.07418864]])
>>> lgX1[-1]*ws
matrix([[431.17797682]])
>>> lgX1[43]*ws
matrix([[516.20733116]])
>>> 

# 这个模型本身并不能令人满意。它对于数据拟合得很好，但从公式看，套装里零部件越多售价反而会越低。
# 下面使用缩减法中一种，即岭回归再进行一次实验。前面讨论过如何对系数进行缩减，但这 次将会看到如何用缩减法确定最佳回归系数。
# 交叉验证测试岭回归
def crossValidation(xArr,yArr,numVal=10):
    # 获得数据点个数，xArr和yArr具有相同长度
    m = len(yArr)
    indexList = list(range(m))
    errorMat = zeros((numVal,30))
    # 主循环 交叉验证循环
    for i in range(numVal):
        # 随机拆分数据，将数据分为训练集（90%）和测试集（10%）
        trainX=[]; trainY=[]
        testX = []; testY = []
        # 对数据进行混洗操作
        random.shuffle(indexList)
        # 切分训练集和测试集
        for j in range(m):
            if j < m*0.9: 
                trainX.append(xArr[indexList[j]])
                trainY.append(yArr[indexList[j]])
            else:
                testX.append(xArr[indexList[j]])
                testY.append(yArr[indexList[j]])
        # 获得回归系数矩阵
        wMat = ridgeTest(trainX,trainY)
        # 循环遍历矩阵中的30组回归系数
        for k in range(30):
            # 读取训练集和数据集
            matTestX = mat(testX); matTrainX=mat(trainX)
            # 对数据进行标准化
            meanTrain = mean(matTrainX,0)
            varTrain = var(matTrainX,0)
            matTestX = (matTestX-meanTrain)/varTrain
            # 测试回归效果并存储
            yEst = matTestX * mat(wMat[k,:]).T + mean(trainY)
            # 计算误差
            errorMat[i,k] = ((yEst.T.A-array(testY))**2).sum()
    # 计算误差估计值的均值
    meanErrors = mean(errorMat,0)
    minMean = float(min(meanErrors))
    bestWeights = wMat[nonzero(meanErrors==minMean)]
    # 不要使用标准化的数据，需要对数据进行还原来得到输出结果
    xMat = mat(xArr); yMat=mat(yArr).T
    meanX = mean(xMat,0); varX = var(xMat,0)
    unReg = bestWeights/varX
    # 输出构建的模型
    print("the best model from Ridge Regression is:\n",unReg)
    print("with constant term: ",-1*sum(multiply(meanX,unReg)) + mean(yMat))

# 运行下列命令：
>>> regression.crossValidation(lgX, lgY, 10)
the best model from Ridge Regression is:
 [[-3.24368232e+01  3.16677986e-04 -2.39999025e+01  2.08973635e+00]]
with constant term:  65092.11538341208
# 我们来看一下在缩减过程中回归系数是如何变化的
>>> regression.ridgeTest(lgX, lgY)
array([[-1.45288906e+02, -8.39360442e+03, -3.28682450e+00,
         4.42362406e+04],
       .......,
       [-4.91045279e-06,  5.01149871e-08,  2.40728171e-05,
         8.14042912e-07]])
>>> 
# 这些系数是经过不同程度的缩减得到的
# 这种分析方法使得我们可以挖掘大量数据的内在规律：在仅有4个特征时，该方法的效果也 许并不明显；但如果有100个以上的特征，该方法就会变得十分有效。
# 它可以指出哪些特征是关 键的，而哪些特征是不重要的。

备注：

学习参考资料：
《机器学习实战》
https://github.com/apachecn/AiLearning/blob/master/docs/ml/8.%E5%9B%9E%E5%BD%92.md
https://blog.csdn.net/nanashi_F/article/details/103532815
https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/8.Regression/regression.py#L337
https://github.com/TrWestdoor/Machine-Learning-in-Action/blob/master/sec8-regression/regression.py#L12

ZHuZ1H

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
机器学习实战刻意练习-- Task 7 回归

Week 5回归问题（Regression）回归是对连续型的数据做出处理，回归的目的是预测数值型数据的目标值。一般是要得出回归方程，求得回归系数的过程就叫做回归。这一节的回归，都是指的线性回归。一、用线性回归找到最佳拟合直线线性回归原理线性回归和矩阵的求逆假定输入数据存放在矩阵 x 中，而回归系数存放在向量 w 中。那么对于给定的数据 X1，预测结果将会通过 Y = X1...
复制链接

扫一扫