1.构建方法
二叉树的前序、中序和后序序列中的任何一个都不能唯一确定一棵二叉树,二叉树的构建主要有两大方法。
第一种是中序序列和前、后,层次序列任一组合唯一确定一颗二叉树。前、后、层次序列用来提供根结点信息,中序序列用来区分左右子树;
第二种是根据二叉树对应的扩充二叉树的前序或者后序序列来确定。注意扩充二叉树的中序遍历序列是不能唯一确定二叉树的结构。反例证明如下:

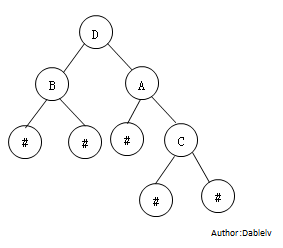
上图中扩展二叉树的中序遍历序列为:#B#D#A#C#,那么也可以对应为下面的扩展二叉树:
2.前序+中序序列构建
构建过程:
(1)根据给定的树写出前序和中序序列;
(2)前序序列中的第一个数字为根结点,构造根结点;
(3)找到根结点在中序序列中的位置,中序中根结点左右两边分别为左子树和右子树的中序序列,根据左右子树结点数量可以在前序序列根节点后面分别找到左子树和右子树的前序序列;
(4)递归处理左右子树,返回根结点,完成构造。
构建过程示例:
以如下二叉树为例:

其前序遍历序列为:{1,2,4,7,3,5,6,8},中序遍历序列为:{4,7,2,1,5,3,8,6}。
根据前序序列找到根结点 1,根据根结点在中序序列中的位置,可以发现有三个左子树结点的值,四个右子树结点值。因此在前序序列中,根节点后面的 3 个数字就是左子树结点的值,再后面的所有数字都是右子树结点值。这样子我们就在前序序列和中序序列中找到了左右子树对应的子序列,然后再递归处理即可。
前序序列:

中序序列:

理解上面的过程,即可根据前序序列和中序序列构建二叉树。二叉树的存储可以用顺序存储(数组)或链式存储,本文采用的就是链式存储。Talk is cheap. Show me the code.
// 二叉树节点结构体
struct BinaryTreeNode {
int m_key;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
BinaryTreeNode() {
m_pLeft = m_pRight = nullptr;
}
};
// @brief: 根据前序序列和中序序列构建二叉树
// @param: preOrder:前序序列; midOrder:中序序列; len:结点数
// @ret: 二叉树根结点
BinaryTreeNode* constructPreMid(int* preOrder, int* midOrder, uint32_t len) {
if(preOrder==nullptr || midOrder==nullptr || len==0) return nullptr;
//先根遍历(前序遍历)的第一个值就是根节点的键值
int rootKey=preOrder[0];
BinaryTreeNode* root=new BinaryTreeNode;
root->m_key=rootKey;
// 只有一个结点
if (len == 1) {
if (*preOrder == *midOrder) {
return root;
} else {
return nullptr;
}
}
// 在中序序列中找到根结点
int* rootMidOrder=midOrder;
// 左子树结点数
int leftLen=0;
while(*rootMidOrder!=rootKey && leftLen < len) {
++rootMidOrder;
++leftLen;
}
// 在中序序列未找到根结点,输入错误
if(*rootMidOrder!=rootKey) return nullptr;
// 构建左子树
if(leftLen>0) {
root->m_pLeft=constructPreMid(preOrder+1, midOrder, leftLen);
}
// 构建右子树
if(len-leftLen-1>0) {
root->m_pRight=constructPreMid(preOrder+leftLen+1, rootMidOrder+1, len-leftLen-1);
}
return root;
}
验证代码:
// @brief: 后根递归遍历
void postorderRecursion(BinaryTreeNode* root) {
if(root==nullptr) return;
postorderRecursion(root->m_pLeft);
postorderRecursion(root->m_pRight);
cout << " " << root->m_key;
}
int main() {
int preorder[] = {1,2,4,7,3,5,6,8};
int midorder[] = {4,7,2,1,5,3,8,6};
BinaryTreeNode* root = constructPreMid(preorder, midorder, 8);
postorderRecursion(root);
}
运行输出:
7,4,2,5,8,6,3,1
3.后序+中序序列构建
这种方法和前面前序+中序序列构建的过程很像,唯一的区别就是对后序序列处理时,所找出的根结点和左右子树的位置不同而已。
还是以上面的二叉树为例,给出构建过程。
(1)根据给定的二叉树,得到后序序列 {7,4,2,5,8,6,3,1} 和中序序列为 {4,7,2,1,5,3,8,6};
(2)后序序列中的最后一个数字为根结点,构造根结点;
(3)找到根结点在中序序列中的位置,中序中根结点左右两边分别为左子树和右子树的中序序列,根据左右子树结点数量可以在后序序列根节点前面分别找到左子树和右子树的后序序列;
(4)递归处理左右子树,返回根结点,完成构造。
后序序列:

中序序列:

Talk is cheap. Show me the code.
// @brief: 根据后序+中序序列构建二叉树
// @ret: 二叉树的根结点
BinaryTreeNode* constructPostMid(int* postorder, int* midorder, uint32_t len) {
// 参数检查
if (postorder == nullptr || midorder == nullptr || len == 0) return nullptr;
// 后序序列的最后一个值是根结点的值
int rootKey = postorder[len - 1];
BinaryTreeNode* root = new BinaryTreeNode;
root->m_key = rootKey;
// 只有一个结点
if (len == 1) {
if (*postorder == *postorder) return root;
else return nullptr;
}
// 在中序序列中找到根结点
int* rootMidorder = midorder;
// 左子树结点数
int leftLen = 0;
while (*rootMidorder != rootKey && leftLen < len) {
++rootMidorder;
++leftLen;
}
// 在中序序列未找到根结点,输入错误
if (*rootMidorder != rootKey) return nullptr;
// 构建左子树
if (leftLen>0) {
root->m_pLeft = constructPostMid(postorder, midorder, leftLen);
}
// 构建右子树
if (len-leftLen-1 > 0) {
root->m_pRight = constructPostMid(postorder + leftLen, rootMidorder + 1, len - leftLen - 1);
}
return root;
}
验证代码:
// @brief: 先根递归遍历
void preorderRecursion(BinaryTreeNode* root) {
if (root == nullptr) return;
cout << " " << root->m_key;
preorderRecursion(root->m_pLeft);
preorderRecursion(root->m_pRight);
}
int main() {
int postorder[] = {7,4,2,5,8,6,3,1};
int midorder[] = {4,7,2,1,5,3,8,6};
BinaryTreeNode* root = constructPostMid(postorder, midorder, 8);
preorderRecursion(root);
}
运行输出:
1 2 4 7 3 5 6 8
4.层次+中序序列构建
“层次+中序”的构建方法同样可以参考前面“前序+中序”和“后序+中序”的方法,可以采用递归的方式来构建。在层次序列中获取子树的层次序列时,和从前序以及后序序列获取子树的前序与后序序列稍有不同,子树的层次序列并非连续,需要根据中序序列中的左右子树从层序序列中提取子树的层次序列,然后递归构建左右子树即可。
还是以上面的二叉树为例,给出构建过程。
(1)根据给定的二叉树,得到层次序列 {1,2,3,4,5,6,7,8} 和中序序列为 {4,7,2,1,5,3,8,6};
(2)层次序列中的第一个数字为根结点,构造根结点;
(3)找到根结点在中序序列中的位置,中序中根结点左右两边分别为左子树和右子树的中序序列。根据左右子树结点值在层次序列中按顺序找到左子树和右子树的层次序列;
(4)递归处理左右子树,返回根结点,完成构造。
层次序列:

中序序列:

Talk is cheap. Show me the code.
// @brief: 根据后序+中序序列构建二叉树
// @ret: 二叉树的根结点
BinaryTreeNode* constructLevelMid(const vector<int>& levelorder, const vector<int>& midorder) {
// 参数检查
if (levelorder.size() == 0 || midorder.size() == 0 || levelorder.size() != midorder.size()) {
return nullptr;
}
// 层次序列的第一个值是根结点
int rootKey = levelorder.front();
BinaryTreeNode* root = new BinaryTreeNode;
root->m_key = rootKey;
// 只有一个结点
if (levelorder.size() == 1) {
if (levelorder.front() == midorder.front()){
return root;
} else {
return nullptr;
}
}
// 在中序序列中找到根结点下标
int index = 0;
while(index < midorder.size()-1 && midorder.at(index)!= rootKey) {
index++;
}
// 从层次序列中找到左子树和右子树的层次序列
vector<int> lLevelorder, rLevelorder;
for (int i = 1; i < levelorder.size(); i++) {
bool isLeft = false;
for (int j = 0; j < index; j++) {
if (levelorder.at(i) == midorder.at(j)) {
isLeft = true;
break;
}
}
if (isLeft) {
lLevelorder.push_back(levelorder.at(i));
} else {
rLevelorder.push_back(levelorder.at(i));
}
}
// 从中序序列找到左子树和右子树的中序序列
vector<int> lMidorder, rMidorder;
for (int i = 0; i < midorder.size(); i++) {
if (i < index){
lMidorder.push_back(midorder.at(i));
} else if (i > index) {
rMidorder.push_back(midorder.at(i));
}
}
// 构建左子树
if (lLevelorder.size() > 0) {
root->m_pLeft=constructLevelMid(lLevelorder, lMidorder);
}
// 构建右子树
if (rLevelorder.size() > 0){
root->m_pRight = constructLevelMid(rLevelorder, rMidorder);
}
return root;
}
验证如下:
int main() {
vector<int> levelorder = { 1,2,3,4,5,6,7,8 };
vector<int> midorder = { 4,7,2,1,5,3,8,6 };
BinaryTreeNode* root = constructLevelMid(levelorder, midorder);
postorderRecursion(root);
}
运行输出:
7 4 2 5 8 6 3 1
5.扩充二叉树前序序列构建
因为扩充二叉树包含空的叶子结点,可以用来判断子树是否为空,因此可以通过扩充二叉树的前序序列唯一构建一颗二叉树。
还是以上面的二叉树为例,扩充结点使用 -1 表示,其扩充二叉树如下:

(1)第一步,获取扩充二叉树的前序序列 { 1, 2, 4, -1, 7, -1, -1, -1, 3, 5, -1, -1, 6, 8, -1, -1, -1};
(2)第二步,前序序列中第一个元素为根结点,紧接着是左子树和右子树的前序序列。如果根结点为 -1 表示扩充结点,返回空结点,否则构建根结点;

(3)第三步,递归处理左子树与右子树。
实现如下:
// @brief: 扩充二叉树前序序列递归构建二叉树
// @para: eBTPreorder:扩充二叉树前序序列
// @ret: 二叉树根结点
BinaryTreeNode* createBTreeEPreorder(int*& eBTPreorder) {
// 扩充结点
if (*eBTPreorder == -1) {
eBTPreorder++;
return nullptr;
}
BinaryTreeNode* root = new BinaryTreeNode;
root->m_key = *eBTPreorder;
++extendedBTPreorder;
root->m_pLeft = createBTree(eBTPreorder);
root->m_pRight = createBTree(eBTPreorder);
return root;
}
验证如下:
int main() {
int* ePreorder = new int[17]{1, 2, 4, -1, 7, -1, -1, -1, 3, 5, -1, -1, 6, 8, -1, -1, -1};
BinaryTreeNode* root = createBTreeEPreorder(ePreorder);
postorderRecursion(root);
}
运行输出:
7 4 2 5 8 6 3 1
注意: 扩充二叉树先根序列使用引用的方式,保证每次生成新结点时指针后移一位。
6.扩充二叉树后序序列构建
通过扩充二叉树后序序列同样可以唯一构建一颗二叉树。还是以上面的二叉树为例,扩充结点使用 -1 表示。
(1)第一步,获取扩充二叉树的后序序列 { -1, -1, -1, 7, 4, -1, 2, -1, -1, 5, -1, -1, 8, -1, 6, 3, 1};
(2)第二步,后序序列从后往前分别是根、右子树的后序序列、左子树的后序序列,以最后一个元素构造根结点;因为是从后序序列的最后一个元素构造根结点,所以后序序列应该采用反序。

(3)第三步,递归构建右子树与左子树。
实现如下:
// @brief: 扩充二叉树后序序列递归构建二叉树
// @para: revEBTPostorder 扩充二叉树后序序列的反序列
// @ret: 二叉树根结点
BinaryTreeNode* createBTreeEPostorder(int*& revEBTPostorder) {
// 扩充结点
if (*revEBTPostorder == -1) {
revEBTPostorder++;
return nullptr;
}
BinaryTreeNode* root = new BinaryTreeNode;
root->m_key = *revEBTPostorder;
revEBTPostorder++;
root->m_pRight = createBTreeEPostorder(revEBTPostorder);
root->m_pLeft = createBTreeEPostorder(revEBTPostorder);
return root;
}
// @brief: 将扩充二叉树后序序列反转后调用建树函数
// @ret: 二叉树根结点
BinaryTreeNode* createBTreeEPostorderWrap(const vector<int>& eBTPostorder) {
int* revEBTPostorder = new int[eBTPostorder.size()];
int* originP = revEBTPostorder;
for (int i = eBTPostorder.size() - 1, j = 0; i >= 0; i--) {
revEBTPostorder[j++] = eBTPostorder[i];
}
auto root = createBTreeEPostorder(revEBTPostorder);
delete[] originP;
return root;
}
验证如下:
int main() {
vector<int> ePreorder = vector<int>{-1, -1, -1, 7, 4, -1, 2, -1, -1, 5, -1, -1, 8, -1, 6, 3, 1};
auto* root = createBTreeEPostorderWrap(kPreorder);
postorderRecursion(root);
}
运行输出:
7 4 2 5 8 6 3 1
7.小结
本文内容还不够完善,只给出了构建方式的递归实现,非递归实现暂未给出,后续会继续完善。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








