Leetcode（46）——全排列

SmileGuy17

已于 2022-07-06 21:23:17 修改

阅读量223

点赞数

分类专栏： Leetcode 文章标签： leetcode 深度优先算法

于 2022-07-06 21:09:39 首次发布

本文链接：https://blog.csdn.net/KCDCY/article/details/125646598

版权

Leetcode 专栏收录该内容

77 篇文章 6 订阅

订阅专栏

Leetcode（46）——全排列

题目

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

$1$ <= nums.length <= $6$
$- 10$ <= nums[i] <= $10$
$n u m s$ 中的所有整数 互不相同

题解

方法一：回溯法

思路

怎样输出所有的排列方式呢？对于每一个当前位置 i，我们可以将其于之后的任意位置交换，然后继续处理位置 i+1，直到处理到最后一位。为了防止每次遍历时都要新建一个子数组储存位置 i 之前已经交换好的数字——我们可以利用回溯法，只对原数组进行修改，在递归完成后再修改回来。

具体来说，假设我们已经填到第 $\textit{first}$ 个位置，那么 $\textit{nums}$ 数组中 $\textit{first} - 1]$ 是已填过的数的集合， $[\textit{first}, n - 1]$ 是待填的数的集合。我们肯定是尝试用 $[\textit{first}, n - 1]$ 里的数去填第 $\textit{first}$ 个数，假设待填的数的下标为 $i$ ，那么填完以后我们将第 $i$ 个数和第 $\textit{first}$ 个数交换，即能使得在填第 $\textit{first} + 1$ 个数的时候 $\textit{nums}$ 数组的 $\textit{first}]$ 部分为已填过的数， $[\textit{first} + 1, n - 1]$ 为待填的数，回溯的时候交换回来即能完成撤销操作。
举个简单的例子，假设我们有 $[2, 5, 8, 9, 10]$ 这 $5$ 个数要填入，已经填到第 $3$ 个位置，已经填了 $[8, 9]$ 两个数，那么这个数组目前为 $[8, 9 ∣ 2, 5, 10]$ 这样的状态，分隔符区分了左右两个部分。假设这个位置我们要填 $10$ 这个数，为了维护数组，我们将 $2$ 和 $10$ 交换，即能使得数组继续保持分隔符左边的数已经填过，右边的待填 $[8, 9, 10 ∣ 2, 5]$ 。

当然我们会发现这样生成的全排列并不是按字典序存储在答案数组中的，如果题目要求按字典序输出，那么请还是用标记数组或者其他方法。

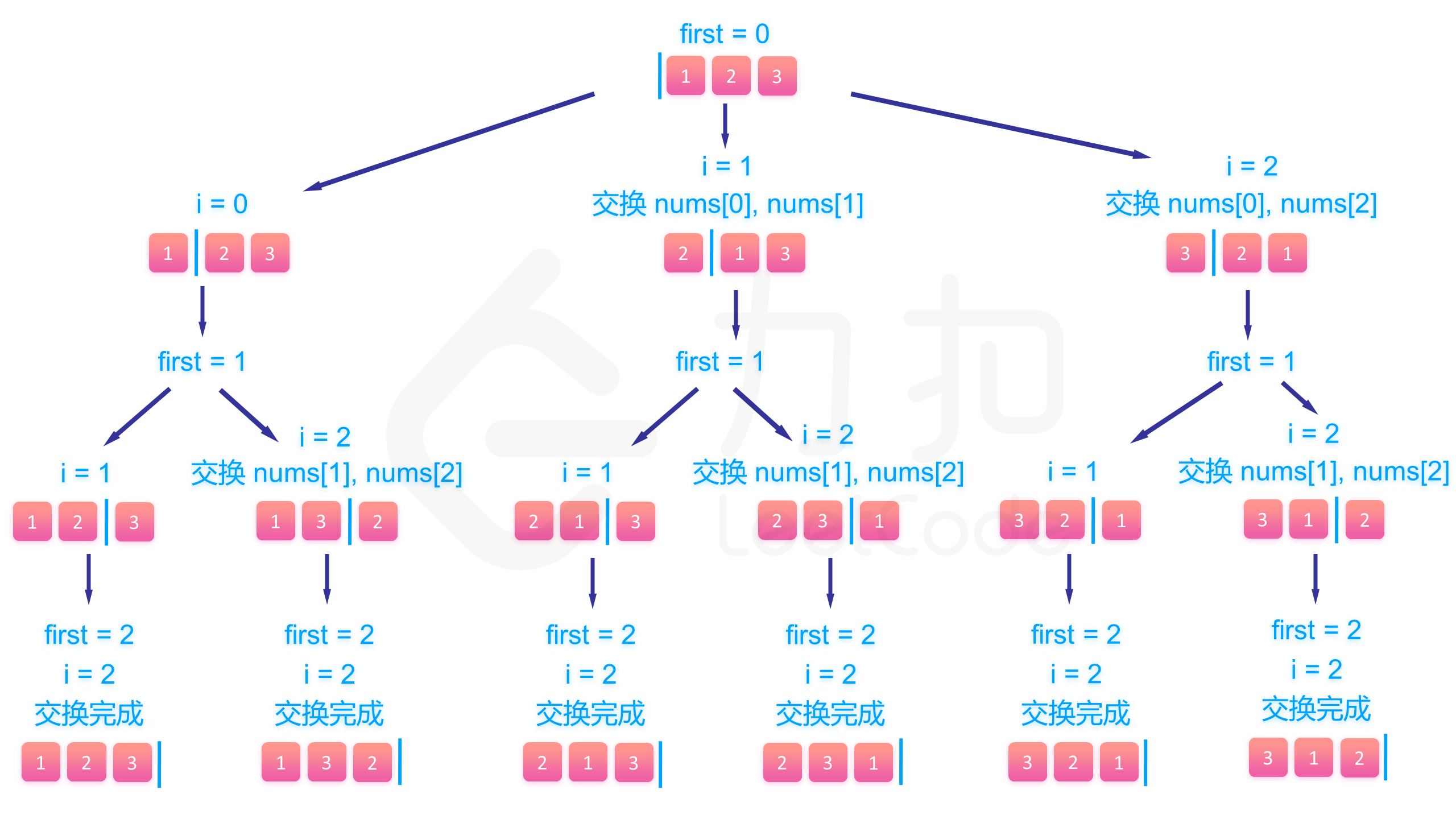
下面的图展示了回溯的整个过程：
在这里插入图片描述

代码实现

Leetcode 官方题解：

class Solution {
public:
    void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
        // 所有数都填完了
        if (first == len) {
            res.emplace_back(output);
            return;
        }
        for (int i = first; i < len; ++i) {
            // 动态维护数组
            swap(output[i], output[first]);
            // 继续递归填下一个数
            backtrack(res, output, first + 1, len);
            // 撤销操作
            swap(output[i], output[first]);
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int> > res;
        backtrack(res, nums, 0, (int)nums.size());
        return res;
    }
};

我自己的：

class Solution {
    void DFS(vector<vector<int>>& ans, vector<int>& s, vector<int>& nums, int p){
        if(s.size() == nums.size()) ans.push_back(s);
        else{
            for(int n = p; n < nums.size(); n++){
                swap(nums[p], nums[n]);
                s.push_back(nums[p]);
                DFS(ans, s, nums, p+1); // 从下标1开始
                s.pop_back();           // 回溯
                swap(nums[p], nums[n]);
            }
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<int> s;
        vector<vector<int>> ans;
        DFS(ans, s, nums, 0);
        return ans;
    }
};

改进后：

class Solution {
    void DFS(vector<vector<int>>& ans, vector<int>& nums, int p){
        if(p+1 == nums.size()) 
            ans.push_back(nums);
        else{
            for(int n = p; n < nums.size(); n++){
                swap(nums[p], nums[n]);
                DFS(ans, nums, p+1);    // 从下标 p+1 开始
                swap(nums[p], nums[n]); // 回溯
            }
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> ans;
        DFS(ans, nums, 0);
        return ans;
    }
};

复杂度分析

时间复杂度： $\times n!)$ ，其中 $n$ 为序列的长度。
算法的复杂度首先受 $\textit{backtrack}$ 的调用次数制约， $\textit{backtrack}$ 的调用次数为 $\sum_{k = 1}^{n}{P(n, k)}$ 次，其中 $\frac{n!}{(n - k)!} = n (n - 1) \ldots (n - k + 1)$ ，该式被称作 n 的 k - 排列，或者部分排列。
而 $\sum_{k = 1}^{n}{P(n, k)} = n! + \frac{n!}{1!} + \frac{n!}{2!} + \frac{n!}{3!} + \ldots + \frac{n!}{(n-1)!} < 2n! + \frac{n!}{2} + \frac{n!}{2^2} + \frac{n!}{2^{n-2}} < 3n!$
这说明 $\textit{backtrack}$ 的调用次数是 $O (n!)$ 的。
而对于 $\textit{backtrack}$ 调用的每个叶结点（共 $n!$ 个），我们需要将当前答案使用 $O (n)$ 的时间复制到答案数组中，相乘得时间复杂度为 $\times n!)$ 。
因此时间复杂度为 $\times n!)$ 。
空间复杂度： $O (n)$ ，其中 $n$ 为序列的长度。除答案数组以外，递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，这里可知递归调用深度为 $O (n)$ 。