【不定期更新篇(未成形篇)】
一直在搞,就像吃很恶习的东西,好想吐;
但还是可以理解成良药苦口啊~;
基础知识定义:
网络是一种特殊的有向图。
有向加权图G,指定两个定点S和T,分别称为源和汇。边上的权值称为容量;
网络中的一个可行流并不是改路线中所有边的容量的简单相加,这段路线的总承重量受路线中最小容量边的制约。
寻找方案使得总运输量最大,这就是网络流算法需要解决的问题;
通俗的讲:(我将说路就是管道,路的权值就是管道的容量)
在一个网络中,往源点灌水,然后从源点水开始流向汇点,
【只考虑在单位时间下】
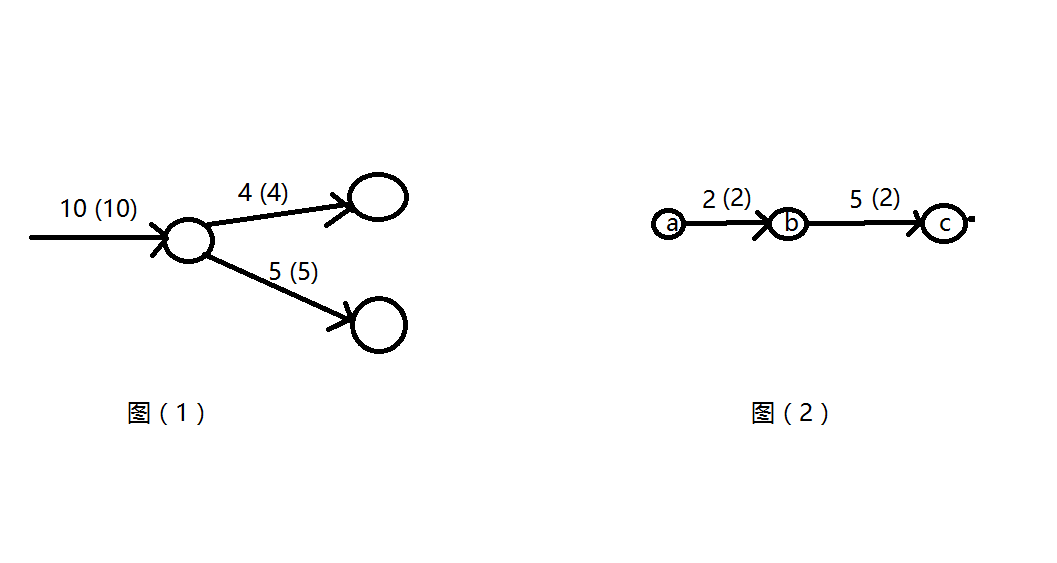
1.如果从大的流分流,分开的流的总和是小于这个流的,那么支流的流量就是本身的容量,见下图(1);
2.如果从小的流往大的容量的管道,那么对于大的管道来说,水流过来才这么点,所以大的管道也才只有之前的那么多水而已啊,见图(2);
一个网络中的最大流就是指该网络中流值最大的流,只是指了某条特定的流,而我们是要通过方法来计算这个最大流的流值是多大。
感觉先搞一下网络流算法EK算法的流程好像还是不懂,真的好无力啊。
可以先打一遍!!!(推荐);
大致流程就是BFS一下,找到一条增广路,搞出一个最小的流值,从源到汇上的路的权值减去这个流值,并且在汇到源上权值加上这个流值;
FF方法的具体步骤(摘自图论书):
(1):初始化网络中所有边的容量,c<u,v>继承该边的容量,c<v,u>初始化为0,其中边<v,u>即为回退边。初始化最大流为0;
(2):在残留网络中找出一条从源S到汇T的增广路p。如果能找到,则转步骤(3);
如不能找到,则转步骤(5).
(3):在增广路p中找出所谓的“瓶颈”边,即路径中容量最小的边,记录下这个值X,并且累加到最大流中,转步骤(4)。
(4):将增广路中所有c< u , v >减去X,所有c<v,u>加上X,构成新的残留网络。转步骤(2).
(5):得到网络的最大流,退出。
const intN=110; //最大点个数
intma[N][N],n,p[N]; //ma:邻接数组;n:点数;p:前驱数组
bool EK_bfs()
{
queue<int>q;//队列
bool flag[N];//标记数组
//初始化
memset(flag,false,sizeof(flag));
memset(p,-1,sizeof(p));
while(!q.empty())
q.pop();
flag[1]=true;
q.push(1);
while(!q.empty())
{
int u=q.front();
q.pop();
if(u==m) //当队列弹出的点为终点时即可判增广路已经找到;
return true;
for(int i=1;i<=m;i++)
{
if(ma[u][i]&&!flag[i])//当边容量非0,且增广点未标记
{
flag[i]=true;
p[i]=u; //记录前驱
q.push(i);
}
}
}
return false;
}
int EK()
{
int u,ans=0,mm;
while(EK_bfs())//当增广成功的时候
{
mm=INF;
u=m;
while(p[u]!=-1)
{
mm=min(mm,ma[p[u]][u]);
u=p[u]; //寻找到“瓶颈”边,并且记录容量(也可以在BFS过程中求出)
}
ans+=mm; //累加进最大流
u=m;
while(p[u]!=-1) //修改路径上边的容量;
{
ma[p[u]][u]-=mm;
ma[u][p[u]]+=mm;
u=p[u];
}
}
return ans;
}
感觉打完了一发。。。还是好难理解是不是,模拟一发吧。。。
原题链接(http://poj.org/problem?id=1273)
给你4个点,5条边;
5 4
1 2 40//代表1到2有40的容量
1 4 20
2 4 20
2 3 30
3 4 10
然后模拟(我就记录个flow的结果,细节上的自行模拟了…)
一开始进去:
初始化,
从源 1 开始,
1->2,flow[2]=40; 2入队;
1->4,flow[4]=20; 4入队;
2->3,flow[3]=min(flow[2],ma[2][3])=20;
2->4,不需要,4已经处理过了
4出队=汇点,返回;
然后回溯一下:找到一个最小的流,然后更新,将找到的增广路把这个残留网络额外的流减去,反向边加上这个值
……
一直循环到找不到增广路为止;
可惜。。。真心好难理解啊。。打完还是似懂非懂,其实最重要的两步就是BFS找增广路,然后构造一下残留网路,一直循环,然后直到找不到增广路,当前的流值,就是最大流;
然后理解Dinic算法,推荐:Comzyh的博客
基本流程:
1.根据残留网络计算层次图;
2.在层次图中使用DFS进行增广直到不存在增广路
3.重复以上步骤直到无法增广
--------补充说明一个找增广的问题;
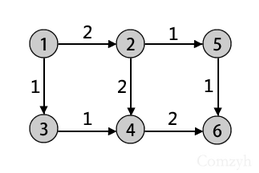
给出这样一副图:
先找到的增广有:
路 流量 转化成 路 流量 路 流量
1->2 2 1<-2 2 1->2 0
2->4 2 4<-2 2 2->4 0
4->6 2 6<-4 2 4->6 0
ok,这样就是找到一个完全的增广;ans+=2;
继续;
1->3 1 3<-1 1 1->3 0
3->4 1 4<-3 1 3->4 0
4->2 2 2->4 1 4->2 1
2->5 1 5->2 1 2->5 0
5->6 1 6->5 1 5->6 0
ok,又是一个增广 ;ans+=1;
终点阐述反向弧的作用:
反向弧可以理解我给这条路分配了x的流量,我建立一个反向弧,等下给自己一个后悔的机会。
比如上面那个第一次找增广过程中4->2建立反向弧,在第二次找增广的时候利用了这个反向弧;
我们可以理解之前我先安排2单位水通过这条路,不要理解成是这条路给的流量,流量都是从源点出发的,很自然这条路上的流量是上面那条路的流量流过来。
对于第一次,留多少呢,我先流个2吧,然后给自己一个机会(建立一个反向弧),等会可能我往这个方向不流2,比如第二次找到了,我可以去别的方向流1,那多个机会流还不好啊,形象上的理解就是上面那个点出来的分流了;
那么还有一个问题,怎么理解反向弧前面的那些路呢?
是不是可以理解这条路(3->4)的流能到达路(2->4)到达4这个点,然而4以后已经阻断了,或者说已经塞了一部分流量了,
然后呢可以利用路(2->4)的反向弧(4->2),索取一部分他的,后悔以后就是说前面那个点(2)在这里分流了,注意每次找的增广都是一个能实现的图上的一个"瓶颈",
然后点(2)分流,实际上是给路(2->5)1单位,给路(2->4)1单位,然后路(3->4)往点4运了1单位,4->6流向6就是2单位;
贴一发DINIC的模板;
邻接矩阵版本:
const int INF=0x3f3f3f3f;
const int N=1e3+10;
int ma[N][N];
int dis[N];
int q[N*100],h,r;
int n,m,ans;
bool BFS()
{
int i,j;
memset(dis,-1,sizeof(dis));
dis[1]=0;
h=0,r=1;
q[1]=1;
while(h<r)
{
j=q[++h];
for(i=1;i<=n;i++)
{
if(dis[i]<0&&ma[j][i]>0)
{
dis[i]=dis[j]+1;
q[++r]=i;
}
}
}
if(dis[n]>0)
return true;
return false;
}
int DFS(int x,int low)
{
int i,a=0;
if(x==n)
return low;
for(int i=1;i<=n;i++)
{
if(ma[x][i]>0&&dis[i]==dis[x]+1&&(a=DFS(i,min(low,ma[x][i]))))
{
ma[x][i]-=a;
ma[i][x]+=a;
return a;
}
}
return 0;
}
void DINIC()
{
int tans;
ans=0;
while(BFS())
{
while(tans=DFS(1,INF))
ans+=tans;
}
printf("%d\n",ans);
}前向星版本:HDU(3549)
#include<bits/stdc++.h>
using namespace std;
typedef __int64 LL;
const int INF=0x3f3f3f3f;
const int N=2050;
int level[N];
int q[N],h;
int n,m,ans;
struct asd{
int to;
int w;
int next;
};
asd edge[2500000];
int head[2500000],tol;
bool BFS(int s,int t)
{
int i,k;
int top;
memset(level,0,sizeof(level));
level[s]=1;
h=0;
q[h++]=s;
for(int i=0;i<h;i++)
{
top=q[i];
if(top==t)
return true;
for(k=head[top];k!=-1;k=edge[k].next)
{
if(!level[edge[k].to]&&edge[k].w>0)
{
q[h++]=edge[k].to;
level[edge[k].to]=level[top]+1;
}
}
}
return false;
}
int DFS(int now,int maxw,int t)
{
int w,k,ret=0;
if(now==t)
return maxw;
for(k=head[now];k!=-1;k=edge[k].next)
{
if(edge[k].w>0&&level[edge[k].to]==level[now]+1)
{
w=DFS(edge[k].to,min(maxw-ret,edge[k].w),t);
edge[k].w-=w;
edge[k^1].w+=w;
ret+=w;
if(ret==maxw)
return ret;
}
}
return ret;
}
void DINIC()
{
ans=0;
while(BFS(1,n))
ans+=DFS(1,INF,n);
printf("%d\n",ans);
}
void add(int a,int b,int c)
{
edge[tol].w=c;
edge[tol].to=b;
edge[tol].next=head[a];
head[a]=tol++;
}
int main()
{
int T,cas=1;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
int u,v,x;
tol=0;
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&x);
add(u,v,x);
add(v,u,0);
}
printf("Case %d: ",cas++);
DINIC();
}
return 0;
}SAP 最大流 双向图模板
//#include <bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<map>
#include<queue>
#include<cmath>
#include<algorithm>
typedef long long LL;
using namespace std;
//#pragma comment(linker, "/STACK:102400000,102400000")
/*
给出起点,终点,边数。
然后双向边(u,v,w)
求最大流;
*/
const int INF = 0x3f3f3f3f;
const int MAXN = 110;//点数的最大值
const int MAXM = 100010;//边数的最大值
struct Edge
{
int to, next, cap, flow;
}edge[MAXM];//注意是MAXM
int tol;
int head[MAXN];
int gap[MAXN], dep[MAXN], pre[MAXN], cur[MAXN];
void init()
{
tol = 0;
memset(head, -1, sizeof(head));
}
//加边,单向图三个参数,双向图四个参数
void addedge(int u, int v, int w, int rw = 0)
{
edge[tol].to = v; edge[tol].cap = w; edge[tol].next = head[u];
edge[tol].flow = 0; head[u] = tol++;
edge[tol].to = u; edge[tol].cap = rw; edge[tol].next = head[v];
edge[tol].flow = 0; head[v] = tol++;
}
//输入参数:起点、终点、点的总数
//点的编号没有影响,只要输入点的总数
int sap(int start, int end, int N)
{
memset(gap, 0, sizeof(gap));
memset(dep, 0, sizeof(dep));
memcpy(cur, head, sizeof(head));
int u = start;
pre[u] = -1;
gap[0] = N;
int ans = 0;
while (dep[start] < N)
{
if (u == end)
{
int Min = INF;
for (int i = pre[u]; i != -1; i = pre[edge[i ^ 1].to])
if (Min > edge[i].cap - edge[i].flow)
Min = edge[i].cap - edge[i].flow;
for (int i = pre[u]; i != -1; i = pre[edge[i ^ 1].to])
{
edge[i].flow += Min;
edge[i ^ 1].flow -= Min;
}
u = start;
ans += Min;
continue;
}
bool flag = false;
int v;
for (int i = cur[u]; i != -1; i = edge[i].next)
{
v = edge[i].to;
if (edge[i].cap - edge[i].flow && dep[v] + 1 == dep[u])
{
flag = true;
cur[u] = pre[v] = i;
break;
}
}
if (flag)
{
u = v;
continue;
}
int Min = N;
for (int i = head[u]; i != -1; i = edge[i].next)
if (edge[i].cap - edge[i].flow && dep[edge[i].to] < Min)
{
Min = dep[edge[i].to];
cur[u] = i;
}
gap[dep[u]]--;
if (!gap[dep[u]])return ans;
dep[u] = Min + 1;
gap[dep[u]]++;
if (u != start) u = edge[pre[u] ^ 1].to;
}
return ans;
}
int m, n, s, t;
int a, b, c;
int main()
{
int T, cases = 1;
scanf("%d", &T);
while (T--)
{
init();
scanf("%d", &n);
scanf("%d%d%d", &s, &t, &m);
while (m--)
{
scanf("%d%d%d", &a, &b, &c);
if (a != b)
{
addedge(a, b, c, c);
}
}
int ans = sap(s, t, n);
printf("Case %d: %d\n", cases++, ans);
}
return 0;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








