AVL树-JAVA-图示/代码
图片转自:http://blog.csdn.net/collonn/article/details/20128205
ADT:
public interface AVLTree {
boolean insert(Node node, int value);
boolean delete(int value);
Node find(int value);
boolean isBalanced(Node node);
boolean singleRotateToLeft(Node node);
boolean singleRotateToRight(Node node);
boolean doubleRotateToLR(Node node);
boolean doubleRotateToRL(Node node);
int height(Node node);
void LDR(Node node);
}
实现代码:
public class AVLTreeImpl implements AVLTree {
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
@Override
public boolean insert(Node node, int value) {
// TODO Auto-generated method stub
//如果root为null,将值赋给root后结束
if (root == null) {
root = new Node(value, null, null);
return true;
}
//如果node参数为null的话,将根root赋给node后继续
if (node == null) {
node = root;
}
if (value < node.getValue()) {
if (node.getLeft() == null) {
node.setLeft(new Node(value, null, null));
} else {
insert(node.getLeft(), value);
}
//插入后发现树不平衡,平衡一下
if (!isBalanced(node)) {
if (value < node.getLeft().getValue()) {
singleRotateToRight(node);
} else {
doubleRotateToLR(node);
}
}
} else {
if (node.getRight() == null) {
node.setRight(new Node(value, null, null));
} else {
insert(node.getRight(), value);
}
//插入后发现树不平衡,平衡一下
if (!isBalanced(node)) {
if (value < node.getLeft().getValue()) {
doubleRotateToRL(node);
} else {
singleRotateToLeft(node);
}
}
}
return true;
}
@Override
public boolean delete(int value) {
// TODO Auto-generated method stub
return false;
}
@Override
public Node find(int value) {
// TODO Auto-generated method stub
return null;
}
//单步向右转
@Override
public boolean singleRotateToLeft(Node node) {
// TODO Auto-generated method stub
if (node == null || node.getRight() == null)
return false;
Node recordRoot = node;
Node recordRight = node.getRight();
if (recordRight.getLeft() != null) {
recordRoot.setRight(recordRight.getLeft());
}
recordRight.setLeft(recordRoot);
return true;
}
//单步向左转
@Override
public boolean singleRotateToRight(Node node) {
// TODO Auto-generated method stub
if (node == null || node.getLeft() == null)
return false;
Node recordRoot = node;
Node recordLeft = node.getLeft();
if (recordLeft.getRight() != null) {
recordRoot.setLeft(recordLeft.getRight());
}
recordLeft.setRight(recordRoot);
return true;
}
//双步旋转先左后右
@Override
public boolean doubleRotateToLR(Node node) {
// TODO Auto-generated method stub
if (!singleRotateToLeft(node.getLeft())) {
return false;
}
if (!singleRotateToRight(node)) {
return false;
}
return true;
}
//双步旋转先右后左
@Override
public boolean doubleRotateToRL(Node node) {
// TODO Auto-generated method stub
if (!singleRotateToRight(node.getRight())) {
return false;
}
if (!singleRotateToLeft(node)) {
return false;
}
return true;
}
//求节点的高度
@Override
public int height(Node node) {
// TODO Auto-generated method stub
if (node == null)
return 0;
int heightL = height(node.getLeft());
int heightR = height(node.getRight());
return heightL <= heightR ? heightR : heightL;
}
//中序遍历
@Override
public void LDR(Node node) {
// TODO Auto-generated method stub
if(node == null) return;
LDR(node.getLeft());
System.out.println("value:" + node.getValue() + ", left:" + node.getLeft() + ", right:" + node.getRight());
LDR(node.getRight());
}
//平衡判断
@Override
public boolean isBalanced(Node node) {
// TODO Auto-generated method stub
if (Math.abs(height(node.getLeft()) - height(node.getRight())) > 1) {
return false;
}
return true;
}
@Override
public String toString() {
// TODO Auto-generated method stub
return root.toString();
}
}
测试代码:
public static void main(String[] args) {
AVLTreeImpl avl = new AVLTreeImpl();
avl.insert(null, 5);
avl.insert(null, 4);
avl.insert(null, 3);
avl.insert(null, 2);
avl.insert(null, 1);
avl.insert(null, 8);
avl.LDR(avl.getRoot()); //中序遍历
}
结果:
value:1, left:null, right:null
value:2, left:1, right:null
value:3, left:2, right:null
value:4, left:3, right:null
value:5, left:4, right:8
value:8, left:null, right:null
delete
你可能注意到上面没有写delete方法,因为delete方法与比insert方法还要复杂。
删除节点的处理:
删除节点的三种情况:
1)删除节点无左节点,也无右节点:
直接删除,之后向上递归平衡。
2)删除节点只有一个节点:
直接删除后接上子节点,之后向上递归平衡。
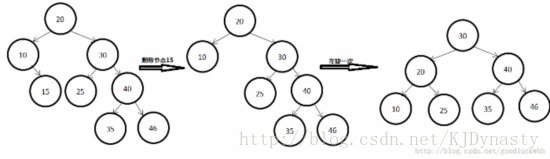
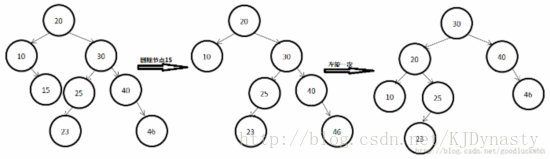
3)删除节点有两个节点:
将左子树最大值与删除节点交换。删除交换后的节点,之后向上递归平衡。
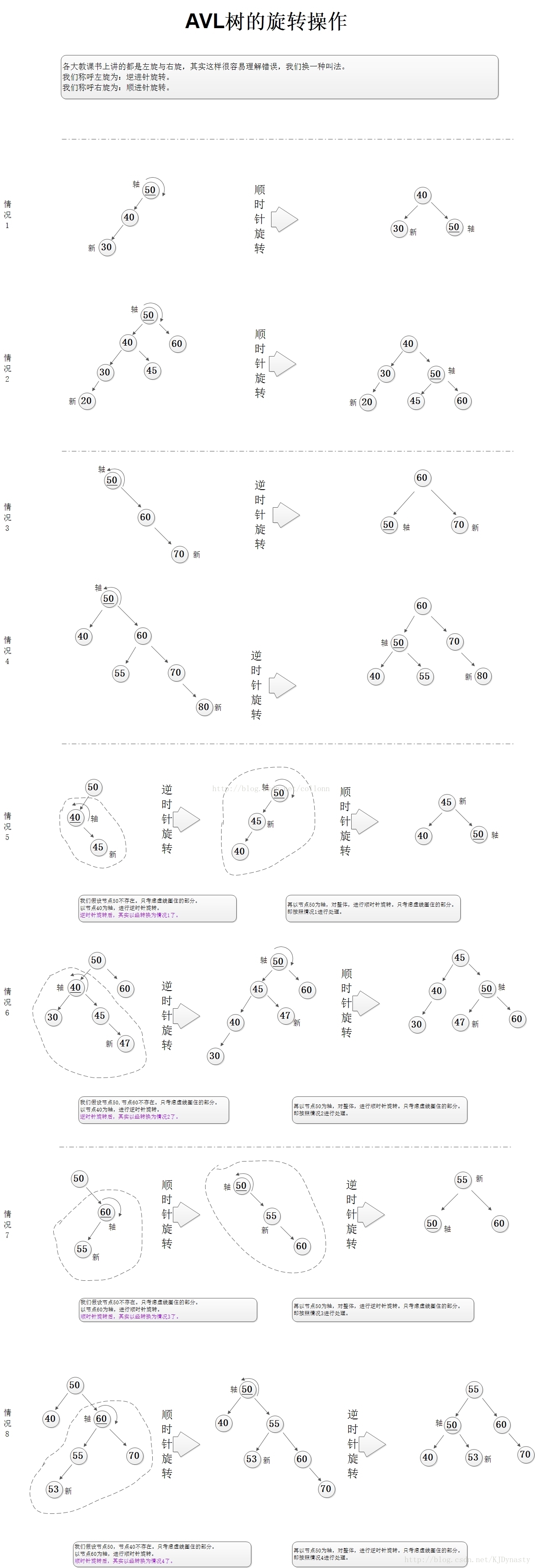
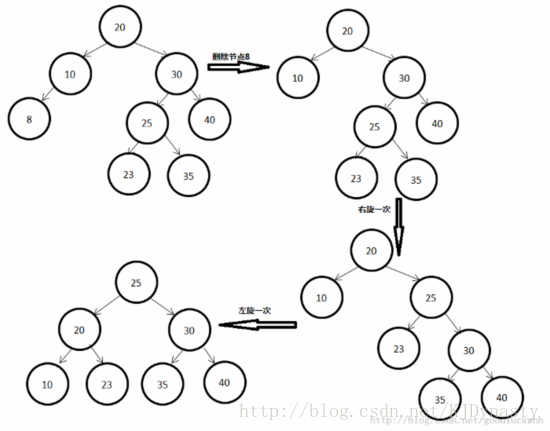
失衡情况下的平衡处理:
1)失衡结点 的右子树的平衡因子为-1
2)失衡结点的右子树的平衡因子为0
3)失衡结点的右子树的平衡因子为1
delete代码
代码太多,写乱了。








 本文介绍了一种自平衡二叉搜索树——AVL树的Java实现。包括AVL树的基本操作如插入、查找等,并提供了详细的代码实现及图示说明。还介绍了如何通过旋转保持树的平衡。
本文介绍了一种自平衡二叉搜索树——AVL树的Java实现。包括AVL树的基本操作如插入、查找等,并提供了详细的代码实现及图示说明。还介绍了如何通过旋转保持树的平衡。
















 1216
1216

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








