一致性哈希及java实现

最新推荐文章于 2022-09-05 17:55:03 发布
最新推荐文章于 2022-09-05 17:55:03 发布
阅读量2.1k 收藏 6
点赞数
分类专栏： 算法题 java 文章标签： hash 一致性hash 实现 原理

1、一致性hash介绍

一致性哈希算法是分布式系统中常用的算法。比如，一个分布式的存储系统，要将数据存储到具体的节点上，如果采用普通的hash方法，将数据映射到具体的节点上，如key%N，key是数据的key，N是机器节点数，如果有一个机器加入或退出这个集群，则所有的数据映射都无效了，如果是持久化存储则要做数据迁移，如果是分布式缓存，则其他缓存就失效了。

    因此，引入了一致性哈希算法：


 

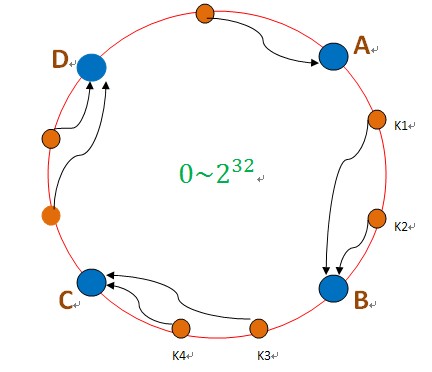
把数据用hash函数（如MD5），映射到一个很大的空间里，如图所示。数据的存储时，先得到一个hash值，对应到这个环中的每个位置，如k1对应到了图中所示的位置，然后沿顺时针找到一个机器节点B，将k1存储到B这个节点中。

如果B节点宕机了，则B上的数据就会落到C节点上，如下图所示：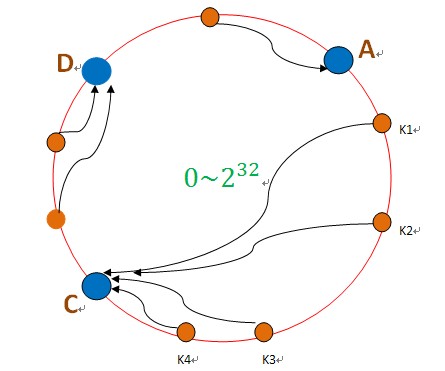


 

这样，只会影响C节点，对其他的节点A，D的数据不会造成影响。然而，这又会造成一个“雪崩”的情况，即C节点由于承担了B节点的数据，所以C节点的负载会变高，C节点很容易也宕机，这样依次下去，这样造成整个集群都挂了。

       为此，引入了“虚拟节点”的概念：即把想象在这个环上有很多“虚拟节点”，数据的存储是沿着环的顺时针方向找一个虚拟节点，每个虚拟节点都会关联到一个真实节点，如下图所使用：


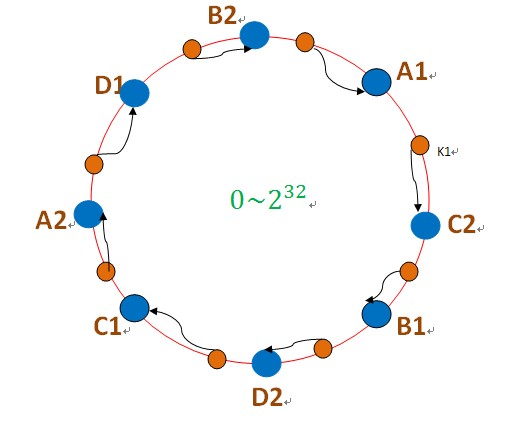
图中的A1、A2、B1、B2、C1、C2、D1、D2都是虚拟节点，机器A负载存储A1、A2的数据，机器B负载存储B1、B2的数据，机器C负载存储C1、C2的数据。由于这些虚拟节点数量很多，均匀分布，因此不会造成“雪崩”现象。

2、实现原理

web架构中，分布式是个常见的架构设计。尤其是大家比较熟悉的Memcached，或者其他cache产品常常被设计成分布式集群。分布式往往采用hash(key)%n 的方式，但这种算法比较简单，便于实现和理解。但弊端是不能动态增删节点。比较合理的方法改用一致性哈希(consistent hashing)分布。一致性哈希，简单的说在移除 / 添加一个 cache 时，它能够尽可能小的改变已存在 key 映射关系，尽可能的满足单调性的要求。原理不再赘述，google和度娘都能得到答案。重点说一下最常见的实现方式。

 

Java中采用md5散列的方式，计算hash值，这样基本上能保证key散列出啦的hash不会重复。

Java代码   收藏代码
  1. private static long md5HashingAlg(String key) {  
  2.     MessageDigest md5 = MD5.get();  
  3.     md5.reset();  
  4.     md5.update(key.getBytes());  
  5.     byte[] bKey = md5.digest();  
  6.     long res = ((long) (bKey[3] & 0xFF) << 24) | ((long) (bKey[2] & 0xFF) << 16) | ((long) (bKey[1] & 0xFF) << 8)| (long) (bKey[0] & 0xFF);  
  7.     return res;  
  8. }  

在对server节点初始化的时候，为了避免节点过少数据分布不均匀，都会初始化一些虚拟节点。具体方法上面计算hash值的方式类同，一把采用根据权重虚拟出来一些key，具体不过多介绍。

一致性哈希算法中，把哈希值想象成一个环状。有关一致性哈希算法，介绍里面说0~2^32-1的数据，不要误以为哈希环要保存2^32个数据。他只是说，哈希环存的key的哈希值范围是0~2^32-1，并不是key的哈希值要覆盖0~2^32-1所有数据。


既要保存hash值，又要保存对应的节点地址，貌似最简单的就是map，在Java中没有什么map可以满足是个环状。那就找一个排序的，0开头，2^32-1做尾。查找时查到尾没有结果，再返回头找这样可以理解为是个环状了。

在初始化的时候，把节点的hash和节点地址保存在TreeMap里，client查找时，根据key的hash值去treeMap得到自己应该查询的节点，往下查找比自己hash值大的，如果有则得到结果返回。如果没有，则回到treeMap的头，取第一个返回结果。

如图中所示：根据key计算出hash，去treeMap查找比key哈希大的那部分，取出第一个值就是结果。如果没有别key哈希大的部分，则取treeMap的第一个值。


代码的实现：

Java代码   收藏代码
  1. private final Long findPointFor(Long hv) {  
  2.   
  3.         SortedMap<Long, String> tmap = this.consistentBuckets.tailMap(hv);  
  4.   
  5.         return (tmap.isEmpty()) ? this.consistentBuckets.firstKey() : tmap.firstKey();  
  6. }  


3、代码实现

这几天看了几遍一致性哈希的文章，但是都没有比较完整的实现，因此试着实现了一下，这里我就不讲一致性哈希的原理了，网上很多，以一致性哈希用在负载均衡的实例来说，一致性哈希就是先把主机ip从小大到全部放到一个环内，然后客户端ip来连接的时候，把客户端ip连接到大小最接近客户端ip且大于客户端ip的主机。当然，这里的ip一般都是要先hash一下的。我的程序运行结果如下：

    

[java]  view plain copy print ?
  1. 添加客户端，一开始有4个主机，分别为s1,s2,s3,s4,每个主机有100个虚拟主机：  
  2. 101客户端（hash：-3872430075274208315）连接到主机->s2-192.168.1.2  
  3. 102客户端（hash：-6461488502093916753）连接到主机->s1-192.168.1.1  
  4. 103客户端（hash：-3272337528088901176）连接到主机->s3-192.168.1.3  
  5. 104客户端（hash：7274050343425899995）连接到主机->s2-192.168.1.2  
  6. 105客户端（hash：6218187750346216421）连接到主机->s1-192.168.1.1  
  7. 106客户端（hash：-8497989778066313989）连接到主机->s2-192.168.1.2  
  8. 107客户端（hash：2219601794372203979）连接到主机->s3-192.168.1.3  
  9. 108客户端（hash：1903054837754071260）连接到主机->s3-192.168.1.3  
  10. 109客户端（hash：-2425484502654523425）连接到主机->s1-192.168.1.1  
  11. 删除主机s2-192.168.1.2的变化：  
  12. hash(-8497989778066313989)改变到->s4-192.168.1.4  
  13. hash(7274050343425899995)改变到->s2-192.168.1.2  
  14. hash(-3872430075274208315)改变到->s4-192.168.1.4  
  15. hash(7274050343425899995)改变到->s1-192.168.1.1  
  16. 增加主机s5-192.168.1.5的变化：  
  17. hash(1903054837754071260)改变到->s5-192.168.1.5  
  18. hash(1903054837754071260)改变到->s5-192.168.1.5  
  19. hash(-3272337528088901176)改变到->s5-192.168.1.5  
  20. 最后的客户端到主机的映射为：  
  21. hash(-8497989778066313989)连接到主机->s4-192.168.1.4  
  22. hash(-6461488502093916753)连接到主机->s1-192.168.1.1  
  23. hash(-3872430075274208315)连接到主机->s4-192.168.1.4  
  24. hash(-3272337528088901176)连接到主机->s5-192.168.1.5  
  25. hash(-2425484502654523425)连接到主机->s1-192.168.1.1  
  26. hash(1903054837754071260)连接到主机->s5-192.168.1.5  
  27. hash(2219601794372203979)连接到主机->s3-192.168.1.3  
  28. hash(6218187750346216421)连接到主机->s1-192.168.1.1  
  29. hash(7274050343425899995)连接到主机->s1-192.168.1.1  

看结果可知：一开始添加到9个客户端，连接到主机s1，s2，s3，s4的客户端分别有3，3，3，0个，经过删除主机s2，添加主机s5，最后9个客户端分别连接到主机s1,s2,s3,s4,s5的个数为4，0，１，２，２.这里要说明一下删除主机s2的情况，hash尾号为9995的客户端先连接到s2，再连接到s1，为什么会出现这种情况呢？因为每一个真实主机有ｎ个虚拟主机，删除ｓ２却打印“hash(7274050343425899995)改变到->s2-192.168.1.2”是因为删除了ｓ２的其中一个虚拟主机，跳转到另一个虚拟主机，但还是在ｓ２上，当然，这里是打印中间情况，以便了解，真实的环境是删除了ｓ２后，所有他的虚拟节点都会马上被删除，虚拟节点上的连接也会重新连接到另一个主机的虚拟节点，不会存在这种中间情况。

以下给出所有的实现代码，大家共同学习：

[java]  view plain copy print ?
  1. public class Shard<Node> { // S类封装了机器节点的信息 ，如name、password、ip、port等  
  2.   
  3.     static private TreeMap<Long, Node> nodes; // 虚拟节点到真实节点的映射  
  4.     static private TreeMap<Long,Node> treeKey; //key到真实节点的映射  
  5.     static private List<Node> shards = new ArrayList<Node>(); // 真实机器节点  
  6.     private final int NODE_NUM = 100; // 每个机器节点关联的虚拟节点个数  
  7.     boolean flag = false;  
  8.       
  9.     public Shard(List<Node> shards) {  
  10.         super();  
  11.         this.shards = shards;  
  12.         init();  
  13.     }  
  14.   
  15.     public static void main(String[] args) {  
  16. //      System.out.println(hash("w222o1d"));  
  17. //      System.out.println(Long.MIN_VALUE);  
  18. //      System.out.println(Long.MAX_VALUE);  
  19.         Node s1 = new Node("s1", "192.168.1.1");  
  20.         Node s2 = new Node("s2", "192.168.1.2");  
  21.         Node s3 = new Node("s3", "192.168.1.3");  
  22.         Node s4 = new Node("s4", "192.168.1.4");  
  23.         Node s5 = new Node("s5","192.168.1.5");  
  24.         shards.add(s1);  
  25.         shards.add(s2);  
  26.         shards.add(s3);  
  27.         shards.add(s4);  
  28.         Shard<Node> sh = new Shard<Shard.Node>(shards);  
  29.         System.out.println("添加客户端，一开始有4个主机，分别为s1,s2,s3,s4,每个主机有100个虚拟主机：");  
  30.         sh.keyToNode("101客户端");  
  31.         sh.keyToNode("102客户端");  
  32.         sh.keyToNode("103客户端");  
  33.         sh.keyToNode("104客户端");  
  34.         sh.keyToNode("105客户端");  
  35.         sh.keyToNode("106客户端");  
  36.         sh.keyToNode("107客户端");  
  37.         sh.keyToNode("108客户端");  
  38.         sh.keyToNode("109客户端");  
  39.           
  40.         sh.deleteS(s2);  
  41.           
  42.           
  43.         sh.addS(s5);  
  44.           
  45.         System.out.println("最后的客户端到主机的映射为：");  
  46.         printKeyTree();  
  47.     }  
  48.     public static void printKeyTree(){  
  49.         for(Iterator<Long> it = treeKey.keySet().iterator();it.hasNext();){  
  50.             Long lo = it.next();  
  51.             System.out.println("hash("+lo+")连接到主机->"+treeKey.get(lo));  
  52.         }  
  53.           
  54.     }  
  55.       
  56.     private void init() { // 初始化一致性hash环  
  57.         nodes = new TreeMap<Long, Node>();  
  58.         treeKey = new TreeMap<Long, Node>();  
  59.         for (int i = 0; i != shards.size(); ++i) { // 每个真实机器节点都需要关联虚拟节点  
  60.             final Node shardInfo = shards.get(i);  
  61.   
  62.             for (int n = 0; n < NODE_NUM; n++)  
  63.                 // 一个真实机器节点关联NODE_NUM个虚拟节点  
  64.                 nodes.put(hash("SHARD-" + shardInfo.name + "-NODE-" + n), shardInfo);  
  65.         }  
  66.     }  
  67.     //增加一个主机  
  68.     private void addS(Node s) {  
  69.         System.out.println("增加主机"+s+"的变化：");  
  70.         for (int n = 0; n < NODE_NUM; n++)  
  71.             addS(hash("SHARD-" + s.name + "-NODE-" + n), s);  
  72.   
  73.     }  
  74.       
  75.     //添加一个虚拟节点进环形结构,lg为虚拟节点的hash值  
  76.     public void addS(Long lg,Node s){  
  77.         SortedMap<Long, Node> tail = nodes.tailMap(lg);  
  78.         SortedMap<Long,Node>  head = nodes.headMap(lg);  
  79.         Long begin = 0L;  
  80.         Long end = 0L;  
  81.         SortedMap<Long, Node> between;  
  82.         if(head.size()==0){  
  83.             between = treeKey.tailMap(nodes.lastKey());  
  84.             flag = true;  
  85.         }else{  
  86.             begin = head.lastKey();  
  87.             between = treeKey.subMap(begin, lg);  
  88.             flag = false;  
  89.         }  
  90.         nodes.put(lg, s);  
  91.         for(Iterator<Long> it=between.keySet().iterator();it.hasNext();){  
  92.             Long lo = it.next();  
  93.             if(flag){  
  94.                 treeKey.put(lo, nodes.get(lg));  
  95.                 System.out.println("hash("+lo+")改变到->"+tail.get(tail.firstKey()));  
  96.             }else{  
  97.                 treeKey.put(lo, nodes.get(lg));  
  98.                 System.out.println("hash("+lo+")改变到->"+tail.get(tail.firstKey()));  
  99.             }  
  100.         }  
  101.     }  
  102.       
  103.     //删除真实节点是s  
  104.     public void deleteS(Node s){  
  105.         if(s==null){  
  106.             return;  
  107.         }  
  108.         System.out.println("删除主机"+s+"的变化：");      
  109.         for(int i=0;i<NODE_NUM;i++){  
  110.             //定位s节点的第i的虚拟节点的位置  
  111.             SortedMap<Long, Node> tail = nodes.tailMap(hash("SHARD-" + s.name + "-NODE-" + i));  
  112.             SortedMap<Long,Node>  head = nodes.headMap(hash("SHARD-" + s.name + "-NODE-" + i));  
  113.             Long begin = 0L;  
  114.             Long end = 0L;  
  115.               
  116.             SortedMap<Long, Node> between;  
  117.             if(head.size()==0){  
  118.                 between = treeKey.tailMap(nodes.lastKey());  
  119.                 end = tail.firstKey();  
  120.                 tail.remove(tail.firstKey());  
  121.                 nodes.remove(tail.firstKey());//从nodes中删除s节点的第i个虚拟节点  
  122.                 flag = true;  
  123.             }else{  
  124.                 begin = head.lastKey();  
  125.                 end = tail.firstKey();  
  126.                 tail.remove(tail.firstKey());  
  127.                 between = treeKey.subMap(begin, end);//在s节点的第i个虚拟节点的所有key的集合  
  128.                 flag = false;  
  129.             }  
  130.             for(Iterator<Long> it = between.keySet().iterator();it.hasNext();){  
  131.                 Long lo  = it.next();  
  132.                 if(flag){  
  133.                     treeKey.put(lo, tail.get(tail.firstKey()));  
  134.                     System.out.println("hash("+lo+")改变到->"+tail.get(tail.firstKey()));  
  135.                 }else{  
  136.                     treeKey.put(lo, tail.get(tail.firstKey()));  
  137.                     System.out.println("hash("+lo+")改变到->"+tail.get(tail.firstKey()));  
  138.                 }  
  139.             }  
  140.         }  
  141.           
  142.     }  
  143.   
  144.     //映射key到真实节点  
  145.     public void keyToNode(String key){  
  146.         SortedMap<Long, Node> tail = nodes.tailMap(hash(key)); // 沿环的顺时针找到一个虚拟节点  
  147.         if (tail.size() == 0) {  
  148.             return;  
  149.         }  
  150.         treeKey.put(hash(key), tail.get(tail.firstKey()));  
  151.         System.out.println(key+"（hash："+hash(key)+"）连接到主机->"+tail.get(tail.firstKey()));  
  152.     }  
  153.       
  154.     /** 
  155.      *  MurMurHash算法，是非加密HASH算法，性能很高， 
  156.      *  比传统的CRC32,MD5，SHA-1（这两个算法都是加密HASH算法，复杂度本身就很高，带来的性能上的损害也不可避免） 
  157.      *  等HASH算法要快很多，而且据说这个算法的碰撞率很低. 
  158.      *  http://murmurhash.googlepages.com/ 
  159.      */  
  160.     private static Long hash(String key) {  
  161.           
  162.         ByteBuffer buf = ByteBuffer.wrap(key.getBytes());  
  163.         int seed = 0x1234ABCD;  
  164.           
  165.         ByteOrder byteOrder = buf.order();  
  166.         buf.order(ByteOrder.LITTLE_ENDIAN);  
  167.   
  168.         long m = 0xc6a4a7935bd1e995L;  
  169.         int r = 47;  
  170.   
  171.         long h = seed ^ (buf.remaining() * m);  
  172.   
  173.         long k;  
  174.         while (buf.remaining() >= 8) {  
  175.             k = buf.getLong();  
  176.   
  177.             k *= m;  
  178.             k ^= k >>> r;  
  179.             k *= m;  
  180.   
  181.             h ^= k;  
  182.             h *= m;  
  183.         }  
  184.   
  185.         if (buf.remaining() > 0) {  
  186.             ByteBuffer finish = ByteBuffer.allocate(8).order(  
  187.                     ByteOrder.LITTLE_ENDIAN);  
  188.             // for big-endian version, do this first:  
  189.             // finish.position(8-buf.remaining());  
  190.             finish.put(buf).rewind();  
  191.             h ^= finish.getLong();  
  192.             h *= m;  
  193.         }  
  194.   
  195.         h ^= h >>> r;  
  196.         h *= m;  
  197.         h ^= h >>> r;  
  198.   
  199.         buf.order(byteOrder);  
  200.         return h;  
  201.     }  
  202.       
  203.     static class Node{  
  204.         String name;  
  205.         String ip;  
  206.         public Node(String name,String ip) {  
  207.             this.name = name;  
  208.             this.ip = ip;  
  209.         }  
  210.         @Override  
  211.         public String toString() {  
  212.             return this.name+"-"+this.ip;  
  213.         }  
  214.     }  
  215.   
  216. }

4、关于treeMap的一些方法的介绍

4.1 tailMap（）

tailMap(K fromKey) 方法用于返回此映射，其键大于或等于fromKey的部分视图。返回的映射受此映射支持，因此改变返回映射反映在此映射中，反之亦然。

以下是java.util.TreeMap.tailMap()方法的声明。

public SortedMap<K,V> tailMap(K fromKey)
参数
fromKey--返回映射中键的低端点(包括)

返回值

该方法调用返回此映射，其键大于或等于fromKey的部分视图。

例子：

下面的示例演示java.util.TreeMap.tailMap()方法的使用

package com.yiibai;

import java.util.*;

public class TreeMapDemo {
   public static void main(String[] args) {
      // creating maps 
      TreeMap<Integer, String> treemap = new TreeMap<Integer, String>();
      SortedMap<Integer, String> treemapincl = new TreeMap<Integer, String>();
            
      // populating tree map
      treemap.put(2, "two");
      treemap.put(1, "one");
      treemap.put(3, "three");
      treemap.put(6, "six");
      treemap.put(5, "five");      
      
      System.out.println("Getting tail map");
      treemapincl=treemap.tailMap(3);
      System.out.println("Tail map values: "+treemapincl);      
   }    
}

现在编译和运行上面的代码示例，将产生以下结果。

Getting tail map
Tail map values: {3=three, 5=five, 6=six}

4.2 headMap（）

headMap(K toKey)  方法用于返回此映射的键严格小于toKey的部分视图。

4.3 java.util.TreeMap类

java.util.TreeMap 类是Red-Black树实现基于Map接口。以下是关于TreeMap中重要的几点：

TreeMap类保证该映射将是升序键顺序。

该映射是按照自然排序方法的关键类，或者根据创建映射时提供的比较器，这将取决于其构造函数中使用排序。

kaiseu
关注
专栏目录
一致性Hash算法Java版实现
Silently9527’s Blog
01-12 361
本文已被Github仓库收录 https://github.com/silently9527/JavaCore 微信公众号：贝塔学Java 前言 在之前写了两篇关于缓存的文章《万字长文聊缓存（上）- http缓存》《万字长文聊缓存（下）- 应用级缓存》，谈到缓存不说一下一致性Hash算法那就是在耍流氓。 分布式缓存集群的访问模型 现在通常使用Redis来做分布式缓存，下面我们就以Redis为例： 假如当前我们系统的业务发展很快，需要缓存的数据很多，所以我们做了一个由三组主从复制的redis组成的高.
每天进步一点点——五分钟理解一致性哈希算法(consistent hashing)
热门推荐
Cynric 的博客
04-11 49万+
五分钟让你深入了解分布式系统中常用的一致性哈希算法
一致性哈希算法与Java实现
清晨
10-09 1万+
一致性哈希算法与Java实现 ======================================================== 一致性哈希算法是分布式系统中常用的算法。比如，一个分布式的存储系统，要将数据存储到具体的节点上， 如果采用普通的hash方法，将数据映射到具体的节点上，如key%N，key是数据的key，N是机器节点数， 如果有一个机器加入或退出这个集群，则所
一致性哈希算法学习及JAVA代码实现分析
weixin_34082177的博客
08-17 118
1，对于待存储的海量数据，如何将它们分配到各个机器中去？---数据分片与路由 当数据量很大时，通过改善单机硬件资源的纵向扩充方式来存储数据变得越来越不适用，而通过增加机器数目来获得水平横向扩展的方式则越来越流行。因此，就有个问题，如何将这些海量的数据分配到各个机器中？数据分布到各个机器存储之后，又如何进行查找？这里主要记录一致性Hash算法如何将数据分配到各个机器中去。   2，衡量一致性哈...
对一致性Hash算法，Java代码实现的深入研究
weixin_34235105的博客
02-13 214
一致性Hash算法 关于一致性Hash算法，在我之前的博文中已经有多次提到了，MemCache超详细解读一文中"一致性Hash算法"部分，对于为什么要使用一致性Hash算法、一致性Hash算法的算法原理做了详细的解读。 算法的具体原理这里再次贴上： 先构造一个长度为232的整数环（这个环被称为一致性Hash环），根据节点名称的Hash值（其分布为[0, 232-1]）将服务器节点放置在这个H...
一致性哈希算法 mysql_一致性哈希
weixin_42527464的博客
01-30 813
[TOC]前言伴随着系统流量的增大,出现了应用集群。在 Redis 中为了保证 Redis 的高可用也为 Redis 搭建了集群对数据进行分槽存放。在 Mysql数据库要存储的量达到一个很高的地步的时候,我们会对数据库进行分库分表操作。OK，到这儿先假设我们不知道什么是集群、什么是分库分表,我们先来看一个数据库水平切分演变的例子:假设我们的系统中有一张会员表 customer_info, 我们的系...
Ketama一致性Hash算法(含Java代码) 1
08-03
Ketama一致性哈希算法是基于一致性哈希的一种优化实现，主要解决了传统一致性哈希中节点分布不均匀的问题。在Ketama中，每个实际的物理服务器会被映射到多个虚拟节点，通常是100到200个，这些虚拟节点均匀分布在环上...
一致性哈希算法演示.rar
12-04
本压缩包文件"一致性哈希算法演示.rar"包含了一个C#实现的一致性哈希算法演示项目，可以在Visual Studio 2019环境下运行。该项目可以帮助我们理解一致性哈希的工作原理，通过观察不同情况下（如添加或移除节点）数据...
一致性哈希与Chord1
08-03
【一致性哈希与Chord1】是一篇关于分布式哈希算法的文章，主要讨论了一致性哈希和普通哈希的区别，以及如何通过引入...在Java等编程语言中，一致性哈希可以用于实现高效、灵活的分布式服务，如缓存系统、负载均衡器等。
ufire-springcloud-platform：基于一致性哈希算法实现websocket分布式扩展的尝试，提供模拟停机机演示解决单点故障演示，实现websocket服务的扩展容限。基于jenkins + github hook + docker-compose实现自动化持续部署
02-14
本文将探讨一个名为"ufire-springcloud-platform"的项目，该项目是基于一致性哈希算法实现WebSocket分布式扩展的一次尝试，并结合Jenkins、GitHub Hook和Docker Compose实现了自动化持续部署。 1. **一致性哈希算法...
一致性hashjava实现
12-10
别人写的一个一致性hash的java实现，分享下
JAVA实现一致性Hash算法
qq_49173222的博客
05-11 2826
介绍 一致性Hash算法是实现负载均衡的一种策略，后续会写如何实现负载均衡 一致哈希是一种特殊的哈希算法。 在使用一致哈希算法后，哈希表槽位数（大小）的改变平均只需要对 K/n个关键字重新映射，其中K是关键字的数量， n是槽位数量。 然而在传统的哈希表中，添加或删除一个槽位的几乎需要对所有关键字进行重新映射。 强哈希 考虑到单服务器不能承载，因此使用了分布式架构，最初的算法为 hash() mod n, hash()通常取用户ID，n为节点数。 此方法容易实现且能够满足运营要求。缺点是当单点发
一致性哈希java实现
一个码农的博客
03-03 851
该client采用TreeMap存储所有节点，模拟一个环形的逻辑关系。在这个环中，节点之前是存在顺序关系的，所以TreeMap的key必须实现Comparator接口。  那节点是怎样放入这个环中的呢？  Java代码   //对所有节点，生成nCopies个虚拟结点 for(Node node : nodes) { //每
一致性哈希算法 Java实现
Coding for freedom
04-10 1078
一致性哈希算法 虚拟节点 Java版本的简单实现。
Java实现一致性Hash算法
何忆清风
09-05 676
java实现一直Hash算法
一致性哈希 java实现_一致性哈希算法学习及JAVA代码实现分析
weixin_34638409的博客
02-12 305
1，对于待存储的海量数据，如何将它们分配到各个机器中去？---数据分片与路由当数据量很大时，通过改善单机硬件资源的纵向扩充方式来存储数据变得越来越不适用，而通过增加机器数目来获得水平横向扩展的方式则越来越流行。因此，就有个问题，如何将这些海量的数据分配到各个机器中？数据分布到各个机器存储之后，又如何进行查找？这里主要记录一致性Hash算法如何将数据分配到各个机器中去。2，衡量一致性哈希算法好处的四...
一致性hash java实现
练习时长1个月
09-11 665
前言 之前讲了 一致性hash算法的原理，现在撸代码。 环的数据结构，可能首先想到的是常用的List。一致性hash需要找比当前元素大的节点，那么list要么排好序然后比较找到对应的节点，要么是不排序直接遍历算差值。显然在这种查找比较频繁的场景树结构更适合，所以我们用有序的树结构TreeMap。 节点的hash冲突时我们再取一次hash值 /**一致性hash * Created by ...
一致性hash算法及java实现
青鱼入云的博客
03-28 1万+
一致性hash算法是分布式中一个常用且好用的分片算法、或者数据库分库分表算法。现在的互联网服务架构中，为避免单点故障、提升处理效率、横向扩展等原因，分布式系统已经成为了居家旅行必备的部署模式，所以也产出了几种数据分片的方法： 1.取模，2.划段，3.一致性hash 前两种有很大的一个问题就是需要固定的节点数，即节点数不能变，不能某一个节点挂了或者实时增加一个节点，变了分片规则就需要改变，需要迁...
一致性hash算法和Java实现
sunct的博客
02-23 793
一致性hash算法 一、前言 在大型web应用中，缓存可算是当今的一个标准开发配置了。在大规模的缓存应用中，应运而生了分布式缓存系统。在高并发（比如20W/S QPS + 海量数据）环境下，如何让请求均匀分散到集群中，防止应用数据库雪崩？ 二、Hash取模 基本原理 计算方式：hash(key) % 缓存集群节点数量 使用 这个算法的问题在于容错性和扩展性不好。所谓容错性是指当系统中某一个...
Ketama一致性哈希算法详解与Java实现，解决Memcached分布式负载均衡
Ketama一致性哈希算法是一种用于分布式系统中的负载均衡算法，尤其适用于像Memcached这样的键值存储服务。它避免了传统取模方法在增加或删除服务器时可能导致的性能下降问题，即同一键值可能会因为服务器变化而无法...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值