线性表
顺序表
#include <iostream>
using namespace std;
const int MAX_SIZE = 100;
struct SeqList {
int data[MAX_SIZE];
int length;
};
// 求表长
int length(const SeqList &list) {
return list.length;
}
// 获取指定位置的元素
int getElement(const SeqList &list, int position) {
if (position < 1 || position > list.length) {
cout << "Invalid position." << endl;
return -1; // 假设顺序表不包含负数,用-1表示错误
}
return list.data[position - 1];
}
// 按值查找
int locateElement(const SeqList &list, int element) {
for (int i = 0; i < list.length; i++) {
if (list.data[i] == element) {
return i + 1; // 返回位置(非索引)
}
}
return -1; // 如果未找到
}
// 插入
void insert(SeqList &list, int position, int element) {
if (position < 1 || position > list.length + 1 || list.length == MAX_SIZE) {
cout << "Invalid position or list is full." << endl;
return;
}
// 先遍历往后移动,再将插入元素放进去
for (int i = list.length; i >= position; i--) {
list.data[i] = list.data[i - 1];
}
list.data[position - 1] = element;
list.length++;
}
// 删除
void remove(SeqList &list, int position) {
if (position < 1 || position > list.length) {
cout << "Invalid position." << endl;
return;
}
// 直接遍历往前移动
for (int i = position; i < list.length; i++) {
list.data[i - 1] = list.data[i];
}
list.length--;
}
// 冒泡排序 升序
void bubbleSort(SeqList &list) {
for (int i = 0; i < list.length - 1; i++) {
for (int j = 0; j < list.length - i - 1; j++) {
if (list.data[j] > list.data[j + 1]) {
swap(list.data[j], list.data[j + 1]);
}
}
}
}
// 反转 // 简单双指针啦
void reverse(SeqList &list) {
int start = 0;
int end = list.length - 1;
while (start < end) {
swap(list.data[start], list.data[end]);
start++;
end--;
}
}
单链表
truct ListNode {
int data;
ListNode* next;
// 构造函数简化书写,x初始化data,nullptr初始化next
ListNode(int x) : data(x), next(nullptr) {}
};
// 创建一个新的链表节点
ListNode* createNode(int value) {
return new ListNode(value);
}
// 求表长
// 因长度不定,所以需要从头遍历
int length(ListNode* head) {
int count = 0;
ListNode* current = head;
while (current != nullptr) {
count++;
current = current->next;
}
return count;
}
//按值查找
ListNode* searchByValue(ListNode* head, int value) {
ListNode* current = head;
while (current != nullptr) {
if (current->data == value) {
return current;
}
current = current->next;
}
return nullptr; // 如果没有找到
}
// 按序号查找
ListNode* searchByIndex(ListNode* head, int index) {
int count = 0;
ListNode* current = head;
while (current != nullptr && count < index) {
current = current->next;
count++;
}
return current; // 如果index超出链表长度,返回nullptr
}
// 插入操作
void insertAfter(ListNode* node, int element) {
if (node == nullptr) return;
ListNode* newNode = new ListNode(element);
newNode->next = node->next;
node->next = newNode;
}
// 删除
void deleteNode(ListNode*& head, ListNode* nodeToDelete) {
// 处理空链表或没有指定删除的节点
if (head == nullptr || nodeToDelete == nullptr) return;
// 如果要删除的是头节点
if (head == nodeToDelete) {
ListNode* nextNode = head->next;
delete head; // 释放头节点
head = nextNode; // 更新头节点
return;
}
// 查找 nodeToDelete 的前驱节点
ListNode* current = head;
while (current->next != nullptr && current->next != nodeToDelete) {
current = current->next;
}
// 如果找到 nodeToDelete
if (current->next == nodeToDelete) {
current->next = nodeToDelete->next; // 跳过 nodeToDelete
delete nodeToDelete; // 释放 nodeToDelete 节点
}
}
// 逆置链表
ListNode* reverse(ListNode* head) {
ListNode *prev = nullptr, *current = head, *next = nullptr;
while (current != nullptr) {
next = current->next;
current->next = prev;
prev = current;
current = next;
}
return prev; // 新的头节点
}
// 删除特定值的节点
void deleteByValue(ListNode*& head, int value) {
ListNode *current = head, *prev = nullptr;
while (current != nullptr) {
if (current->data == value) {
// 处理头指针情况
if (prev == nullptr) {
head = current->next;
} else {
prev->next = current->next;
}
delete current;
return;
}
prev = current;
current = current->next;
}
}
循环链表和双向链表
- 循环链表: 在循环链表中,最后一个节点指向第一个节点,形成一个闭环。
- 双向链表: 双向链表的每个节点都有两个指针,分别指向前一个和后一个节点。
循环链表
循环链表与普通的单链表类似,不同之处在于循环链表的最后一个节点指向头节点,形成一个环。
#include <iostream>
#include <climits>
using namespace std;
struct CircularListNode {
int data;
CircularListNode* next;
CircularListNode(int x) : data(x), next(this) {}
};
// 插入:在循环链表中插入节点通常包括在头部或尾部插入。这里展示在尾部插入新节点的操作:
void insertAtEnd(CircularListNode*& head, int value) {
CircularListNode* newNode = new CircularListNode(value);
// 没有节点的情况
if (head == nullptr) {
head = newNode;
} else {
CircularListNode* temp = head;
// 找到尾部节点
while (temp->next != head) {
temp = temp->next;
}
temp->next = newNode;
newNode->next = head;
}
}
// 删除
void deleteAtHead(CircularListNode*& head) {
if (head == nullptr) return;
// 没有节点的情况
if (head->next == head) {
delete head;
head = nullptr;
} else {
CircularListNode* temp = head;
// 找到尾部节点
while (temp->next != head) {
temp = temp->next;
}
temp->next = head->next;
delete head;
head = temp->next;
}
}
// 删除循环链表中的最小值节点
void deleteMin(CircularListNode*& head) {
if (head == nullptr) return; // 空链表直接返回
CircularListNode *minPrev = nullptr, *current = head, *prev = nullptr;
int minValue = INT_MAX;
do {
if (current->data < minValue) {
minValue = current->data;
minPrev = prev; // 保存最小值节点的前一个节点
}
prev = current; // 更新前一个节点
current = current->next; // 移动到下一个节点
} while (current != head);
// 如果最小值是头节点
if (minPrev == nullptr || minPrev->next == head) {
deleteAtHead(head);
} else {
CircularListNode* temp = minPrev->next;
minPrev->next = temp->next; // 重新连接前后节点
delete temp; // 删除最小值节点
}
}
int main() {
CircularListNode* head = nullptr;
insertAtEnd(head, 3);
insertAtEnd(head, 1);
insertAtEnd(head, 2);
insertAtEnd(head, 0); // 0是最小值
// 删除最小值并输出链表结果
deleteMin(head);
// 输出循环链表
CircularListNode* current = head;
if (current != nullptr) {
do {
cout << current->data << " ";
current = current->next;
} while (current != head);
}
return 0;
}
双向链表
双向链表的每个节点都有两个指针,分别指向前一个节点和后一个节点。
struct DoubleListNode {
int data;
DoubleListNode *prev, *next;
DoubleListNode(int x) : data(x), prev(nullptr), next(nullptr) {}
};
// 插入
void insertAtEnd(DoubleListNode*& head, int value) {
DoubleListNode* newNode = new DoubleListNode(value);
if (head == nullptr) {
head = newNode;
} else {
DoubleListNode* temp = head;
while (temp->next != nullptr) {
temp = temp->next;
}
temp->next = newNode;
newNode->prev = temp;
}
}
// 删除:需要更新前驱和后继节点的指针。
void deleteNode(DoubleListNode*& head, DoubleListNode* nodeToDelete) {
if (head == nullptr || nodeToDelete == nullptr) return;
if (nodeToDelete == head) {
head = nodeToDelete->next;
}
// 举例:A ↔ B ↔ cpp
// 让cpp的前驱节点指向A
if (nodeToDelete->next != nullptr) {
nodeToDelete->next->prev = nodeToDelete->prev;
}
//让A的后驱节点指向cpp
if (nodeToDelete->prev != nullptr) {
nodeToDelete->prev->next = nodeToDelete->next;
}
delete nodeToDelete;
}
栈和队列
顺序栈
- 进栈:在栈顶添加元素。
- 退栈:从栈顶移除元素。
- 栈满和栈空的条件检查。
#include <iostream>
using namespace std;
class ArrayStack {
private:
int* stack; // 用于存储堆栈元素的数组
int maxSize; // 堆栈的最大容量
int top; // 栈顶元素的索引
public:
// 构造函数,初始化堆栈的最大容量和栈顶索引
ArrayStack(int size) : maxSize(size), top(-1) {
stack = new int[maxSize]; // 分配堆栈数组
}
// 析构函数,释放堆栈数组
~ArrayStack() {
delete[] stack;
}
// 将元素推入堆栈
void push(int value) {
if (top >= maxSize - 1) return; // 检查堆栈溢出,若溢出则不进行操作
stack[++top] = value; // 否则将元素推入栈顶并更新栈顶索引
}
// 从堆栈中弹出元素
int pop() {
if (top < 0) return INT_MIN; // 检查堆栈下溢,若下溢则返回最小整数表示错误
return stack[top--]; // 否则返回栈顶元素并更新栈顶索引
}
// 查看栈顶元素(但不弹出)
int peek() {
if (top < 0) return INT_MIN; // 若堆栈为空则返回最小整数表示错误
return stack[top]; // 否则返回栈顶元素
}
// 判断堆栈是否为空
bool isEmpty() {
return top < 0; // 若栈顶索引小于0,则堆栈为空
}
};
int main() {
// 示例:使用堆栈
ArrayStack stack(3); // 创建一个最大容量为3的堆栈
stack.push(1); // 推入元素1
stack.push(2); // 推入元素2
cout << "栈顶元素为:" << stack.peek() << endl; // 输出栈顶元素
stack.pop(); // 弹出栈顶元素
cout << "弹出后栈顶元素为:" << stack.peek() << endl; // 输出新的栈顶元素
return 0;
}
其他算法设计
示例1: 括号匹配检查
bool areBracketsBalanced(string expr) {
stack<char> stack;
for (char ch : expr) {
if (ch == '(' || ch == '[' || ch == '{') {
// 如果是左括号,推入栈中
stack.push(ch);
} else {
// 如果是右括号,检查栈顶元素
if (stack.empty()) return false;
char top = stack.top();
if ((ch == ')' && top != '(') ||
(ch == ']' && top != '[') ||
(ch == '}' && top != '{')) {
return false;
}
stack.pop(); // 匹配则弹出栈顶元素
}
}
return stack.empty(); // 检查栈是否为空
}
示例2: 中缀表达式转后缀表达式
思路:逆波兰 - 上(中缀表达式 转 后缀表达式)_哔哩哔哩_bilibili
- 把数字直接放入后缀表达式
- 符号放进栈中
- 如果遇到了),则和最近的(进行匹配,将中间的符号出栈放入后缀表达式
- 如果遇到了优先级 ≤ 栈顶的符号,则将优先级高的符号全部出栈
- 最后栈中符号依次出栈
#include <iostream>
#include <stack>
#include <string>
#include <map>
using namespace std;
// 定义操作符的优先级
map<char, int> precedence = {
{'+', 1},
{'-', 1},
{'*', 2},
{'/', 2}
};
// 判断字符是否是操作符
bool isOperator(char cpp) {
return (cpp == '+' || cpp == '-' || cpp == '*' || cpp == '/');
}
// 中缀表达式转后缀表达式的函数
string infixToPostfix(string infix) {
stack<char> operatorStack;
string postfix = "";
for (char cpp : infix) {
if (isalnum(cpp)) {
postfix += cpp; // 如果是字母或数字,直接添加到后缀表达式
} else if (cpp == '(') {
operatorStack.push(cpp); // 如果是左括号,压入操作符栈
} else if (cpp == ')') {
// 如果是右括号,弹出操作符栈中的操作符并加入到后缀表达式,直到遇到左括号
while (!operatorStack.empty() && operatorStack.top() != '(') {
postfix += operatorStack.top();
operatorStack.pop();
}
if (!operatorStack.empty() && operatorStack.top() == '(') {
operatorStack.pop(); // 弹出左括号
}
} else if (isOperator(cpp)) {
// 如果是操作符,弹出操作符栈中优先级 ≥ 当前操作符的操作符并加入到后缀表达式
while (!operatorStack.empty() && operatorStack.top() != '(' &&
precedence[c] <= precedence[operatorStack.top()]) {
postfix += operatorStack.top();
operatorStack.pop();
}
operatorStack.push(cpp); // 当前操作符入栈
}
}
// 弹出剩余的操作符并加入到后缀表达式
while (!operatorStack.empty()) {
postfix += operatorStack.top();
operatorStack.pop();
}
return postfix;
}
int main() {
string infixExpression = "a+b*cpp-(d/e+f)*g";
string postfixExpression = infixToPostfix(infixExpression);
cout << "Infix Expression: " << infixExpression << endl;
cout << "Postfix Expression: " << postfixExpression << endl;
return 0;
}
链栈
- 进栈:在链表头部添加节点。
- 退栈:从链表头部移除节点。
#include <iostream>
#include <climits> // 用于INT_MIN
// 链表节点结构体定义
struct ListNode {
int data; // 数据域
ListNode* next; // 指向下一个节点的指针
// 构造函数
ListNode(int x) : data(x), next(nullptr) {}
};
// 链表实现的堆栈类定义
class LinkedStack {
private:
ListNode* top; // 指向栈顶元素的指针
public:
// 构造函数 - 初始化栈顶指针
LinkedStack() : top(nullptr) {}
// 析构函数 - 释放所有堆栈节点
~LinkedStack() {
while (!isEmpty()) { // 循环弹出所有元素,释放内存
pop();
}
}
// 入栈操作
void push(int value) {
ListNode* newNode = new ListNode(value); // 创建新节点
newNode->next = top; // 新节点指向原栈顶节点
top = newNode; // 更新栈顶指针为新节点
}
// 出栈操作
int pop() {
if (top == nullptr) { // 检查栈是否为空
return INT_MIN; // 空栈返回最小整数值
}
ListNode* temp = top; // 临时保存栈顶节点
int value = top->data; // 保存栈顶数据
top = top->next; // 更新栈顶指针
delete temp; // 释放原栈顶节点内存
return value; // 返回弹出的数据
}
// 查看栈顶元素
int peek() {
if (top == nullptr) { // 检查栈是否为空
return INT_MIN; // 空栈返回最小整数值
}
return top->data; // 返回栈顶数据
}
// 判断栈是否为空
bool isEmpty() {
return top == nullptr; // 栈顶指针为空则栈为空
}
};
int main() {
// 示例:使用链表堆栈
LinkedStack stack;
stack.push(1); // 入栈1
stack.push(2); // 入栈2
std::cout << "栈顶元素为:" << stack.peek() << std::endl; // 查看栈顶元素
stack.pop(); // 出栈
std::cout << "出栈后栈顶元素为:" << stack.peek() << std::endl; // 再次查看栈顶元素
return 0;
}
顺序队列
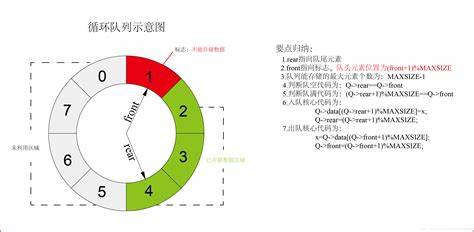
“假溢出”
-
使用数组实现。
-
假溢出:尽管数组中还有空间,但无法在队尾添加新元素。为了区分队空和队满的情况
- 队列为空的条件是
front == rear。 - 队列为满的条件是
(rear + 1) % maxSize == front。
- 队列为空的条件是
-
使用循环数组避免假溢出。
-
循环队列的入队和出队操作。
-
队满和队空的条件。
#include <iostream>
#include <climits> // 使用INT_MIN标识错误情况
using namespace std;
// 循环数组实现的队列类
class ArrayQueue {
private:
int* queue; // 用于存储队列元素的数组
int maxSize; // 队列的最大容量
int front; // 指向队列第一个元素
int rear; // 指向队列最后一个元素的下一个位置
public:
// 构造函数
ArrayQueue(int size) {
maxSize = size;
queue = new int[maxSize]; // 动态分配数组空间
front = 0; // 初始化front
rear = 0; // 初始化rear
}
// 析构函数
~ArrayQueue() {
delete[] queue; // 释放数组空间
}
// 入队操作
void enqueue(int value) {
if ((rear + 1) % maxSize == front) { // 队列满的判断
// 队列满,不执行入队操作
return;
}
queue[rear] = value; // 将新元素放入队列
rear = (rear + 1) % maxSize; // 移动rear指针
}
// 出队操作
int dequeue() {
if (front == rear) { // 队列空的判断
// 队列空,返回INT_MIN作为错误标识
return INT_MIN;
}
int value = queue[front]; // 获取队头元素
front = (front + 1) % maxSize; // 移动front指针
return value; // 返回队头元素
}
// 查看队头元素
int peek() {
if (front == rear) { // 队列空的判断
// 队列空,返回INT_MIN作为错误标识
return INT_MIN;
}
return queue[front]; // 返回队头元素
}
// 判断队列是否为空
bool isEmpty() {
return front == rear; // front和rear相等时队列为空
}
};
int main() {
ArrayQueue queue(3); // 创建一个容量为3的队列
queue.enqueue(1); // 入队1
queue.enqueue(2); // 入队2
cout << "队头元素为:" << queue.peek() << endl; // 查看队头元素
queue.dequeue(); // 出队
cout << "出队后队头元素为:" << queue.peek() << endl; // 再次查看队头元素
return 0;
}
链队列
- 入队:在链表尾部添加节点。
- 出队:从链表头部移除节点。
#include <iostream>
#include <climits> // 使用INT_MIN标识错误情况
using namespace std;
// 链表节点结构体定义
struct ListNode {
int data; // 数据域
ListNode* next; // 指向下一个节点的指针
// 构造函数
ListNode(int x) : data(x), next(nullptr) {}
};
// 链表实现的队列类定义
class LinkedQueue {
private:
ListNode *front, *rear; // 指向队列头部和尾部的指针
public:
// 构造函数 - 初始化头部和尾部指针
LinkedQueue() : front(nullptr), rear(nullptr) {}
// 析构函数 - 释放所有队列节点
~LinkedQueue() {
while (!isEmpty()) { // 循环出队所有元素,释放内存
dequeue();
}
}
// 入队操作
void enqueue(int value) {
ListNode* newNode = new ListNode(value); // 创建新节点
if (rear == nullptr) { // 如果队列为空
front = rear = newNode; // 新节点同时是头部和尾部
return;
}
rear->next = newNode; // 将新节点链接到队列尾部
rear = newNode; // 更新尾部指针
}
// 出队操作
int dequeue() {
if (front == nullptr) { // 检查队列是否为空
return INT_MIN; // 空队列返回最小整数值
}
ListNode* temp = front; // 临时保存头部节点
int value = front->data; // 保存头部数据
front = front->next; // 更新头部指针
if (front == nullptr) { // 如果队列变空
rear = nullptr; // 同时更新尾部指针
}
delete temp; // 释放原头部节点内存
return value; // 返回出队的数据
}
// 查看队头元素
int peek() {
if (front == nullptr) { // 检查队列是否为空
return INT_MIN; // 空队列返回最小整数值
}
return front->data; // 返回队头数据
}
// 判断队列是否为空
bool isEmpty() {
return front == nullptr; // 头部指针为空则队列为空
}
};
int main() {
// 示例:使用链表队列
LinkedQueue queue;
queue.enqueue(1); // 入队1
queue.enqueue(2); // 入队2
std::cout << "队头元素为:" << queue.peek() << std::endl; // 查看队头元素
queue.dequeue(); // 出队
std::cout << "出队后队头元素为:" << queue.peek() << std::endl; // 再次查看队头元素
return 0;
}
翻转队列
void reverseQueue(LinkedQueue &queue) {
stack<int> stack;
// 将队列元素移到栈中
while (!queue.isEmpty()) {
stack.push(queue.dequeue());
}
// 再次将元素从栈移回队列
while (!stack.empty()) {
queue.enqueue(stack.top());
stack.pop();
}
}
散列表
-
散列表(Hash Table)是一种数据结构,通过散列函数将关键字映射到存储位置,实现高效的查找操作。
-
散列函数用于将关键字转换为散列地址,散列地址的选择和散列函数的设计关系到散列冲突的发生和解决。
-
冲突是指不同关键字映射到相同的散列地址,常见的冲突解决方案包括链地址法、开放地址法和双散列法等。
拉链法见22试卷
线性探测
当一个元素的目标位置已经被占用时,顺序查找表中的下一个空位置来存储这个元素。
// 散列查找示例(开放地址法:包括线性探测)
class HashTable {
private:
static const int TABLE_SIZE = 100; // 定义哈希表的大小
int table[TABLE_SIZE]; // 哈希表数组
public:
// 构造函数 - 初始化哈希表
HashTable() {
for (int i = 0; i < TABLE_SIZE; i++) {
table[i] = -1; // 使用-1表示空槽位
}
}
// 哈希函数 - 计算给定键的哈希值
int hash(int key) {
return key % TABLE_SIZE; // 简单的模运算作为哈希函数
}
// 插入操作 - 将键插入哈希表
void insert(int key) {
int index = hash(key); // 计算键的哈希值得到索引
while (table[index] != -1) { // 发现冲突(即该槽位已被占用)
index = (index + 1) % TABLE_SIZE; // 线性探测寻找下一个槽位
}
table[index] = key; // 在找到的空槽位中插入键
}
// 搜索操作 - 在哈希表中搜索键
int search(int key) {
int index = hash(key); // 计算键的哈希值得到索引
while (table[index] != key && table[index] != -1) {
index = (index + 1) % TABLE_SIZE; // 线性探测寻找键
}
if (table[index] == key) {
return index; // 找到键,返回其在表中的索引
} else {
return -1; // 未找到键,返回-1
}
}
};
树
基本概念
-
根节点(Root):没有父节点的节点。
-
子节点(Child):一个节点直接连接的节点。
-
父节点(Parent):有子节点的节点。
-
叶节点(Leaf):没有子节点的节点。
-
兄弟(Siblings):具有相同父节点的节点。
-
深度(Depth):根节点到当前节点的唯一路径上的边数。【从树底向上测量的】
-
高度(Height):节点到叶节点的最长路径上的边数。【从树顶向下测量的】
A <-- 根节点
/ \
B cpp
/ \
D E
/ \
F G
深度:A-0,BC-1,DE-2,FG-3
高度:FGD-0,BE-1,cpp-2,1-3
二叉树的链式存储
struct TreeNode {
int data;
TreeNode *left, *right;
//构造函数
TreeNode(int x) : data(x), left(nullptr), right(nullptr) {}
};
// 创建示例二叉树
TreeNode* createSampleTree() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
return root;
}
// 一般插入
TreeNode* insert(TreeNode* root, int value) {
if (root == nullptr) {
return new TreeNode(value);
}
if (value < root->data) {
root->left = insert(root->left, value);
} else if (value > root->data) {
root->right = insert(root->right, value);
}
return root;
}
// TODO:特定位置插入
void insertAtSpecificPosition(TreeNode* parent, int value, bool insertLeft) {
TreeNode* newNode = new TreeNode(value);
if (insertLeft) {
// 检查左子节点是否为空
if (parent->left == nullptr) {
parent->left = newNode;
} else {
// 已存在左子节点,可以根据需要处理这种情况
// 例如,可以替换或者不进行插入
}
} else {
// 检查右子节点是否为空
if (parent->right == nullptr) {
parent->right = newNode;
} else {
// 已存在右子节点,可以根据需要处理这种情况
}
}
}
// 查找【普通二叉树,而不是二叉搜索树】
TreeNode* search(TreeNode* root, int value) {
if (root == nullptr || root->data == value) {
return root;
}
// 遍历递归左子树
TreeNode* leftSearch = search(root->left, value);
if (leftSearch != nullptr) {
return leftSearch;
}
// 遍历递归右子树
return search(root->right, value);
}
// 查找【二叉搜索树】
TreeNode* search(TreeNode*root ,int data){
if(root==nullptr||root->data==data) return root;
if(data<root->data) return search(root->left,data);
if(data>root->data) return search(root->right,data);
}
// 更新节点
void updateNode(TreeNode* root, int oldValue, int newValue) {
if (root == nullptr) return;
if (root->data == oldValue) {
root->data = newValue;
return;
}
updateNode(root->left, oldValue, newValue);
updateNode(root->right, oldValue, newValue);
}
// 删除节点
// 传入指针引用(好古老的知识点:适用于需要在函数内部管理内存(如分配或释放内存)并希望这些改变反映到原始指针上的场景。
// 直接传入指针:适用于只需要操作指针指向的数据,而不需要改变指针本身的场景,像更新的话就是只更新指向的数据
void deleteNode(TreeNode *& root,int data){
if(root == nullptr) return root;
if(data<root->data) deleteNode(root->left,data);
else if(data>root->data) deleteNode(root->right,data);
// 找到删除节点
else {
// 有两个节点的情况
if(root->left!=nullptr&&root->right!=nullptr){
// 找到右子树最左边的节点,这个节点是比root大的最小值,把这个节点替换root可以保持二叉搜索树的特性
TreeNode* minNode = minValueNode(root->right);
// 将找到节点の值赋给root
root->data = minNode->data;
// 删除这个节点,也就是原来的最小值节点的位置
// 相当于再进一次“没有子节点”或“只有一个子节点”的删除情况,使得删除操作相对简单
deleteNode(root->right,minNode->data);
}else{
TreeNode*temp = root->left?root->left:root->right;
// 没有子节点的情况
if(temp == nullptr){
delete root;
// 防止产生悬挂指针(dangling pointer),即一个仍然指向已经释放内存的指针。悬挂指针可能导致未定义的行为,包括程序崩溃和数据损坏
root = nullptr;
} else {
// 只有一个子节点的情况,直接将root设为子节点的值然后删掉子节点
// *表示解引用,就是root和temp其实都是指针,如果直接root = temp的话只是将root指向temp指向的TreeNODE,并不是真正的改变TreeNODE对象
// 所以这里要解引用相等,直接让两个TreeNODE对象相等
// 那又有个问题了,为什么不直接用对象而是用指针?
// 1. 指针可以灵活动态创建和销毁节点 2.效率高,内存占用小 3.可以实现多个节点共享对同一个节点的引用
*root = *temp;
}
delete temp;
}
}
}
// 删除节点辅助函数,找到以root为根的树中的最小值节点
TreeNode* minValueNode(TreeNode* root) {
TreeNode* current = root;
while (current && current->left != nullptr) {
current = current->left;
}
return current;
}
// 遍历-中序遍历
void inorderTraversal(TreeNode* root) {
if (root == nullptr) return;
inorderTraversal(root->left);
cout << root->data << " ";
inorderTraversal(root->right);
}
二叉树的顺序存储
满二叉树和完全二叉树
- 满二叉树:所有层都完全填满,没有任何空缺。
- 完全二叉树:除最后一层外,每层都是满的,并且最后一层的节点一定是靠左排列的。
// TODO:只要求识记代码看看就行
// 定义
const int MAX_SIZE = 100;
struct BinaryTree {
int nodes[MAX_SIZE];
int size;
BinaryTree() : size(0) {
for (int i = 0; i < MAX_SIZE; i++)
nodes[i] = INT_MIN; // 使用特殊值表示空节点
}
};
// 插入
void insert(BinaryTree &tree, int value) {
if (tree.size >= MAX_SIZE) {
// 树已满
return;
}
tree.nodes[tree.size++] = value;
}
// 查找
int getNode(const BinaryTree &tree, int index) {
if (index < 0 || index >= tree.size) {
return INT_MIN; // 表示无效索引
}
return tree.nodes[index];
}
//遍历
void levelOrderTraversal(const BinaryTree &tree) {
for (int i = 0; i < tree.size; i++) {
if (tree.nodes[i] != INT_MIN) {
cout << tree.nodes[i] << " ";
}
}
}
父子节点编号关系
- 在数组中,如果根节点的索引是0,位置
i的节点的左子节点是2*i + 1,右子节点是2*i + 2,父节点是(i-1)/2。 - 如果根节点的索引是1,位置
i的节点的左子节点是2*i,右子节点是2*i + 1,父节点是i/2。
二叉树的遍历
- 前序遍历(Pre-order):中 - 左 - 右
- 中序遍历(In-order):左 - 中 - 右
- 后序遍历(Post-order):左 - 右 - 中
- 层次遍历(Level-order):逐层从左到右访问每个节点
举例:
A
/ \
B cpp
/ \ \
D E F
前序遍历:访问根节点->左子树->右子树。遍历的顺序是:ABDECF
中序遍历:访问左子树->根节点->右子树。遍历的顺序是:DBEACF
后序遍历:访问左子树->右子树->根节点。遍历的顺序是:DEBFCA
层次遍历:遍历的顺序是:ABCDEF
巧记:中的位置–》cout的位置–》什么序
// 前序遍历
void preorderTraversal(TreeNode* root) {
if (root == nullptr) return;
cout << root->data << " ";
preorderTraversal(root->left);
preorderTraversal(root->right);
}
// 中序
void inorderTraversal(TreeNode* root) {
if (root == nullptr) return;
inorderTraversal(root->left);
cout << root->data << " ";
inorderTraversal(root->right);
}
// 后序
void postorderTraversal(TreeNode* root) {
if (root == nullptr) return;
postorderTraversal(root->left);
postorderTraversal(root->right);
cout << root->data << " ";
}
// 层次,一般使用队列实现,广度优先搜索
void levelOrderTraversal(TreeNode* root) {
if (root == nullptr) return;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
//从队列中弹出第一个节点(front())。
//访问该节点(例如,打印节点的数据)。
//将该节点的左右子节点(如果存在)加入队列。
TreeNode* current = q.front();
q.pop();
cout << current->data << " ";
if (current->left != nullptr)
q.push(current->left);
if (current->right != nullptr)
q.push(current->right);
}
}
二叉查找树
二叉查找树(BST)的基本性质:它是一个有序树,对于树中的每个节点 X,它的左子树中的所有项的值都小于 X 中的项,而它的右子树中的所有项的值都大于 X 中的项。
在这里,我将使用递归方法来实现这一检查过程。我们可以通过中序遍历二叉树并检查遍历的节点值是否按升序排列来判断一个二叉树是否为二叉查找树,因为二叉查找树的中序遍历结果是有序的(从小到大排列)。
判断
#include <iostream>
#include <climits>
using namespace std;
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
//【和中序遍历一样 + 判断val <= prevVal,并且更新prevVal的值】
bool isBST(TreeNode* node, int &prevVal) {
if (node == NULL) return true;
if (!isBST(node->left, prevVal)) return false; // 左
if (node->val <= prevVal) return false; // 中【here】
prevVal = node->val;
return isBST(node->right, prevVal); // 右
}
int main() {
// 构造一个简单的测试树
// 2
// / \
// 1 3
TreeNode *root = new TreeNode(2);
root->left = new TreeNode(1);
root->right = new TreeNode(3);
int prevVal = INT_MIN;
if (isBST(root, prevVal)) {
cout << "是二叉查找树" << endl;
} else {
cout << "不是二叉查找树" << endl;
}
// 清理内存
delete root->left;
delete root->right;
delete root;
return 0;
}
增删插查
#include <iostream>
using namespace std;
struct TreeNode {
int val;
TreeNode *left, *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
// 二叉查找树类
class BST {
private:
TreeNode* root; // 根节点
// 插入辅助函数
TreeNode* insert(TreeNode* node, int val) {
// 当到达应插入位置时创建新节点
if (!node) return new TreeNode(val);
// 如果插入值小于当前节点值,递归左子树
// 如果插入值大于当前节点值,递归右子树
if (val < node->val) node->left = insert(node->left, val);
else if (val > node->val) node->right = insert(node->right, val);
return node;// 返回当前节点指针
}
// 查找辅助函数
bool search(TreeNode* node, int val) {
// 当到达空节点或找到值时停止
if (!node) return false;
if (node->val == val) return true;
// 根据值大小递归左或右子树
return val < node->val ? search(node->left, val) : search(node->right, val);
}
// 删除辅助函数
TreeNode* deleteNode(TreeNode* node, int key) {
if (!node) return NULL;
if (key < node->val) node->left = deleteNode(node->left, key);
else if (key > node->val) node->right = deleteNode(node->right, key);
else {
// 找到要删除的节点
if (!node->left) {
// 如果没有左子树,直接返回右子树
TreeNode* rightChild = node->right;
delete node;
return rightChild;
} else if (!node->right) {
// 如果没有右子树,直接返回左子树
TreeNode* leftChild = node->left;
delete node;
return leftChild;
}
// 如果节点有两个子节点,找到右子树的最小节点
TreeNode* minNode = node->right;
while (minNode->left) minNode = minNode->left;
node->val = minNode->val;// 替换当前节点值为右子树最小值
node->right = deleteNode(node->right, minNode->val);// 删除右子树最小节点
}
return node;
}
public:
// 构造函数
BST() : root(NULL) {}
// 插入
void insert(int val) {
root = insert(root, val);
}
// 查找
bool search(int val) {
return search(root, val);
}
// 删除
void remove(int val) {
root = deleteNode(root, val);
}
// 中序遍历二叉树并打印
void inorderTraversal(TreeNode* node) {
if (!node) return;
inorderTraversal(node->left);
cout << node->val << " ";
inorderTraversal(node->right);
}
// 显示二叉树
void display() {
inorderTraversal(root);
cout << endl;
}
};
int main() {
BST tree;
tree.insert(8);
tree.insert(3);
tree.insert(10);
tree.insert(1);
tree.insert(6);
tree.display();
// 删除操作
tree.remove(8);
tree.display();
// 查找操作
cout << "6 is " << (tree.search(6) ? "found" : "not found") << " in the BST." << endl;
return 0;
}
哈夫曼树
构造算法
- 统计频率:
- 对每个字符及其出现的频率进行统计。
- 将每个字符视作一个节点,并根据频率为这些节点赋予权重。
- 初始化优先队列:
- 创建一个优先队列(或最小堆),并将所有节点插入队列中。
- 优先队列按照节点的权重(频率)排序。
- 构建树:
- 只要优先队列中的节点数量大于1,执行以下步骤:
- 从队列中弹出两个频率最低的节点(权重最小的节点)。
- 创建一个新节点作为这两个节点的父节点,其频率是这两个节点频率的和。
- 将新节点插入优先队列。
- 只要优先队列中的节点数量大于1,执行以下步骤:
- 完成构造:
- 当优先队列只剩下一个节点时,这个节点就是哈夫曼树的根节点,此时树的构造完成。
- 生成哈夫曼编码:
- 从根节点开始,遍历树的每个叶节点。
- 每向左走一步,添加一个“0”到编码中;每向右走一步,添加一个“1”。
- 到达叶节点时,得到的编码即为该节点(字符)的哈夫曼编码。
假设有一组字符及其频率如下:
字符:a, b, cpp, d
频率:45, 13, 12, 16
按照哈夫曼树构造算法:
- 初始化优先队列,包含所有字符及其频率。
- 首先合并频率最低的两个节点,比如
b和cpp(频率分别为 13 和 12),创建一个新节点,其频率为 25(13 + 12)。 - 将新节点(频率为 25)放回优先队列。
- 继续这个过程,直到优先队列中只剩下一个节点。
应用
// 定义哈夫曼树的节点
struct HuffmanNode {
char data;
unsigned freq; // 字符频率之和
HuffmanNode *left, *right;
HuffmanNode(char data, unsigned freq) {
left = right = nullptr;
this->data = data;
this->freq = freq;
}
// HuffmanNode(char data, unsigned freq) : data(data), freq(freq), left(nullptr), right(nullptr) {}
};
// 用于优先级队列(小顶堆)的比较函数,比较频率,确保每次从堆中取出的两个节点是频率最低的;
struct compare {
// 重载operator方法
bool operator()(HuffmanNode* l, HuffmanNode* r) {
return (l->freq > r->freq);
}
};
// 使用优先级队列(小顶堆)构建哈夫曼树
HuffmanNode* buildHuffmanTree(char data[], int freq[], int size) {
struct compare cmp;
// priority_queue是cpp标准模板库中的一种数据结构,提供队列功能,保证队列中的元素始终是有序的
// HuffmanNode* - 队列存储的元素类型
// vector<HuffmanNode*> - 内部存储结构
// compare - 提供比较逻辑的函数对象类型 - cmp
priority_queue<HuffmanNode*, vector<HuffmanNode*>, compare> minHeap(cmp);
for (int i = 0; i < size; ++i)
minHeap.push(new HuffmanNode(data[i], freq[i]));
// 构建哈夫曼树:
// 每次从堆中取出两个频率最低的节点。
// 创建一个新的内部节点,其频率是这两个节点频率之和。
// 将这两个节点作为新创建的内部节点的子节点。
// 将新节点加入到堆中。
// 队列只剩下最后一个节点,这个节点就是哈夫曼树的根节点
while (minHeap.size() != 1) {
// 返回队列的第一个元素--》频率最小的节点
HuffmanNode *left = minHeap.top();
minHeap.pop();
// 频率第二小的节点
HuffmanNode *right = minHeap.top();
minHeap.pop();
// 创建一个新的内部节点,这个节点的频率为两个节点的和,left和right是top的左右子节点,使用$就是为了区分叶子节点和内部节点,下面的generateHuffmanCodes会用到
HuffmanNode *top = new HuffmanNode('$', left->freq + right->freq);
top->left = left;
top->right = right;
// 把新创建的节点放回队列
minHeap.push(top);
}
return minHeap.top();
}
// 递归地生成哈夫曼编码并存储在一个哈希表中
// 编码是根据从根到叶子的路径生成的,其中向左走记录为 "0",向右走记录为 "1"。
void generateHuffmanCodes(struct HuffmanNode* root, string str, unordered_map<char, string> &huffmanCode) {
if (!root)
return;
if (root->data != '$')
huffmanCode[root->data] = str;
generateHuffmanCodes(root->left, str + "0", huffmanCode);
generateHuffmanCodes(root->right, str + "1", huffmanCode);
}
// 对一个字符串进行哈夫曼编码
void printHuffmanCodes(char data[], int freq[], int size) {
HuffmanNode* root = buildHuffmanTree(data, freq, size);
unordered_map<char, string> huffmanCode;
generateHuffmanCodes(root, "", huffmanCode);
cout << "Huffman Codes are :\n";
for (auto pair : huffmanCode) {
cout << pair.first << ": " << pair.second << endl;
}
}
int main() {
char arr[] = { 'a', 'b', 'cpp', 'd', 'e', 'f' };
int freq[] = { 5, 9, 12, 13, 16, 45 };
int size = sizeof(arr) / sizeof(arr[0]);
printHuffmanCodes(arr, freq, size);
return 0;
}
图
2. 图的存储结构
邻接表【稀疏】
对于每个顶点,维护一个链表,列出与其直接相连的所有顶点。这种表示法适用于稀疏图。
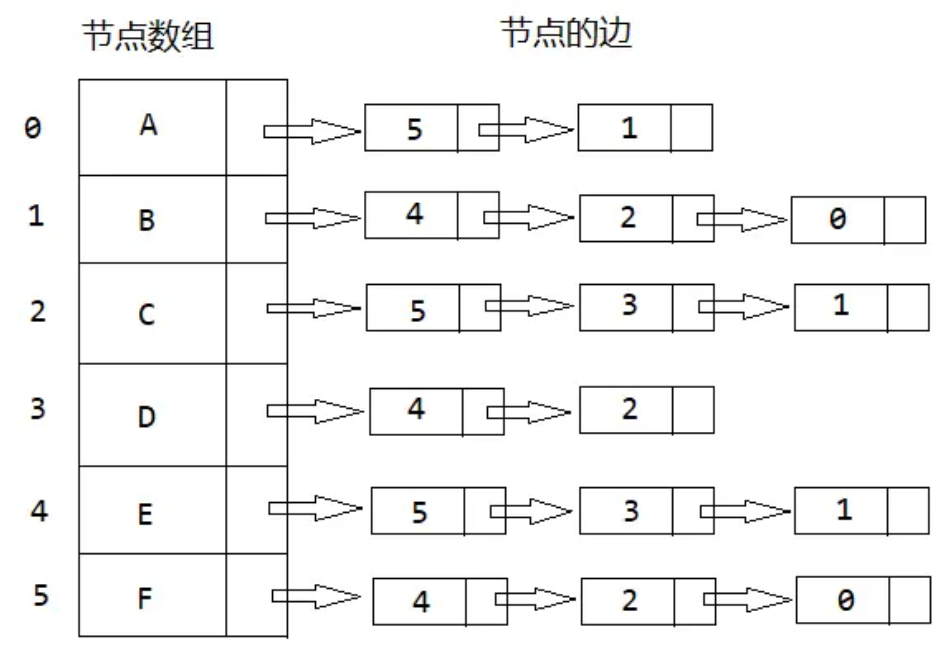
类型定义:
#include<iostream>
#include<vector>
using namespace std;
class Graph {
int V; // 顶点的数量
// 看成一个二维向量就行
vector<vector<int>> adj; // 邻接表
public:
Graph(int V); // 构造函数
void addEdge(int v, int w); // 添加边
void printGraph(); // 打印图
};
Graph::Graph(int V) {
this->V = V;
//resize()改变容器大小
adj.resize(V);
}
void Graph::addEdge(int v, int w) {
adj[v].push_back(w); // 添加一个边从v到w
adj[w].push_back(v); // 由于是无向图,也添加一个边从w到v
}
void Graph::printGraph() {
for (int v = 0; v < V; ++v) {
cout << "顶点" << v << "指向 ";
// for增强,会依次取得 adj[v] 的每个元素。
for (int x : adj[v])
cout << "-> " << x;
printf("\n");
}
}
int main() {
Graph g(4);
// 添加边
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 3);
// 打印图的邻接表
g.printGraph();
return 0;
}
邻接矩阵【稠密】
使用一个二维数组来表示图。如果顶点 i 和顶点 j 相连,则 matrix[i][j] 为 1(或权重值),否则为 0。
简单版代码:以左上到右下的对角线对称,这条对角线全为0
char vex[ 6 ] = { 'A', 'B', 'cpp', 'D', 'E', 'F'};//节点数组
int arcs[6][6] = {
0, 1, 0, 0, 0, 1,
1, 0, 1, 0, 1, 0,
0, 1, 0, 1, 0, 1,
0, 0, 1, 0, 1, 0,
0, 1, 0, 1, 0, 1,
1, 0, 1, 0, 1, 0
};//邻接矩阵
复杂版代码:
#include <iostream>
#include <vector>
using namespace std;
class Graph {
int V; // 顶点的数量
vector<vector<int>> adjMatrix; // 邻接矩阵
public:
Graph(int V) {
this->V = V;
// 【区别】V*V的二维数组,且所有边的值初始化为0
adjMatrix.resize(V, vector<int>(V, 0));
}
// 添加边
void addEdge(int u, int v) {
adjMatrix[u][v] = 1;
adjMatrix[v][u] = 1; // 由于是无向图,所以是对称的
}
// 打印邻接矩阵
void printAdjMatrix() {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++)
cout << adjMatrix[i][j] << " ";
cout << endl;
}
}
};
int main() {
// 创建有 4 个顶点的图
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 3);
// 0 1 1 0
// 1 0 1 0
// 1 1 0 1
// 0 0 1 0
g.printAdjMatrix();
return 0;
}
这两个的区别:【根本原因就是一个是链表一个是数组】
- 构造方法
- 添加边【push_back和[] []=1】
虽然邻接矩阵和邻接表都可以使用 vector<vector<int>> 进行定义,这是因为它们本质上都是存储整数的二维结构,但它们表示图的方式和含义完全不同,导致了两种不同的数据结构——vector的强大!!!
3. DFS & BFS
邻接表
// 邻接表:每个顶点的所有邻接顶点都紧凑地存储在链表中,因此你可以直接迭代链表来访问所有邻接点。
// DFS 使用**递归或栈**来实现,从一个起始顶点开始,然后沿着一条路径尽可能深入地访问顶点,直到没有未访问的邻接顶点为止,然后回溯到上一个顶点,继续探索其他路径。
void Graph::DFSUtil(int v, vector<bool>& visited) {
// 标记当前节点为已访问
visited[v] = true;
cout << v << " ";
// 递归遍历所有没有访问过的邻居
// 就是找到这个节点,往后继续递归遍历,相当于遍历adj[v][i]
for (int neighbor : adj[v]) {
if (!visited[neighbor])
DFSUtil(neighbor, visited);
}
}
void Graph::DFS(int v) {
// 初始化所有顶点为未访问
vector<bool> visited(V, false);
DFSUtil(v, visited); // 从v开始遍历
}
// BFS 使用队列来实现,遵循先访问邻近顶点的原则。
// 先访问一个点【出队】,把这个点所有的子节点访问完了【入队再出队】再去访问下一个节点的子节点
void Graph::BFS(int s) {
// 初始化所有顶点为未访问
vector<bool> visited(V, false);
// 创建一个队列用于BFS
queue<int> queue;
// 标记当前节点为已访问并入队
visited[s] = true;
queue.push(s);
// 队列为空时说明所有点都访问完了【连通图】
while(!queue.empty()) {
// 出队一个顶点并打印
s = queue.front();
cout << s << " ";
queue.pop();
// 获取所有邻接顶点。如果一个邻接没被访问过,则标记它并入队
for (int neighbor : adj[s]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
}
}
}
邻接矩阵
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
class GraphMatrix {
int V;
vector<vector<int>> adjMatrix;
public:
GraphMatrix(int V) : V(V), adjMatrix(V, vector<int>(V, 0)) {}
void addEdge(int u, int v) {
adjMatrix[u][v] = 1;
adjMatrix[v][u] = 1;
}
// 每次你想要找到一个顶点的邻接点时,你都需要遍历整个顶点的邻接矩阵行。
// DFS
void DFSUtil(int v, vector<bool>& visited) {
visited[v] = true;
cout << v << " ";
for(int i = 0; i < V; i++) {
// 这里相比与邻接表就多了个adjMatrix[v][i],再矩阵里面我们必须先判断这两个点是否相连
if(adjMatrix[v][i] && !visited[i]) {
DFSUtil(i, visited);
}
}
}
// 这里和邻接表一样
void DFS(int v) {
vector<bool> visited(V, false);
DFSUtil(v, visited);
}
// BFS
void BFS(int s) {
// 初始化未访问
vector<bool> visited(V, false);
queue<int> q;
// 标记当前节点已访问并入队
visited[s] = true;
q.push(s);
// 队列为空时说明所有点都访问完了
while(!q.empty()) {
s = q.front();
cout << s << " ";
q.pop();
// 这里和邻接表不一样,必须遍历整个矩阵
for(int i = 0; i < V; i++) {
if(adjMatrix[s][i] && !visited[i]) {
visited[i] = true;
q.push(i);
}
}
}
}
};
邻接表和邻接矩阵BFS对比
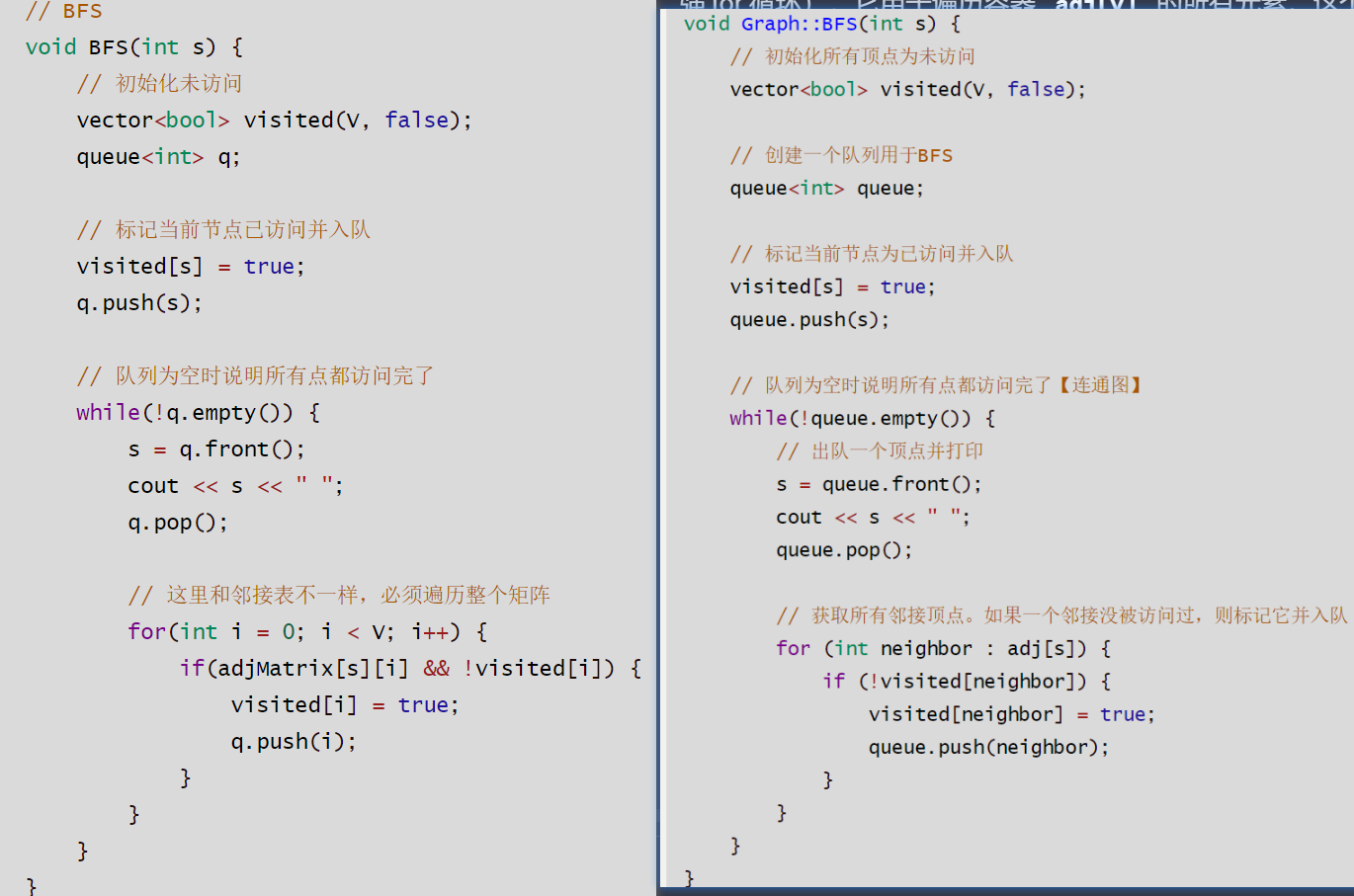
DFS对比
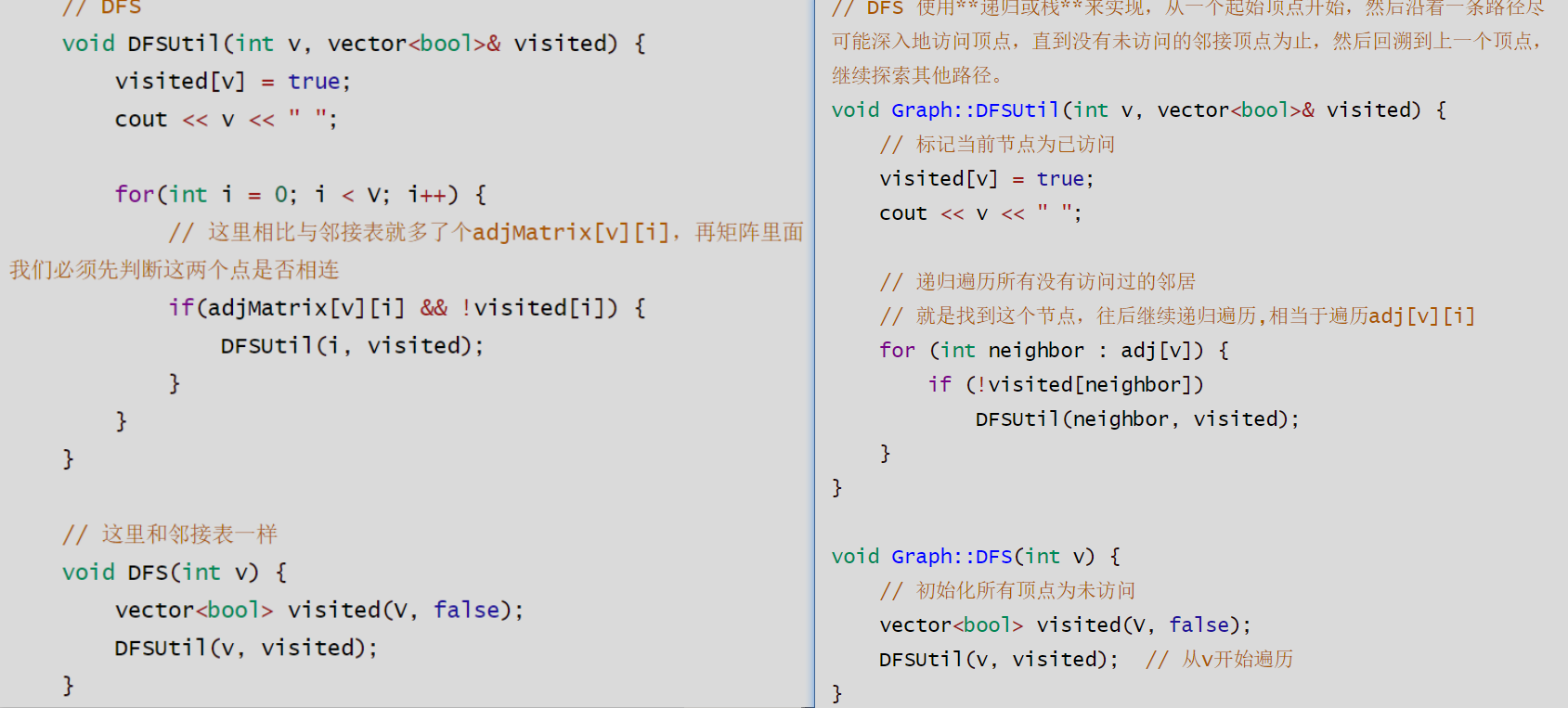
非连通图遍历
非连通图的遍历是遍历图的每个连通分量。对于非连通图,可以使用 DFS 或 BFS 遍历每个连通分量。
邻接表为案例,定义见2.1
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
class Graph {
int V; // 顶点的数量
// vector<vector<int>>看成一个二维向量就行
vector<vector<int>> adj; // 邻接表
public:
Graph(int V); // 构造函数
void addEdge(int v, int w); // 添加边
void printGraph(); // 打印图
void DFSUtil(int v, vector<bool>& visited);
void DFS();
void BFS();
};
Graph::Graph(int V) {
this->V = V;
//resize改变容器大小
adj.resize(V);
}
void Graph::addEdge(int v, int w) {
adj[v].push_back(w); // 添加一个边从v到w
adj[w].push_back(v); // 由于是无向图,也添加一个边从w到v
}
void Graph::printGraph() {
for (int v = 0; v < V; ++v) {
cout << "顶点" << v << "指向 ";
// for增强,会依次取得 adj[v] 的每个元素。
for (int x : adj[v])
cout << "-> " << x;
printf("\n");
}
}
// 非连通图的DFS遍历
void Graph::DFSUtil(int v, vector<bool>& visited) {
// 标记当前节点为已访问
visited[v] = true;
cout << v << " ";
// 递归遍历所有没有访问过的邻居
for (int neighbor : adj[v]) {
if (!visited[neighbor])
DFSUtil(neighbor, visited);
}
}
void Graph::DFS() {
vector<bool> visited(V, false); // 记录访问状态
// 【和连通图的区别,外面要多加一个for和if确保是遍历到了每个点】对每个顶点做DFS,未访问的顶点开始新的DFS
for (int v = 0; v < V; v++) {
if (!visited[v]) {
DFSUtil(v, visited);
}
}
}
// BFS
void Graph::BFS() {
vector<bool> visited(V, false); // 记录访问状态
// 【和连通图的区别,外面要多加一个for和if确保是遍历到了每个点】对每个顶点做BFS
for (int s = 0; s < V; s++) {
if (!visited[s]) {
// 进行一次BFS
queue<int> queue;
visited[s] = true;
queue.push(s);
while(!queue.empty()) {
int s = queue.front();
cout << s << " ";
queue.pop();
for (int neighbor : adj[s])
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
}
}
}
}
int main() {
Graph g(8); // 创建一个包含8个顶点的非连通图
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(3, 4);
g.addEdge(5, 6);
g.addEdge(6, 7);
cout << "DFS Traversal of the Disconnected Graph:" << endl;
g.DFS();
cout<<endl;
cout << "BFS Traversal of the Disconnected Graph:" << endl;
g.BFS();
return 0;
}
画出无向图序列
0 -- 1
| |
3 -- 2
邻接矩阵表示:
0 1 2 3
0 0 1 0 1
1 1 0 1 0
2 0 1 0 1
3 1 0 1 0
邻接表表示:
Vertex 0: 1 3
Vertex 1: 0 2
Vertex 2: 1 3
Vertex 3: 0 2
DFS Sequence: 0 1 2 3
BFS Sequence: 0 1 3 2
4. 最小生成树
Prim 算法【点】
Prim 算法从任意顶点开始,每次添加与当前生成树距离最短的边。
算法步骤:
- 初始化一个空的树结构(最初只包含一个顶点)和一个优先队列(最小堆),用于存放与已选择顶点相连的边。
- 将初始顶点的所有邻边加入优先队列中。
- 当优先队列不为空时,重复以下步骤:
- 从优先队列中取出权重最小的边。
- 如果这条边连接的顶点已经在树中,则忽略它;否则,将该边和顶点添加到树中,并将新加入顶点的所有邻边加入优先队列。
- 当所有顶点都被添加到树中后,算法结束。
算法特点:
- 适用于密集图:在顶点数量较多的情况下效率较高。
- 贪心算法:每一步都选择当前可选边中最小的边。
- 简单易实现:尤其适用于使用邻接矩阵表示的图。
【白话解释版:就是先找到一个点,从这个点开始找到权值最小的一条边进行连接
把这两个点看成一个整体,再找权值最小的边,直到所有点都被连接
注意在这个过程中不能形成环】
#include <iostream>
#include <vector>
#include <climits> // 包含INT_MAX
using namespace std;
class Graph {
int V; // 顶点数量
vector<vector<int>> graph; // 邻接矩阵表示的图
vector<int> parent; // 存储最小生成树
vector<int> key; // 用于存储键值
vector<bool> mstSet; // 代表顶点是否已经在MST中
public:
Graph(int V); // 构造函数
void addEdge(int u, int v, int w); // 添加边
void primMST(); // 计算MST
int minKey(); // 返回不在MST集合中的最小键值的索引
void printMST(); // 打印MST
};
Graph::Graph(int V) {
this->V = V;
graph = vector<vector<int>>(V, vector<int>(V, 0));
parent = vector<int>(V);
key = vector<int>(V, INT_MAX);
mstSet = vector<bool>(V, false);
}
// 添加边到图
void Graph::addEdge(int u, int v, int w) {
graph[u][v] = w;
graph[v][u] = w; // 由于是无向图
}
// 返回不在MST集合中的最小键值的索引
int Graph::minKey() {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// 打印构造的MST
void Graph::printMST() {
cout << "Edge \tWeight\n";
for (int i = 1; i < V; i++)
cout << parent[i] << " - " << i << " \t" << graph[i][parent[i]] << " \n";
}
// 构造并打印MST
void Graph::primMST() {
key[0] = 0; // 使得第一个顶点被选为第一个顶点
parent[0] = -1; // 第一个顶点总是MST的根节点
// MST将有V个顶点
for (int count = 0; count < V - 1; count++) {
int u = minKey(); // 选择最小键值的顶点
mstSet[u] = true; // 添加到MST集合
// 更新邻接顶点的键值和父节点索引
for (int v = 0; v < V; v++) {
// 更新键值只有在以下条件满足时:graph[u][v]不为0;
// v不在mstSet中;graph[u][v]的权重小于key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
printMST(); // 打印构造的MST
}
int main() {
/* 创建以下的图的邻接矩阵
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
Graph g(5);
g.addEdge(0, 1, 2);
g.addEdge(0, 3, 6);
g.addEdge(1, 2, 3);
g.addEdge(1, 3, 8);
g.addEdge(1, 4, 5);
g.addEdge(2, 4, 7);
g.addEdge(3, 4, 9);
// 打印构造的最小生成树
g.primMST();
return 0;
}
克鲁斯卡尔算法【边】
克鲁斯卡尔算法从边的角度出发,选择最小权重的边,同时保证不形成环,直到构成一个最小生成树。
算法步骤
- 初始化:将图中的所有边按权重排序。
- 创建集合:为每个顶点创建一个集合,用于判断是否形成环。
- 选择边:从权重最小的边开始,依次考虑每条边:
- 如果当前边连接的两个顶点属于不同的集合,则选择这条边,并合并两个集合(即加入当前边不会形成环)。
- 如果当前边连接的两个顶点属于同一集合,则忽略这条边(即加入当前边会形成环)。
- 重复上述步骤,直到选择了
V-1条边,其中V是图中顶点的数量。
特点
- 适用于边比较稀疏的图:在边数相对较少的情况下效率较高。
- 边为主导:算法的主要操作是对边进行排序和选择。
- 不依赖起始顶点:与 Prim 算法不同,克鲁斯卡尔算法不从特定的顶点开始。
【白话解释版:先把所有边的权值从小到大排好
依次进行连接,直到所有的点都被连接
同样注意在这个过程中不能形成环】
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 边的结构体,包含起点,终点和权重
struct Edge {
int src, dest, weight;
};
// 图的结构体,包含顶点个数、边的集合
struct Graph {
int V, E;
vector<Edge> edges;
// 添加边到图中
void addEdge(int src, int dest, int weight) {
Edge edge = {src, dest, weight};
edges.push_back(edge);
}
};
// 并查集用来检查是否形成环
struct DisjointSets {
int *parent, *rank;
int n;
DisjointSets(int n) {
this->n = n;
parent = new int[n+1];
rank = new int[n+1];
// 初始化并查集,每个顶点自成一个集合
for (int i = 0; i <= n; i++) {
rank[i] = 0;
parent[i] = i;
}
}
// 查找顶点所在集合的代表
int find(int u) {
if (u != parent[u])
parent[u] = find(parent[u]);
return parent[u];
}
// 合并两个集合
void merge(int x, int y) {
x = find(x), y = find(y);
if (rank[x] > rank[y])
parent[y] = x;
else
parent[x] = y;
if (rank[x] == rank[y])
rank[y]++;
}
};
// 比较两条边权重的函数
bool myComp(const Edge& a, const Edge& b) {
return a.weight < b.weight;
}
// 克鲁斯卡尔算法的实现
void KruskalMST(Graph& graph) {
int V = graph.V;
vector<Edge> result; // 存储最终的最小生成树
int e = 0; // 结果中边的索引
// 按边权重排序
sort(graph.edges.begin(), graph.edges.end(), myComp);
DisjointSets ds(V);
// 遍历所有的边,按权重从小到大
for (auto it = graph.edges.begin(); e < V - 1 && it != graph.edges.end(); ++it) {
int u = it->src;
int v = it->dest;
int set_u = ds.find(u);
int set_v = ds.find(v);
// 如果当前边不构成环
if (set_u != set_v) {
// 添加到结果中
result.push_back(*it);
e++;
ds.merge(set_u, set_v);
}
}
// 打印构建的最小生成树
for (auto it = result.begin(); it != result.end(); ++it)
cout << it->src << " - " << it->dest << " : " << it->weight << endl;
}
int main() {
int V = 4; // 顶点数目
int E = 5; // 边数目
Graph graph = {V, E};
// 添加边:src, dest, weight
graph.addEdge(0, 1, 10);
graph.addEdge(0, 2, 6);
graph.addEdge(0, 3, 5);
graph.addEdge(1, 3, 15);
graph.addEdge(2, 3, 4);
KruskalMST(graph);
return 0;
}
5. 拓扑排序
拓扑排序是对有向无环图(DAG)的所有顶点的线性排序,使得对于每条有向边 uv,顶点 u 在顶点 v 之前。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
class Graph {
int V; // 顶点数目
vector<vector<int>> adj; // 邻接表
public:
Graph(int V); // 构造函数
void addEdge(int v, int w); // 添加边
void topologicalSort(); // 执行拓扑排序
};
Graph::Graph(int V) {
this->V = V;
adj.resize(V);
}
void Graph::addEdge(int v, int w) {
adj[v].push_back(w); // 添加v到w的边
}
//【正式开始】
void Graph::topologicalSort() {
vector<int> in_degree(V, 0);
// 初始化所有顶点的入度
for (int u = 0; u < V; u++)
for (int &v : adj[u])
in_degree[v]++;
queue<int> q;
// 将所有入度为0的顶点加入队列
for (int i = 0; i < V; i++)
if (in_degree[i] == 0)
q.push(i);
int cnt = 0; // 计数,记录当前已输出的顶点数
vector<int> top_order; // 用于存储拓扑排序的结果
while (!q.empty()) {
int u = q.front();
q.pop();
top_order.push_back(u);
// 减少所有相邻顶点的入度
for (int &v : adj[u])
if (--in_degree[v] == 0)
q.push(v);
cnt++;
}
// 检查是否有环【通过访问点是否和图的顶点一致检查】
if (cnt != V) {
cout << "There exists a cycle in the graph\n";
return;
}
// 打印拓扑排序的结果
for (int &x : top_order)
cout << x << " ";
}
int main() {
// 创建图
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Topological Sort of the given graph \n";
g.topologicalSort();
return 0;
}
6. 最短路径
最短路径问题是找出图中两个顶点之间的最短路径。这里是两种常见的最短路径算法的设计思路:
- Dijkstra 算法:适用于加权图中的单源最短路径问题。算法思路是不断选择未访问的最近顶点,并更新其邻居的最短路径。
#include <iostream>
#include <vector>
#include <limits>
using namespace std;
class Graph {
public:
int V; // 顶点数
vector<vector<int>> adj; // 邻接矩阵
Graph(int vertices) : V(vertices) {
adj.resize(V, vector<int>(V, 0));
}
// 添加有向边
void addEdge(int u, int v, int weight) {
adj[u][v] = weight;
}
// Dijkstra算法求单源最短路径
void dijkstra(int src) {
vector<int> dist(V, numeric_limits<int>::max());
vector<bool> visited(V, false);
dist[src] = 0;
for (int count = 0; count < V - 1; count++) {
int u = minDistance(dist, visited);
visited[u] = true;
for (int v = 0; v < V; v++)
if (!visited[v] && adj[u][v] && dist[u] != numeric_limits<int>::max() && dist[u] + adj[u][v] < dist[v])
dist[v] = dist[u] + adj[u][v];
}
// 输出最短路径
cout << "Vertex \t Distance from Source" << endl;
for (int i = 0; i < V; i++)
cout << i << " \t " << dist[i] << endl;
}
// 寻找距离最小的未访问节点
int minDistance(const vector<int>& dist, const vector<bool>& visited) {
int minDist = numeric_limits<int>::max();
int minIndex = -1;
for (int v = 0; v < V; v++)
if (!visited[v] && dist[v] <= minDist)
minDist = dist[v];
minIndex = v;
return minIndex;
}
};
int main() {
int V = 5; // 顶点数
Graph g(V);
g.addEdge(0, 1, 2);
g.addEdge(0, 2, 4);
g.addEdge(1, 2, 1);
g.addEdge(1, 3, 7);
g.addEdge(2, 4, 3);
g.addEdge(3, 4, 1);
g.dijkstra(0);
return 0;
}
- Floyd-Warshall 算法:用于计算图中所有顶点对之间的最短路径。它使用动态规划的方法,考虑每个顶点作为中间顶点的情况。
#include <iostream>
#include <vector>
#include <limits>
using namespace std;
class Graph {
public:
int V; // 顶点数
vector<vector<int>> adj; // 邻接矩阵
Graph(int vertices) : V(vertices) {
adj.resize(V, vector<int>(V, numeric_limits<int>::max())); // 初始化为无穷大
for (int i = 0; i < V; i++)
adj[i][i] = 0; // 对角线上的元素初始化为0
}
// 添加有向边
void addEdge(int u, int v, int weight) {
adj[u][v] = weight;
}
// Floyd-Warshall算法求所有节点对之间的最短路径
void floydWarshall() {
vector<vector<int>> dist = adj;
for (int k = 0; k < V; k++)
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
if (dist[i][k] != numeric_limits<int>::max() && dist[k][j] != numeric_limits<int>::max() && dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
// 输出最短路径
cout << "Shortest Path Matrix:" << endl;
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
if (dist[i][j] == numeric_limits<int>::max())
cout << "INF ";
else
cout << dist[i][j] << " ";
cout << endl;
}
};
int main() {
int V = 5; // 顶点数
Graph g(V);
g.addEdge(0, 1, 2);
g.addEdge(0, 2, 4);
g.addEdge(1, 2, 1);
g.addEdge(1, 3, 7);
g.addEdge(2, 4, 3);
g.addEdge(3, 4, 1);
g.floydWarshall();
return 0;
}
22年期末试卷
应用解答题
1. 最大堆
现有如下的单词,int break else switch double case char float for do ifwhile 请以这些单词构造一棵最大堆 (大根堆)。
#include <iostream>
#include <algorithm>
#include <iterator>
using namespace std;
// 初始堆的时候是自下而上的,因为是从最后一个非叶子节点开始向上构建最大堆
// 但是当发现元素要进行堆调整的时候又是自上而下的,因为要对相关的子节点重新进行排序 —— largest
// 用于调整堆的函数
void heapify(string arr[], int n, int i) {
int largest = i; // 初始化最大元素为根
int l = 2 * i + 1; // 左子节点
int r = 2 * i + 2; // 右子节点
// 找到左右子节点中的max
// 左子节点存在且值>max ->更新max下标【smallest的话把这两个>改成<就行】
if (l < n && arr[l] > arr[largest])
largest = l;
// 同样比较右子节点
if (r < n && arr[r] > arr[largest])
largest = r;
// 如果最大元素不是根节点,将其与根节点交换 -> 保证每个子树的顶部都是该子树的最大值
if (largest != i) {
swap(arr[i], arr[largest]);
// 递归地调整受影响的子树【从之前的largest位置开始调整,因为只影响到了largest这个节点】
heapify(arr, n, largest);
}
}
// 构建最大堆的函数
void buildMaxHeap(string arr[], int n) {
// 从最后一个非叶子节点开始,向上构建最大堆
// 因为叶子节点没什么好排的,堆排序是父、子节点排序
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
}
int main() {
// 定义单词数组
string words[] = {
"int", "break", "else", "switch", "double",
"case", "char", "float", "for", "do", "if", "while"
};
int n = sizeof(words) / sizeof(words[0]);
// 构建最大堆
buildMaxHeap(words, n);
// 输出最大堆
cout << "The max heap is: \n";
for(int i = 0; i < n; ++i) {
cout << words[i] << ' ';
}
return 0;
}
2. 散列函数
现有如下的单词,int struct break else switch double case enum charreturn union const float continue for void default do if while static请以这些单词构造使用拉链法解决冲突的散列表,并计算查找成功时的平均查找长度(ASL)。 (根据需要自定义散列函数)
#include <iostream>
#include <list>
#include <string>
using namespace std;
// 定义散列表的大小
const int TABLE_SIZE = 10;
// 散列函数 -- 除留余数法
// 计算并返回散列值,也就是HashTable的index
int hashFunction(const string &key) {
return key.length() % TABLE_SIZE; // 使用字符串长度模散列表大小作为散列值
}
// 计算ASL
double calculateASL(list<string> table[],int n) {
int totalElements = 0; // 整个散列表的元素总数
double totalComparisons = 0; // 所有元素的总比较次数,这里设为double因为后面要求平均数可能会有小数
cout <<"桶:元素数量 累计比较次数"<< endl;
// 遍历每个桶
for (int i = 0; i < TABLE_SIZE; ++i) {
int listSize = table[i].size();// 获取第i个槽位的链表长度,即元素数量
// totalElements += listSize; // 累加总元素数
// 计算桶内所有元素的比较次数,使用等差数列求和公式n*(n+1)/2
// 考虑链表中的每个位置,第1个位置找到的概率是1/n,需要1次比较;第2个位置是1/n,需要2次比较;
// 依此类推,直到第n个位置,需要n次比较。所以总的比较次数是1 + 2 + 3 + ... + n
totalComparisons += listSize * (listSize + 1) / 2;
// 计算并返回ASL,即总比较次数除以总元素数
cout << i <<": " << listSize <<" "<< totalComparisons<< endl;
}
return totalElements == 0 ? 0 :totalComparisons / n;
}
int main() {
string words[] = {
"int", "struct", "break", "else", "switch", "double", "case", "enum",
"char", "return", "union", "const", "float", "continue", "for", "void",
"default", "do", "if", "while", "static"
};
int n = sizeof(words) / sizeof(words[0]); // 单词总数
// 创建散列表,每个槽位是一个链表 --> 拉链法
list<string> hashTable[TABLE_SIZE];
// 插入单词到散列表
for (int i = 0; i < n; ++i) {
int index = hashFunction(words[i]); // 计算每个单词的散列值
hashTable[index].push_back(words[i]); // 添加到对应散列值的桶的链表末尾,这里就是拉链法了
}
// 计算并输出ASL
double asl = calculateASL(hashTable,n);
cout << "平均查找长度(ASL)是: " << asl << endl;
return 0;
}
3. 画出最小生成树
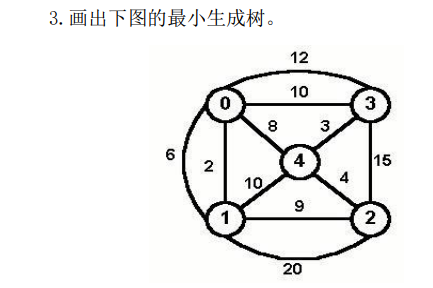
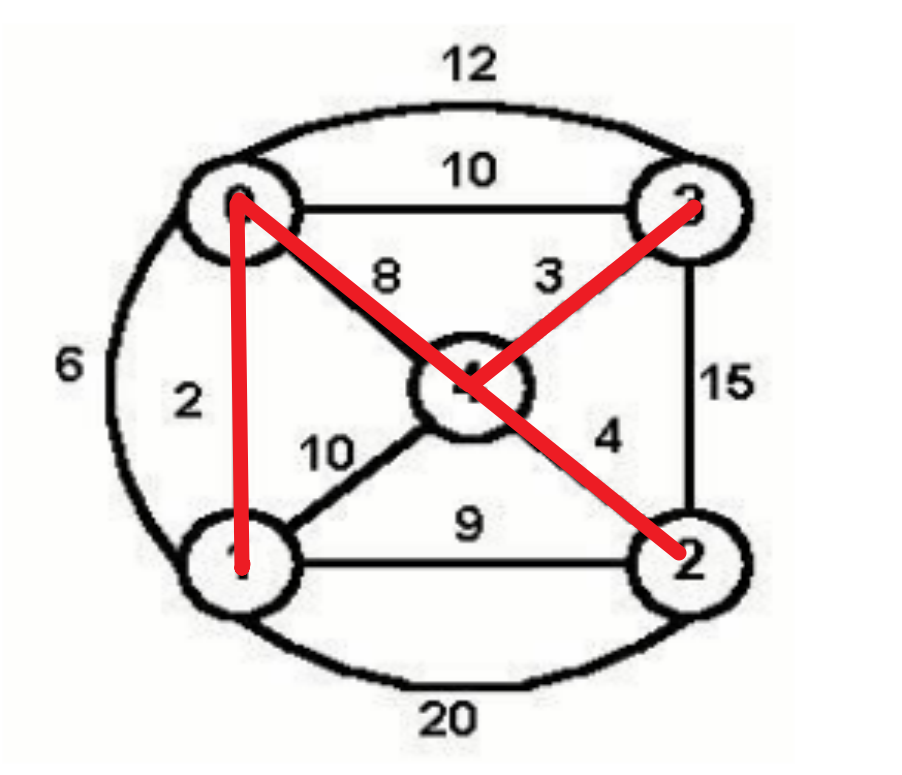
4. 满k叉树性质

(1) 编号 = k * n + i
0
/ \
1 2
/ \ / \
3 4 5 6
-
如果从0开始节点编号
- 左节点是k*h+1
- 右节点是k*h+2
-
对于节点 1的第 1 个子节点是 3:2 * 1 + 1 = 3。
-
对于节点 2的第 2 个子节点是 6:2 * 2 + 2 = 6。
(2) 在满k叉树中,一个节点有右兄弟的条件是它不是其父节点的最后一个子节点,即n % k != 0
继续使用上面的二叉树例子:
- 节点 3(编号为 3)的计算方法是:3 % 2 != 0,所以它有右兄弟(节点 4)。
- 节点 4(编号为 4)的计算方法是:4% 2 = 0,所以它没有右兄弟。
(3) 深度为 h 的满 k 叉树的节点总数 n 可以通过求解等比数列的和来得到:n = 1 + k + k^2 + k^3 + … + k^(h-1)
通过等比数列的和公式推导出来:h = logk(n * (k-1) + 1)
或者写成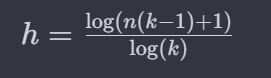
继续使用上面的二叉树例子:
- 深度 h = 3,节点总数 n 计算为:1 + 2 + 2^2 = 7。
- 如果我们知道 n = 7,那么深度 h 的计算方法是:h = log2(7*(2-1) + 1) = 3。
算法设计题
1. 二叉排序树的插入
请设计递归算法以实现二叉排序树的插入操作。(注意: 需要先写出二又排序树的存储结构)
思路:就是简单的递归啦
注意点:
- 插入的判断条件:小于左节点/大于右节点
- 插入最后要返回更新后的树根
- 注意是struct
// 递归实现二叉排序树
#include<iostream>
using namespace std;
struct TreeNode {
int data;
TreeNode *left,*right;
// 构造函数 --NULL和nullptr有什么区别?
TreeNode(int x):data(x),left(nullptr),right(nullptr){}
};
// 插入
TreeNode* insert (TreeNode*root, int x){
if(!root) return new TreeNode(x);
// 注意这个判断条件,,,这里将新节点链接到树上
if(x < root->data) root->left = insert(root->left,x);
if(x > root->data) root->right = insert(root->right,x);
// 为什么这里还要?--返回更新后的树根
return root;
}
//前序
void inorder(TreeNode* root){
if(!root) return ;
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
int main(){
TreeNode* root = nullptr;
// 插入元素
root = insert(root, 8);
root = insert(root, 3);
root = insert(root, 10);
inorder(root);
cout<<endl;
root = insert(root, 1);
root = insert(root, 6);
inorder(root);
return 0;
}
2.哈夫曼树编码
请写算法:把哈夫曼树的叶子结点以编码从长到短的顺序输出。(注意: 需要先写出哈夫曼树的存储结构)
#include <iostream>
#include <string>
using namespace std;
// 定义霍夫曼树的节点结构
struct HuffmanNode {
char data; // 节点代表的字符
int freq; // 字符出现的频率
HuffmanNode *left, *right; // 指向左右子节点的指针
// 我趣构造函数都忘记写了
HuffmanNode(char data, int freq):data(data),freq(freq),left(nullptr),right(nullptr) {}
};
// 找出频率最小的两个节点
// first--最小节点指针;second--次节点指针
void findTwoMinimum(HuffmanNode* array[], int size, HuffmanNode** first, HuffmanNode** second) {
// 要记录索引,因为后面还要将找到的最小点移除
// 但是这里的移除并不是真正的删除,而是置为NULL
int idxFirst = -1;
int idxSecond = -1;
*first = *second = NULL;
for (int i = 0; i < size; ++i) {
// 当前节点非空(即还没有被选为最小或次小节点):
if (array[i]) {
// 还没有找到最小节点,或者当前节点的频率 < 已知的最小节点频率,那么更新最小节点及其索引。
if (*first == NULL || array[i]->freq < (*first)->freq) {
// 在更新最小节点之前,先把 frist 赋值给 second
*second = *first;
*first = array[i];
idxSecond = idxFirst;
idxFirst = i;
// 更新 second
} else if (*second == NULL || array[i]->freq < (*second)->freq) {
*second = array[i];
idxSecond = i;
}
}
}
// 将找到的最小节点从数组中移除,以避免重复选择
// 所以前面为什么要 idxFirst 和 idxSecond
if (idxFirst >= 0) array[idxFirst] = NULL;
if (idxSecond >= 0) array[idxSecond] = NULL;
}
// 构建哈夫曼树的正式函数
// 想想参数,我们好像只有data和freq的数组
// 还需要一个size,因为要创建HaffmanTree数组
HuffmanNode* buildHuffmanTree(char data[], int freq[], int size) {
HuffmanNode *left, *right, *top;
HuffmanNode* array[size]; // 用于存放节点的数组
// 这个哈夫曼树节点包括元素、频率、左右子节点
// 前面的size部分存的是原始数据,后面存的就是构造的树了
// 因为包括左右子节点,所以array节点顺序!= 哈夫曼树节点顺序
// 初始化节点
for (int i = 0; i < size; ++i)
array[i] = new HuffmanNode(data[i], freq[i]);
// 构建树的循环
while (true) {
int count = 0;
// 用于计数非空节点
// 在构建霍夫曼树的过程中,需要不断地将频率最低的两个节点合并为一个新的节点,并从数组中移除这两个最低频率的节点,然后将新节点加回数组。
// 随着这个过程的进行,数组中会有越来越多的NULL值,表示那些位置的原始节点已经被合并并移除了。
// count变量用于在每次循环时计数数组中还有多少非空(array[i]不是NULL)的节点。
// 当count变为1时,意味着所有的节点已经被合并成一颗单独的树,这时构建过程完成,循环结束。
for (int i = 0; i < size; i++)
if (array[i]) count++;
if (count == 1) break; // 当只剩一个节点时退出循环
// 1.找到频率最小的两个节点 --同时在array中删掉了原来的两个节点
// 这里要什么参数?
// 首先肯定要array,那你找最小的两个节点肯定是先要给两个节点进去left、right【这两个节点要新建】
// 因为我们要在array里面找最小的两个,那size肯定也要,和后面新建的节点进行区分
findTwoMinimum(array, size, &left, &right);
// 2.创建一个新父节点,并把左右子节点设置为最小节点和次小节点
// $ 用作占位符或标记,表示该节点是一个内部节点,后面print会去掉的
top = new HuffmanNode('$', left->freq + right->freq);
top->left = left;
top->right = right;
// 3.把父节点加进array -- 找到array最近的空位置加入
for (int i = 0; i < size; i++)
// 找到非空的位置存入
if (!array[i]) {
array[i] = top;
break;
}
}
// 查找并返回根节点
// 在霍夫曼树构建过程的最后阶段,你会重复地找出两个最小频率的节点,将它们结合成一个新的节点,
//直到只剩下一个节点。这个最后的节点就是霍夫曼树的根节点
// 也就是说array里面到最后就只有一个节点了,这个节点就是根节点
HuffmanNode* root = NULL;
for (int i = 0; i < size; i++)
if (array[i]) {
root = array[i];
break;
}
return root;
}
// 打印霍夫曼编码
void printCodes(struct HuffmanNode* root, string str) {
// 解释一下这里的逻辑,首先现在array里面有2种点
// 1是最开始存入的初始值,现在都变成nullprt了
// 2是构建的父节点,值为 $
// 看这个判断条件,!=$也就意味着是访问到原来的节点了,这个时候就可以输出
// 有一个混淆的点是:在打印期间和array就没关系了,不会因为array里面有nullptr就导致树访问不了
// 反正就是一旦树构建完成,只需要根节点的引用就可以访问整个树
if (!root) return; // 如果节点为空,则返回
if (root->data != '$') cout << root->data << ": " << str << "\n"; // 如果是叶节点,打印字符及其霍夫曼编码
printCodes(root->left, str + "0"); // 递归处理左子树
printCodes(root->right, str + "1"); // 递归处理右子树
}
// 主函数
int main() {
// 输入数据和频率
char arr[] = {'a', 'b', 'cpp', 'd', 'e', 'f'};
int freq[] = {5, 9, 12, 13, 16, 45};
int size = sizeof(arr) / sizeof(arr[0]);
// 构建霍夫曼树
HuffmanNode* root = buildHuffmanTree(arr, freq, size);
// 如果根节点不为空,则打印霍夫曼编码
if (root)
printCodes(root, "");
else
cout << "Error constructing Huffman Tree.";
return 0;
}
3. 拓扑排序
假设图以邻接矩阵做存储结构,请写出拓扑排序算法。(注意:需要先写出邻接矩阵的存储结构)
思路:入度为0,删掉该节点,一并把该节点的出度线也删掉
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
void topologicalSort(vector<vector<int>>& matrix) {
int n = matrix.size(); // 图中顶点的数量
vector<int> in_degree(n, 0); // 记录每个顶点的入度
// 1. 计算每个节点的入度
for (int u = 0; u < n; u++)
for (int v = 0; v < n; v++)
if (matrix[u][v]) // 如果u到v有边
in_degree[v]++;
// 2. 依次放进队列q里面
queue<int> q; // 存储所有入度为0的顶点
for (int i = 0; i < n; i++)
if (in_degree[i] == 0)
q.push(i);
int count = 0; // 记录访问过的顶点数量
vector<int> top_order; // 存储拓扑排序的结果
// 3. 遍历队列【拿出:放进sort减入度;放进:存在且减后入度为0】
while (!q.empty()) {
// 从队列拿出元素放到拓扑排序里面
int u = q.front();
q.pop();
top_order.push_back(u); // 添加到拓扑排序的结果中
// 减少所有和u相关的相邻节点的入度
for (int v = 0; v < n; v++)
// 前面代表存在(不为0),后面代表减少入度
if (matrix[u][v] && --in_degree[v] == 0)
q.push(v);
count++;
}
// 检查是否存在环
if (count != n) {
cout << "有环!";
return;
}
// 打印拓扑排序结果
for (int i : top_order)
cout << i << " ";
}
int main() {
// 示例图的邻接矩阵
vector<vector<int>> matrix = {
{0, 1, 1, 0}, // 图中有边0->1, 0->2
{0, 0, 1, 0}, // 图中有边1->2
{0, 0, 0, 1}, // 图中有边2->3
{0, 0, 0, 0} // 顶点3没有出边
};
topologicalSort(matrix);
return 0;
}
综合算法设计题
在某个程序设计语言中,如果其不提供指针以及引用的编程功能给编程人员,编程人员通常会采用数组的方法来模拟单链表的操作,此时构建出来的单链表通常会称为静态单链表。
现在有一个线性表存储在静态单链表 L中,且该单链表的结点是按值非递减有序排列的,试编写一个算法在静态单链表L 中插入值为X的结点,使得L 仍然有序。(注意:需要先写出静态单链表的存储结构,而且可以假设X放入数组的 i 号下标位置)
#include<iostream>
using namespace std;
// 链表的最大长度
const int MAXN = 1000;
// 节点定义
struct Node{
int data;
int next;
}Link[MAXN];
// 链表当前最后一个元素的索引
int lastNodeIndex = 0;
// 插入操作
void insert(int X) {
// 从头开始找
int temp = 0;
// 找到插入位置的前一个位置【判断条件:非首次插入且下一个的值 > x】
while(staticList[temp].next != -1 && staticList[staticList[temp].next].value < X)
temp = staticList[temp].next;
// 进行插入 --现在已经找到要插入的位置了,就是temp下一个处
// 所以我们要干的就是插入(废话
// 首先我们得明白一点,就是这个数组他不一定是按顺序排放的,但是它的next一定是按顺序排放的
// 数组插入要干嘛,先直接在数组最后插入一个新的Node,再改这个Node得data和Next就行,不用还找到Node应该放在数组得具体的具体哪个位置
int newNode = ++lastNodeIndex; // 所以这里要有链表的最后一个元素索引值
Link[newNode].data = x; // 插入值,改data
// 更新链接
// newNode的next为前一个节点的next
Link[newNode].next = Link[temp].next;
// 前一个节点的next变成newNode了
Link[temp].next = newNode;
}
int main(){
// 初始化静态单链表,-1 表示空指针
Link[0].next = -1; // 头节点
insert(10);
insert(20);
insert(15);
insert(6);
insert(11);
// 输出链表
int temp = Link[0].next; // 从头节点开始
while(temp != -1) {
cout << Link[temp].data << " ";
temp = Link[temp].next;
}
return 0;
}
#include<iostream>
using namespace std;
const int MAXN = 1000; // 定义最大顶点数
// 首先理一下拓扑排序的步骤
// 1. 计算每个点的入度
// 1. 找到入度为0的节点
// 2. 把这些节点放进数组,并删掉这些节点的出度
// cal函数过后起码就要这些变量
// 1.记录邻接矩阵的二维数组
int matrix[MAXN][MAXN] = {0};
// 2. 记录入度的一维矩阵(因为数字是索引
int indegree[MAXN] = (0);
// 3. 记录顶点数
int n;
// 4. 排序的数组
int result[MAXN];
//1. 计算每个点的入度
void cal(){
for(int i = 0;i<n;i++)
for(int j=0;j<n;j++)
if(maxtrix[j][i]) indegree[i]++;
}
// 正式进行拓扑排序
void topoSort(){
// 首先进行拓扑排序是有一个队列的思想在里面的,因为你要不断通过删除入度为0的节点影响别的节点
// 但素我们又不想用queue,就用数组实现queue
int order[MAXN]; //模拟队列
int head; // 队头
int tail; // 队尾
int count; //相当于排序数组的索引指针
// 当队列不为空的时候
while(head!=tail){
// 取出一个顶点,把它放进我们排序的数组里面
int current = order[head++];
result[count++] = current;
// 取出的这个节点对其他节点的入度有什么影响呢
for(int i=0;i<n;i++){
if(maxtrix[current][i]) indegree[i]--;
// --后可能出现入度为0的情况
// 那我们就在数组尾部加入这个节点
if(indegree[i]==0) order[tail++]=i;
}
}
// 打印一下结果
for(int i = 0; i < count; ++i)
cout << result[i] << " ";
}
22-23
应用解答题:
- 最大堆【✔】
- 散列函数(拉链法)
- 最小生成树
- 满k叉树的关系【必看】
算法设计题:
- 二叉树的插入操作(递归)
- 哈夫曼树字节点编码顺序
- 拓扑排序(邻接矩阵)
综合算法设计题:
- 静态单列表的插入
17-18
应用解答题:
- 循环队列元素个数计算表达式
- 稀疏矩阵
- 最小堆【✔】
- 快速排序【✔】
- 满k叉树关系
算法设计题:
- 删除二叉树节点
- 哈夫曼树二进制编码
综合算法设计题:
- 图:迷宫最短距离
16-17
应用解答题:
- 循环队列求当前个数
13-14
- 二叉树前序遍历
- 画出二叉搜索树
- 哈夫曼压缩了多少
- 邻接矩阵的DFS和BFS
- 克鲁斯卡尔法
hyl作业
1:线性表的插入(递增有序&非递减有序),循环链表实现找到最小值并删除
2:逆置单链表(不额外产生空间)
3:递归实现单链表的建立、输出、逆置
4:中前后序的创建和输出
5:根据前序遍历判断是否为二叉查找树,二叉查找树的建立、查找、插入、删除
6:邻接矩阵&表,DFS&BFS
7:最小生成树【1】、最短路径、拓扑排序
8:快排&堆排
第八章
- 最短路径
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// 寻找最小距离的顶点,且未被处理
int minDistance(vector<int>& dist, vector<bool>& sptSet, int V) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
// 未被处理 && 小于min
// 注意要存下min和min_index
if (sptSet[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
// 打印构建的距离数组
void printSolution(vector<int>& dist, int V) {
cout << "Vertex \t Distance from Source" << endl;
for (int i = 0; i < V; i++)
cout << i << " \t\t" << dist[i] << endl;
}
// Dijkstra算法的实现
void dijkstra(vector<vector<int>>& graph, int src, int V) {
vector<int> dist(V, INT_MAX); // 存储从源到i的最短距离,初始值都为INT_MAX
vector<bool> sptSet(V, false); // 标记顶点是否已完成
dist[src] = 0; // 源点到自身的距离总是0
// 找出所有顶点的最短路径
for (int count = 0; count < V - 1; count++) {
int u = minDistance(dist, sptSet, V); // 选择最小距离顶点
sptSet[u] = true; // 标记为已处理
// 更新所有相邻顶点的距离
for (int v = 0; v < V; v++)
// 没有被处理 && 值不为0 && 目前存在这么条路 && 路的距离小
if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
printSolution(dist, V);
}
// 测试Dijkstra算法
int main() {
// 示例图的邻接矩阵表示
vector<vector<int>> graph = {
{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}
};
dijkstra(graph, 0, graph.size()); // 以顶点0为源点
return 0;
}
-
初始化:
dist[]:存储从源点到每个顶点的最短路径估计,初始化为INT_MAX,表示一开始认为所有顶点都是不可达的。sptSet[]:一个布尔数组,用来标记每个顶点的最短路径是否已经被找到(或该顶点是否已经被处理)。所有顶点初始标记为false。- 将源点到自身的距离设为0,即
dist[src] = 0。
-
执行算法:
对于图中的每个顶点(顶点数减1次):
-
a. 选择一个最小距离的未处理顶点 u,即 dist[u] 最小且 sptSet[u] == false
-
b. 标记顶点 u 为已处理,即 sptSet[u] = true
-
cpp. 更新所有 u 的未处理邻接顶点 v 的距离。更新的条件是:
-
存在从
u到v的边,即graph[u][v] != 0。 -
顶点
v尚未被处理,即sptSet[v] == false。 -
通过
u到达v的路径比当前已知的dist[v]更短,即dist[u] + graph[u][v] < dist[v]。
-
-
第九章
- 单链表排序
#include<iostream>
using namespace std;
// 链表节点结构体
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
// 直接插入排序
void insertionSortList(ListNode *&head) {
// 创建一个哑节点作为已排序链表的头部
ListNode = new ListNode(0);
ListNode *curr = head; // 当前遍历到的节点
while (curr != NULL) {
// 保存下一个节点
ListNode *next_temp = curr->next;
// 找到当前节点在已排序链表中的位置
ListNode *p = sorted;
while (p->next != NULL && p->next->val < curr->val) {
p = p->next;
}
// 将当前节点插入到已排序链表中
curr->next = p->next;
p->next = curr;
// 移动到原链表中的下一个节点
curr = next_temp;
}
// 更新头结点
head = sorted->next;
delete sorted; // 删除哑节点
}
int main() {
// 示例:创建并初始化链表
ListNode *head = new ListNode(4);
head->next = new ListNode(2);
head->next->next = new ListNode(1);
head->next->next->next = new ListNode(3);
// 执行插入排序
insertionSortList(head);
// 输出排序后的链表
while (head != NULL) {
cout << head->val << " ";
head = head->next;
}
return 0;
}
- 快速排序
#include <iostream>
using namespace std;
// 交换函数
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
/* 该函数取最右侧元素作为基准,将小于基准的元素放在基准左边,
大于基准的元素放在基准右边,最终返回基准元素的正确位置 */
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // pivot
int i = (low - 1); // 标识小于基准元素部分的边界
for (int j = low; j <= high - 1; j++) {
// 现在的元素小于pivot
if (arr[j] < pivot) {
i++; // 下标++
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
// 快速排序函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
// arr[pi] 基准现在放在正确位置
// 也就是分区操作后基准元素所在索引
int pi = partition(arr, low, high);
// 分别对元素进行排序
// 分区前和分区后
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* 辅助函数,打印数组元素 */
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
// 测试快速排序
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
cout << "Sorted array: \n";
printArray(arr, n);
return 0;
}
我再理一下代码的思路
- partition函数主要就是将最后一个元素作为pivot,i作为小于基准元素部分的边界,从左到右遍历数组,如果现在的元素小于pivot,就说明这个元素应该被放在左边,那我们的边界也要对应向右移动一位(这里为什么要swap(i,j)呢),等遍历完所有的元素,i及i左边的元素都小于pivot,这个时候再将pivot和i+1位置的元素互换,就可以得到想要的数组了
- 接下来就是不断对左边和右边分区的不断重复partition函数,直到所有的元素排列成功
- 我明白了,i只是代表小于基准的边界,我们还需要把小于基准的元素放入边界里面,那为什么一定是i和j交换呢?
- 也就是说这个交换的过程,不但把小于基准的元素放到了边界内,还把大于基准的元素放到了边界外





















 468
468











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








