二叉树的顺序存储结构

最新推荐文章于 2024-10-04 23:22:41 发布

7urin9

最新推荐文章于 2024-10-04 23:22:41 发布

阅读量1w

点赞数 3

分类专栏：数据结构文章标签：二叉树存储类 c

本文链接：https://blog.csdn.net/KongkOngL/article/details/38764101

版权

本文介绍如何在顺序存储结构中建立和操作完全二叉树，包括层序输入、遍历、节点修改、插入子树和删除子树等操作。通过示例展示这些操作的具体过程。

摘要由CSDN通过智能技术生成

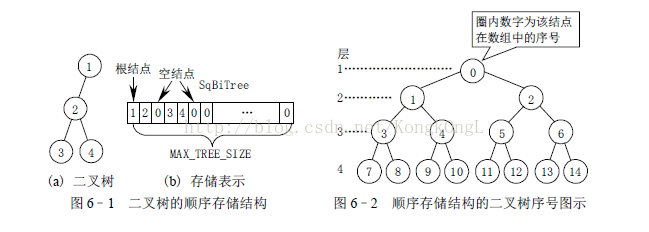
// c6-1.h 二叉树的顺序存储结构(见图6.1)
#define MAX_TREE_SIZE 100 // 二叉树的最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE]; // 0号单元存储根结点
struct position
{
	int level,order; // 结点的层,本层序号(按满二叉树计算)
};

在顺序存储结构中，如图62 所示，第i 层结点的序号从2i1 -1～2i-2；序号为i 的结
点，其双亲序号为(i+1)/2-1，其左右孩子序号分别为2i+1 和2i+2；除了根结点，序号为
奇数的结点是其双亲的左孩子，它的右兄弟的序号是它的序号+1；序号为偶数的结点是其

双亲的右孩子，它的左兄弟的序号是它的序号-1；i 层的满二叉树，其结点总数为2i-1。

显然，在顺序存储结构中，按层序输入二叉树是最方便的。当最后一个结点的值输入
后，输入给定符号表示结束。二叉树的顺序存储结构适合存完全二叉树或近似完全二
叉树。
bo6-1.cpp 是采用顺序存储结构的基本操作程序，main6-1.cpp 是检验这些基本操作的
主程序。为了使这两个程序在结点类型为整型和字符型时都能使用，采用了编译预处理的
“#define”、“#if”等命令。这样，只要将main6-1.cpp 的第2 行或第3 行改为注释行
即可。

// bo6-1.cpp 二叉树的顺序存储(存储结构由c6-1.h定义)的基本操作(23个)
#define ClearBiTree InitBiTree // 在顺序存储结构中，两函数完全一样
#define DestroyBiTree InitBiTree // 在顺序存储结构中，两函数完全一样
void InitBiTree(SqBiTree T)
{ // 构造空二叉树T。因为T是数组名，故不需要&
	int i;
	for(i=0;i<MAX_TREE_SIZE;i++)
		T[i]=Nil; // 初值为空(Nil在主程中定义)
}
void CreateBiTree(SqBiTree T)
{ // 按层序次序输入二叉树中结点的值(字符型或整型), 构造顺序存储的二叉树T
	int i=0;
	InitBiTree(T); // 构造空二叉树T
#if CHAR // 结点类型为字符
	int l;
	char s[MAX_TREE_SIZE];
	cout<<"请按层序输入结点的值(字符)，空格表示空结点，结点数≤"<<MAX_TREE_SIZE<<':'<<endl;
	gets(s); // 输入字符串
	l=strlen(s); // 求字符串的长度
	for(;i<l;i++) // 将字符串赋值给T
		T[i]=s[i];
#else // 结点类型为整型
	cout<<"请按层序输入结点的值(整型)，0表示空结点，输999结束。结点数≤"<<MAX_TREE_SIZE<<':'<<endl;
	while(1)
	{
		cin>>T[i];
		if(T[i]==999)
		{
			T[i]=Nil;
			break;
		}
		i++;
	}
#endif
	for(i=1;i<MAX_TREE_SIZE;i++)
		if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) // 此结点(不空)无双亲且不是根
		{
			cout<<"出现无双亲的非根结点"<<T[i]<<endl;
			exit(ERROR);
		}
}
Status BiTreeEmpty(SqBiTree T)
{ // 初始条件：二叉树T存在。操作结果：若T为空二叉树