Triton矩阵乘以及缓存优化

假设所需要计算的block一共是81，我们试图以第二种计算顺序来计算，因为这样占总缓存的大小小，缓存命中率高。

这里grid=一个标量，所以是一维的。

形如M*N的矩阵，被分解为很多个BLOCK_SIZE_M*BLOCK_SIZE_N的小矩阵，小矩阵的数量为grid  = triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N'])

观察函数内部

pid = tl.program_id(axis=0)，因为grid是一维的，所以这里就是当前块是总块数里的哪一块，可以理解为一共81个block任务，是第几个任务。

我们假设实际A*B=C，

triton.cdiv(574,64) = 8.9向上取整数 = 9

A，B形状是574*574，分小块的形状是64*64，这样一共有9*9 = 81块，pid就是0~80，

这里用574/64=9,所以num_pid_m和num_pid_n都是9

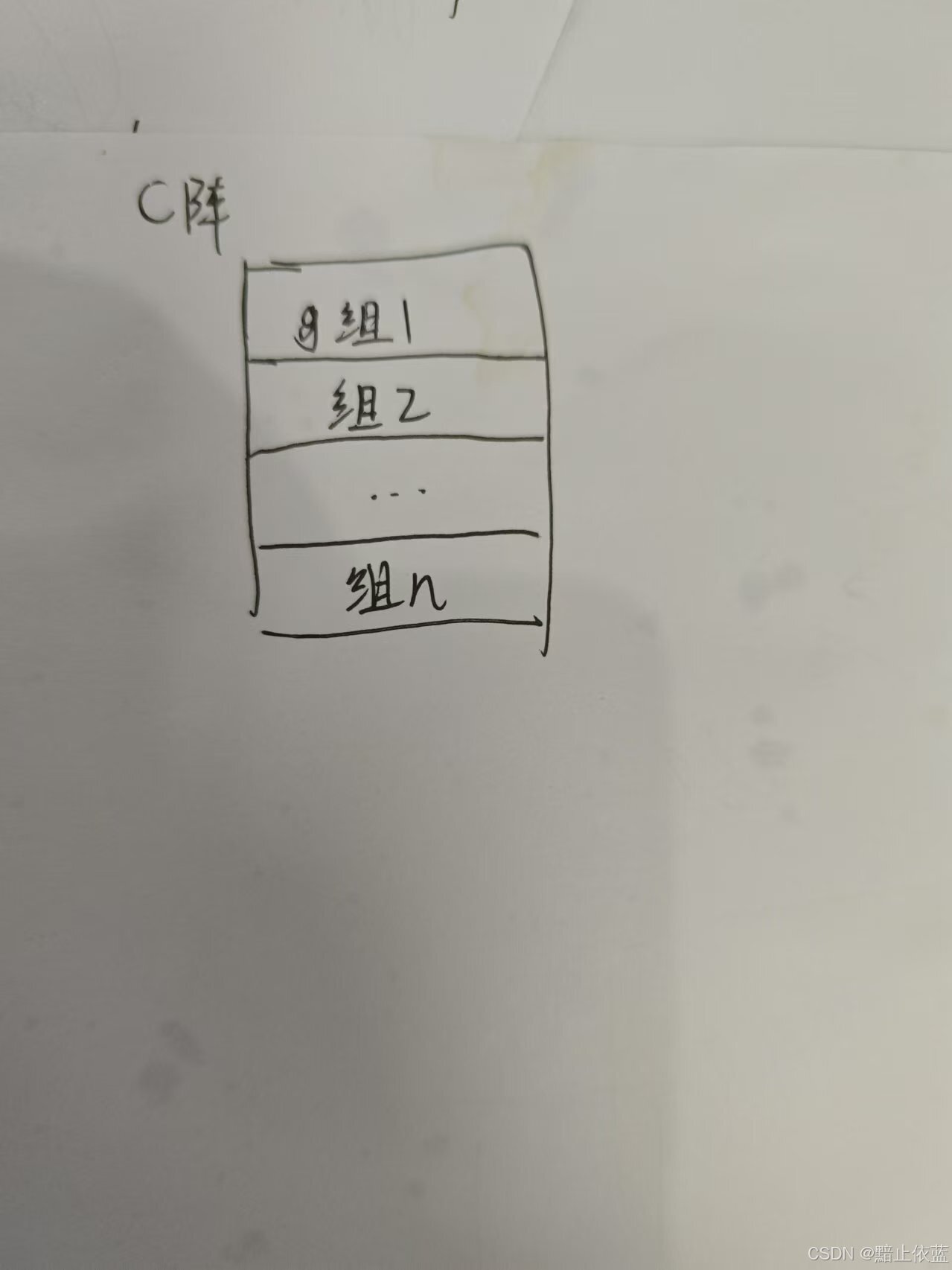
num_pid_in_group = GROUP_SIZE_M * num_pid_n，算的是一个组有多少块，这里假设是3*9，所以一组27块，这里的组应该是人为划定的，因为算一个矩阵c的元素，需要用到a矩阵的一列，和b矩阵的一行，所以分组基于 num_pid_n，然后再选择几行。

group_id = pid // num_pid_in_group算组id，一组27个小块，当前pid//27就得到所在组id，比如30//27=1,说明30块在组1。

first_pid_m = group_id * GROUP_SIZE_M，每一组的第一个块在结果矩阵中是第几行。

因为数据不一定能整除，最后一个组可能少几行。这里group_size_m,算的是当前组一共几行。

group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)

pid_m = first_pid_m + (pid % group_size_m)
    pid_n = (pid % num_pid_in_group) // group_size_m

这两行做映射，是关于pid和结果矩阵中块位置的映射。

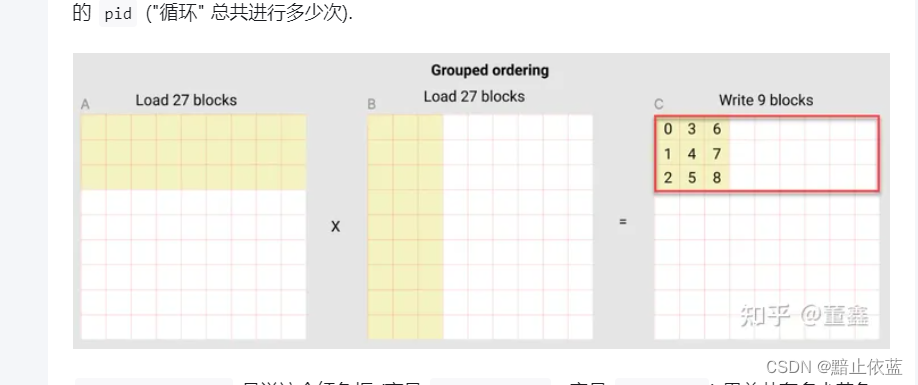
这里官网更新之前的代码是错误的，pid%group_size_m得到的并不是当前所在计算块相对于组的行数。这样在最后一行填不满的情况下计算会错误，实际上的代码应该是

first_pid_m +（pid%num_pid_in_group）%group_size_m

行坐标=当前组第一个块的行位置+pid%每组行数，pid%3知，pid三个三个一排，也就是算的当前pid在当前组里相对是第几行，比如如果是4，4%3=1，可知pid=4在当前组第一行（0，1，2），那么pid%每组行数就可以相对整组位移，最终可以知建立pid和c矩阵中行位置的映射

假设pid = 29，属于 29/27 ->组1，组1的第一个块的行是1*3 = 3，pid%3 = 2 ， 所以可以得到在总的分块里，pid = 29 <----> pid_m = 3+2 = 5。

列坐标=pid%每组总数//每组行数，pid%每组总数可知当前组还剩下几个block，也就是27块中的第几块，比如29%27就会得到2，然后2//3=1就知道在第几列了，

所以pid的对应关系就和上图的一样的顺序对应。

这里比如想要计算块pid=4，那么就需要拿到A的第一行和B的第一列，坐标为(1,1)

这里各自会得到一个二维矩阵，里面的指针值就是所指向的元素位置，这里只是第一块

假设计算结果矩阵中的(1,1)位置的块，

offs_am = (1*64+[0,63])%746 = [64,127]

offs_k = [0,63]

可以想象的要做的事情是生成一个指针矩阵a_ptrs，其中的指针分别指向对应的A小块的数据元素，再次基础上迭代，就可以要计算的C矩阵1，1位置的block，

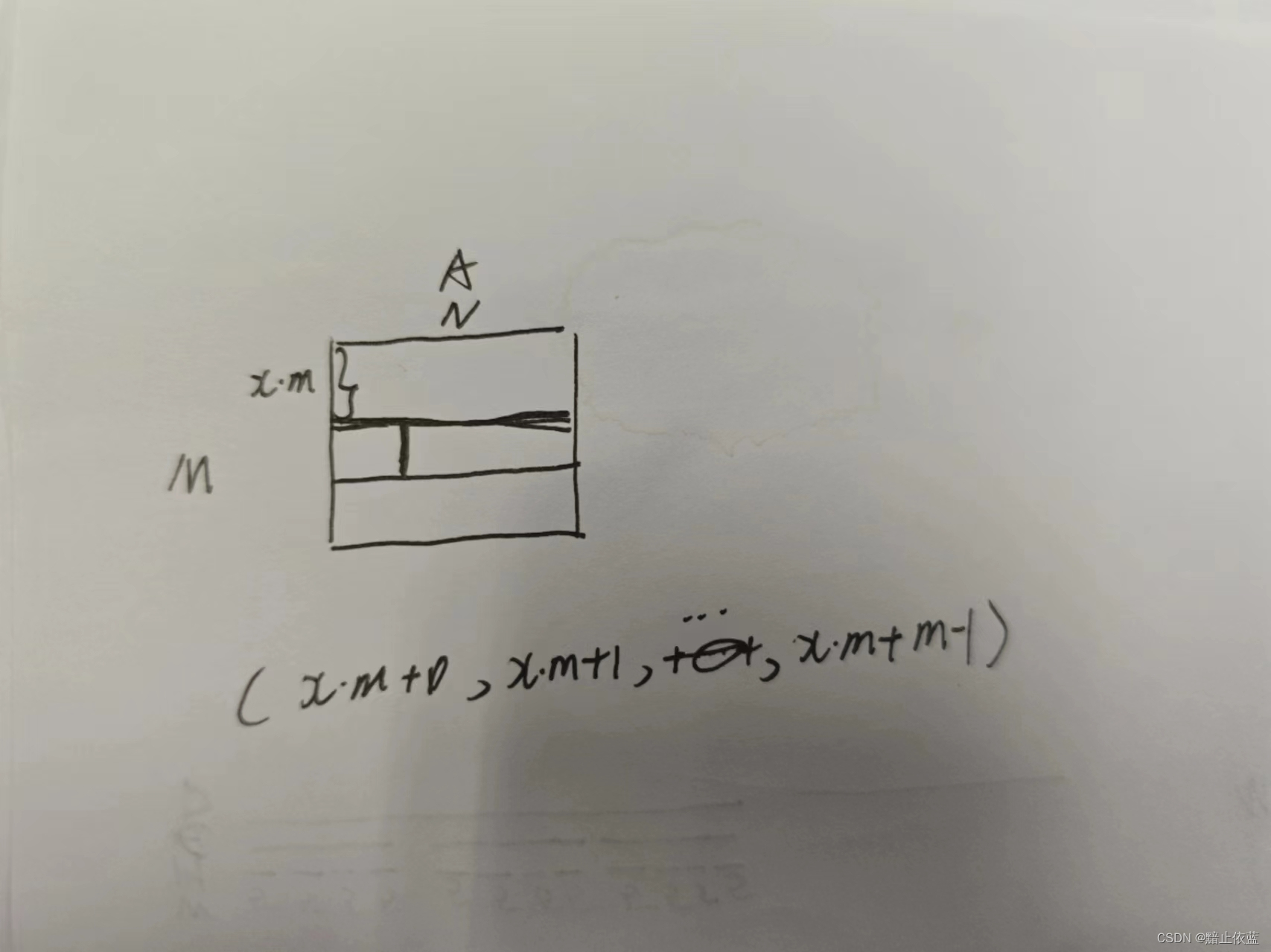
offs_am代表对应加载的a矩阵的那一行的第一块的每一行，在原来的a矩阵里的偏移

offs_am = (1*64+[0,63])%746 = [64,127]

这个数字乘以a矩阵的步数，就是从起始地址转到这一行，指针所需要的偏移量

假设起始指针地址是0，那么调到64行需要加64*stride_am指针偏移量

stride_am的意思是说，对于a矩阵，从(m,n)到(m+1,n)需要跨过的元素数量，其实就是n

这样就得到

[a_ptr+64*stride_am,a_ptr+65*stride_am,...,a_ptr+127*stride_am]T(转置，这是一个列向量)

为了得到小方块的所有指针偏移，需要二位扩展，a_ptr+x*stride_am相当于每一行的首地址，往左边一个元素，就是offs_k*stride_ak = [0,63]*1= [0,63],对于a矩阵，stride_ak是1，因为(m,n)到（m,n+1）只需要跨过一个元素

所以最终，我们可以得到这一套的指针矩阵

[a_ptr+64*stride_am,a_ptr+64*stride_am+1,...a_ptr+64*stride_am+63]

[a_ptr+65*stride_am,a_ptr+65*stride_am+1,...a_ptr+65*stride_am+63]

...

[a_ptr+127*stride_am,a_ptr+127*stride_am+1,...a_ptr+127*stride_am+63]

b矩阵的加载同理。

这里就好理解了，每次加载所需要二位矩阵块A和B对应数据，迭代乘累加