从暴力递归到动态规划（四）

题目一

给定一个二维数组matrix，一个人必须从左上角出发，最后到达右下角 沿途只可以向下或者向右走，沿途的数字都累加就是距离累加和 返回最小距离累加和

这题主要不是想谈动态规划，而是想谈一种技巧，这种技巧叫做动态规划的数组压缩技巧。

题目很好理解，也很简单，就是题目本身字面意思，举个栗子，如下图，箭头路线的累加和，因为它的累加和最小。这题应该算动态规划中最简单的一题了，我们想讲它不是因为要讲它动态规划的点，而是要讲一种技巧，这种技巧叫做数组压缩技巧

这道题我们当然可以从尝试入手，但因为这道题足够简单，足够经典，所以这里直接把它动态规划的代码给大家：

public static int mainPathSum1(int[][] m){
        if (m == null || m.length < 0 || m[0] ==null || m[0].length < 0){
            return 0;
        }
        int row = m.length;
        int col = m[0].length;
        int[][] dp = new int[row][col];
        dp[0][0] = m[0][0];

        for (int i = 1; i < row; i++) {
            dp[i][0] = dp[i-1][0] + m[i][0];
        }
        for (int i = 1; i < col; i++) {
            dp[0][i] = dp[0][i-1] + m[0][i];
        }
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1]) + m[i][j];
            }
        }
        return dp[row - 1][col - 1];
    }

就这题而言，一个原始的二维矩阵，我需要生成一个等规模的表，然后把它填好，浪费空间，如果原来是一个100 * 100 的二维矩阵的话，我还得生成一个 100 * 100的二维表出来，然后把它填好，我才能给你返回答案，于是我就想了，我想省点空间，比如一张dp表，一个随便的  i，j 位置，我依赖哪个位置，我只依赖我的左和上，比如一个位置17行，我是不是只需要依赖16行，15行和15行之上的表我是不是就不需要依赖了啊，我17行推出来之后，我18行是不是只需要17行，16行我不需要依赖啊。所以，这里面就存在优化空间的可能性。如下图所写，如此反复，就能求出右下角的值。这样不用整张大表，两个数组就够了。

                    

实际上还能够更省，一个数组就足够了，我的天，怎么一个数组就够了呢，我们继续看，已知一个普遍位置依赖我左边，依赖我上边，我只有一个数组叫arr，我们可以用arr自己推出dp第0行，肯定可以啊，第0行只会依赖左边就能得到，因为第0行没有上，这样我们就推出了第0行如下图

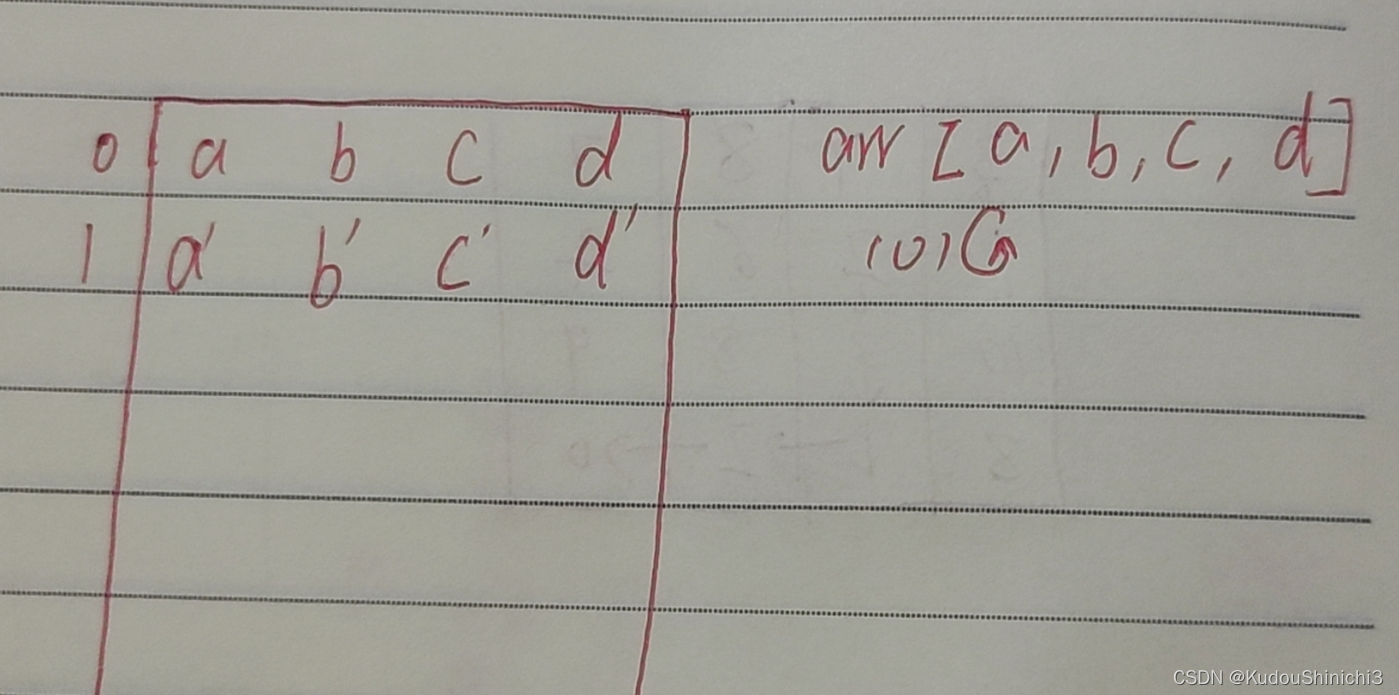
这是我能们就想，如果它能够自我更新，更新dp表中第一行的值，那岂不美哉，我们看a能不能顺利更新成a’，客观上来讲，这个a’只用依赖上边的a就能更新出来，a我们有，我们就能通过自己跟新出a’，现在arr中的a已经更新成a’了，我们怎么通过b更新出b’，我们先看b’需要啥，我们可以直观的看出，b’需要b的值和a’的值，我们会发现，b的左边就是已经更新完了的a’，而我自己就是还没更新的b，所以我们可以很顺利的更新出b’来，然后填回去。c d同理，这样一个数组自我更新，就可以一直下去。代码如下：

public static int mainPathSum2(int[][] m){
        if (m == null || m.length < 0 || m[0] ==null || m[0].length < 0){
            return 0;
        }
        int row = m.length;
        int col = m[0].length;
        int[] arr = new int[col];
        arr[0] = m[0][0];

        for (int i = 1; i < col; i++) {
            //填出第0行
            arr[i] = arr[i-1] + m[0][i];
        }
        //arr[0]  ->  dp[上一行][0]
       // 需要更新成   dp[这一行][0]
        for (int i = 1; i < row; i++) {
            arr[0] += m[i][0];
            for (int j = 1; j < col; j++) {
                //arr[j-1] -->  dp[这一行][j-1] 左侧的值
                // arr[j]   -->  dp[上一行][j]  的值
                arr[j] =  Math.min(arr[j-1],arr[j]) + m[i][j];
             }
        }
        return arr[col - 1];
    }

   这就完了吗？

当然没完，我们可以把它推广，不管是哪个动态规划，它只要依赖我左边，依赖我上边，我都能够这样搞，我们再看，如果一个动态规划，依赖我左上角的值和依赖我上边的值，我能不能够做数组压缩，当然可以，首先我们知道，我们不管什么问题，如果一个格子，它既依赖左上方，又依赖上方，那么对于第0行的值来说，他自己一定能够自己得到，对于第0列的值来说，它既不依赖左上角，也不依赖上，因为它既没有左上角，也没有上，不管 什么问题，面对第0行的值，肯定能直接得到，那么我们怎么得到第一行的值呢，你从右往左求嘛，我自己在没更新之前，我代表我上面的值，我左边还没更新呢，就代表我左上角的值啊，所以我把我自己给更新出来了。不管什么动态规划问题，只要满足这样一种依赖关系，都能够这么干。

好，我们再来一个疯狂的，假如任何一个动态规划问题，一个普遍位置，依赖我左，依赖我上，依赖我左上，怎么完成自我更新，依然可以完成自我更细，假如一个动态规划表，第0行依然可以搞出，而且每一个格子都依赖自己左边，为啥，因为它既没有左上，也没有上，还用上面这张图

首先 a能不能更新出a’ ,必然可以，为啥，因为a' 既没有左上，也没有左，它只依赖a，但是，我们在把a'填回去之前，我们拿一个变量，把这个a的值给记录一下，然后变成a',接下来b'可是要依赖三个位置，左边a'你有没有，有刚算过，你上边b有没有，有，你还没更新呢，你左上角a有没有，有，刚刚用变量记住了，所以增加一个变量之后可以把b顺利更新成b',但是更新之前，把这个变量释放掉，记录b。然后就能顺利完成一整行的更新。

假设一张dp表是 N  *  M的，假设我们用空间压缩，我们至少是不是得准备一个M列的数组啊，如果一个dp表有100万行，4列，空间压缩用着很爽，但如果是4行，100万列，我们是不是得准备100万长度滚动4会呀，还是不够省，如果是4行100万列，我们可以准备一个数组，横着更新。如下图：

当然有一点得说清楚，空间压缩技巧啊，是个小技巧，你有心情，你就做，你没有心情，就不做，我们写出来一方面是可以让大家认识到该技巧，另一方面可以用来装逼，他明明是一个二维的动态规划，却可以用一个数组来写出来。

题目二

arr是货币数组，其中的值都是正数。再给定一个正数aim。 每个值都认为是一张货币， 即便是值相同的货币也认为每一张都是不同的， 返回组成aim的方法数 例如：arr = {1,1,1}，aim = 2 第0个和第1个能组成2，第1个和第2个能组成2，第0个和第2个能组成2 一共就3种方法，所以返回3

看到这题，我们立马想到从左往右的尝试模型，这类模型我们也已经见识到很多题了。我们可以从左往右从index出发，index之后可以自由尝试。组成aim的方法数有多少

分析：我们先想写一个暴力递归，既然是从左到右的尝试模型，我们需要准备一个index参数，表示该位置之前不再考虑，该位置之后可以自由选择，接下来我们在考虑baseCase，肯定是index到最后啦，index到最后，如果能组成一个aim我们返回一种方法，否则就返回0，代码如下：

public static int coinWays(int[] arr,int aim){
        return process(arr,0,aim);
    }

    private static int process(int[] arr, int index, int rest) {
        if (rest < 0){
            return 0;
        }
        if (index == arr.length){
            return rest == 0 ? 1:0;
        }else {
            return process(arr,index+1,rest-arr[index]) +process(arr,index+1,rest);
        }
    }

尝试有了，根据之前文章，已经改很多遍动态规划了，这里就直接根据尝试进行动态规划的修改。

public static int dp(int[] arr,int aim){
        if (aim == 0){
            return 1;
        }
        int N = arr.length;
        int[][] dp = new int[N+1][aim + 1];
        dp[N][0] = 1;
        for (int index = N-1; index >= 0; index--) {
            for (int rest = 0; rest <= aim; rest++) {
                dp[index][rest] =  dp[index+1][rest] + (rest - arr[index] >= 0 ? dp[index+1][rest - arr[index]]:0);
            }
        }

        return dp[0][aim];
    }

题目三

arr是面值数组，其中的值都是正数且没有重复。再给定一个正数aim。 每个值都认为是一种面值，且认为张数是无限的。 返回组成aim的方法数 例如：arr = {1,2}，aim = 4 方法如下：1+1+1+1、1+1+2、2+2 一共就3种方法，所以返回3

这个问题是在之前问题进行了提升，我们还是先从尝试开始，这题是什么模型呢，还是从左往右的尝试模型，怎么尝试，从index出发，index之后的所有面值，可以自由选择，正好组成aim有多少方法数。

分析：怎么尝试？假如arr[5,2,10,20],aim = 1000，第一中选择，0张5元，然后去下一个位置继续搞定1000，第二种选择，1张5元，然后去下一个位置搞定 995，一直下去，总能得出结果。

public static int process1(int[] arr,int index,int rest){
        if (rest ==  arr.length){
            return rest == 0 ? 1:0;
        }
        int ways = 0;
        for (int zhang = 0; zhang * arr[index]  <= rest ; zhang++) {
            ways += process1(arr,index+1,rest-(zhang*arr[index]));
        }
        return ways;
    }

接下来开始改动态规划，肿么改，我们发现和上一题好像啊，无非就是上一题就两种选择，这一天是一个for循环的选择，依然是一个二维数组，和上面的动态规划大差不差，代码如下：

public static int dp1(int[] arr,int aim){
        if (arr == null || arr.length == 0 || aim < 0){
            return 0;
        }
        int N = arr.length;
        int[][] dp = new int[N+1][aim+1];
        dp[N][0] = 1;
        for (int index = N-1; index >=0 ; index--) {
            for (int rest = 0; rest <= aim ; rest++) {
                int ways = 0;
                for (int zhang = 0; zhang * arr[index]  <= rest ; zhang++) {
                    ways += dp[index+1][rest-(zhang*arr[index])];
                }
                dp[index][rest] = ways;
            }
        }
        return dp[0][aim];
    }

我们可以看出，咦，这里怎么有一个for循环，我们的递归就是这么写的，这么改有毛病吗？没毛病。我们之前所有题目，我们求一个格子都是O（1）的过程，而这道题不一样，求一个格子，得干出一个for循环出来，这道题我们用记忆化搜索方法，和我们改成了严格表结构的方法，它整体肯定是比暴力搜索要好的，记忆化搜索就是我如果算过，直接拿值，没算过就去算，而严格表结构是我从简单到复杂，我严格规定先算哪个后算哪个。那他们的时间复杂度呢，如果单独一个格子没有枚举行为，什么是枚举行为，就是没有for循环，他只依赖于有限的位置，记忆化搜索和严格表结构的答案同样的好，如果有枚举行为，我们就需要搞出严格表结构后继续优化。

如上图，假如 i 是3元，假如我想求对号位置，根据递归我们可以看出，如果我们想要求出第i行这个对号，我们是需要求出第i+1行 a+b+c+d+e的和才能得出对号的值，我们仔细观察，这个星号当初我们求的时候它依赖那些格子，是不是 b+c+d+e,那我们求对号的时候为什么要再加一遍呢，我们直接用 a+星号不就可以了嘛，知道为啥要建立严格表依赖结构了吧，我们把枚举行窃给省略了。所以我们改一下。

public static int dp2(int[] arr,int aim){
        if (arr == null || arr.length == 0 || aim < 0){
            return 0;
        }
        int N = arr.length;
        int[][] dp = new int[N+1][aim+1];
        dp[N][0] = 1;
        for (int index = N-1; index >=0 ; index--) {
            for (int rest = 0; rest <= aim ; rest++) {
                dp[index][rest] = dp[index + 1][rest];
                if (rest - arr[index] >= 0){
                    dp[index][rest] += dp[index][rest-arr[index]];
                }
            }
        }
        return dp[0][aim];

for循环省了，时间复杂度也少了一层，这样我们不就能拿出去装逼了嘛。

题目四

arr是货币数组，其中的值都是正数。再给定一个正数aim。 每个值都认为是一张货币， 认为值相同的货币没有任何不同， 返回组成aim的方法数 例如：arr = {1,2,1,1,2,1,2}，aim = 4 方法：1+1+1+1、1+1+2、2+2 一共就3种方法，所以返回3

这道题就是把题目三的张数收集一下，不再是无限了，这道题我们看怎么试，我们可以准备两个数组，第一个arr我们的面值数组，去一下重{1,2}排不排序无所谓，第二个是我们的张数数组{4,2}，接下来开始写递归尝试，怎么尝试，我们先把原来的数组调整成刚刚说的两个数组，接下来就和原来的一样了，但是有一点得注意，循环的条件是我既不能超过超过总钱数aim，也不能超过每张的张数。

public static class Info{
        public int[] coins;
        public int[] zhangs;

        public Info(int[] coins, int[] zhangs) {
            this.coins = coins;
            this.zhangs = zhangs;
        }
    }

    public static Info getInfo(int[] arr){
        HashMap<Integer,Integer> counts = new HashMap<>();
        for (int value:arr) {
            if (!counts.containsKey(value)){
                counts.put(value,1);
            }else {
                counts.put(value,counts.get(value)+1);
            }
        }
        int N = counts.size();
        int[] coins = new int[N];
        int[] zhangs = new int[N];
        int index = 0;
        for (Map.Entry<Integer,Integer> entry:counts.entrySet()) {
            coins[index] = entry.getKey();
            zhangs[index++] = entry.getValue();
        }
        return new Info(coins,zhangs);
    }

    public static int coinsWay(int[] arr,int aim){
        if (arr == null || arr.length == 0 || aim < 0){
            return 0;
        }
        Info info = getInfo(arr);
        return process(info.coins,info.zhangs,0,aim);
    }
    //coins  面值数组，整数且去重
    //zhangs  面值数组对应的张数数组
    public static int process(int[] coins,int[] zhangs,int index,int rest){
        if (index == coins.length){
            return rest == 0 ? 1 : 0;
        }
        int ways = 0;
        for (int zhang = 0; zhang * coins[index] <= rest && zhang <=zhangs[index] ; zhang++) {
            ways += process(coins,zhangs,index+1,rest-(zhang*coins[index]));
        }
        return ways;
    }

接下来改动态规划有意思了，他跟第三题不一样如下图

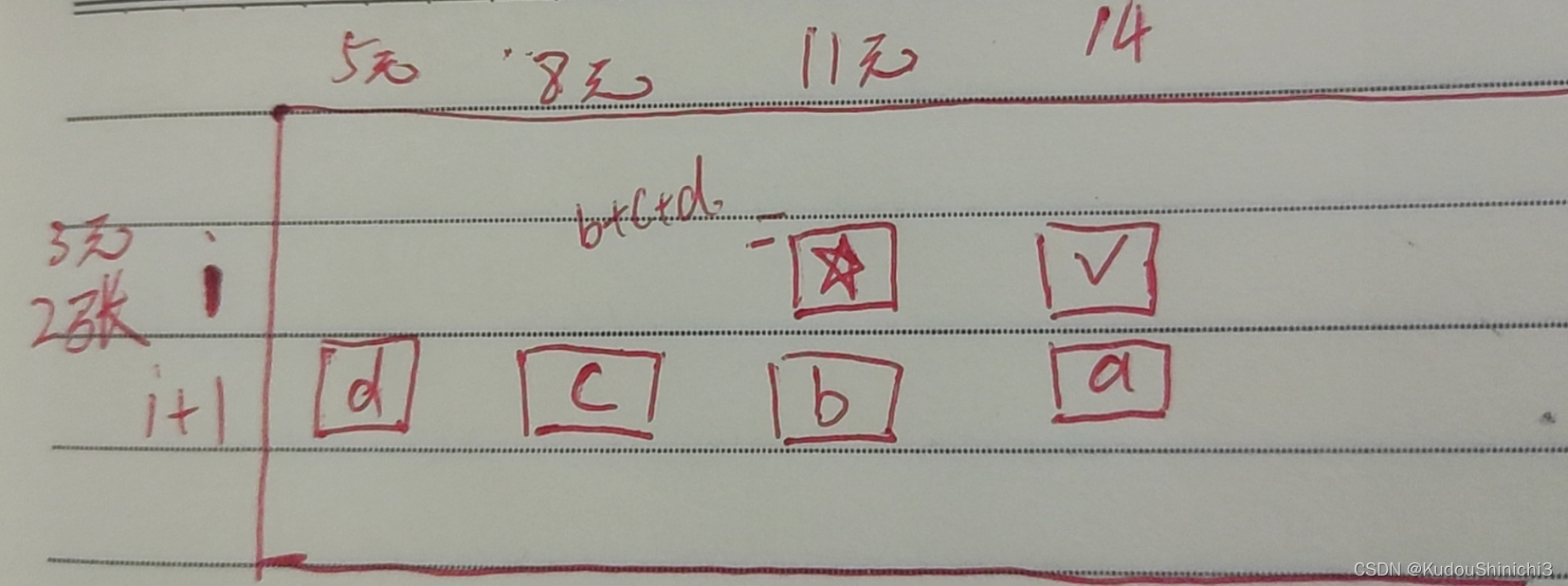
我们求i，14这个格子，0张的时候我们依赖a,1张的时候我们依赖11,2张的时候我们依赖8，我们不再依赖8元左边的了，为啥，因为你只有两张，然后我们很自然的想到星号了，星号除了依赖b,依赖c,它还依赖5元的d因为它也能用两张啊，所以星号是 b + c + d， 所以如果对号加星号回多算一个d的，因为对号只有两张，它用不着d。所以怎么办，对号等于星号+a单减一个d。

public static int dp3(int[] arr,int aim){
        if (arr == null || arr.length == 0 || aim == 0){
            return 0;
        }
        Info info = getInfo(arr);
        int[] coins = info.coins;
        int[] zhangs = info.zhangs;
        int N = coins.length;
        int[][] dp = new int[N+1][aim + 1];
        dp[N][0] = 1;
        for (int index = N - 1; index >= 0; index--) {
            for (int rest = 0; rest <= aim; rest++) {
                dp[index][rest] = dp[index+1][rest];
                if (rest - coins[index] >= 0){
                    dp[index][rest] += dp[index][rest-coins[index]];
                }
                if (rest - coins[index] * (zhangs[index] + 1) >= 0){
                    dp[index][rest] -= dp[index+1][rest-coins[index] * (zhangs[index] + 1)];
                }
            }
        }
        return dp[0][aim];
    }