堆 和 优先级队列（超详细讲解，就怕你学不会）

---

一、堆的概念特性

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆（大根堆）；每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆（小根堆）。

从堆的概念可知，堆是一棵完全二叉树，因此可以使用层序的规则采用顺序的方式来高效存储：

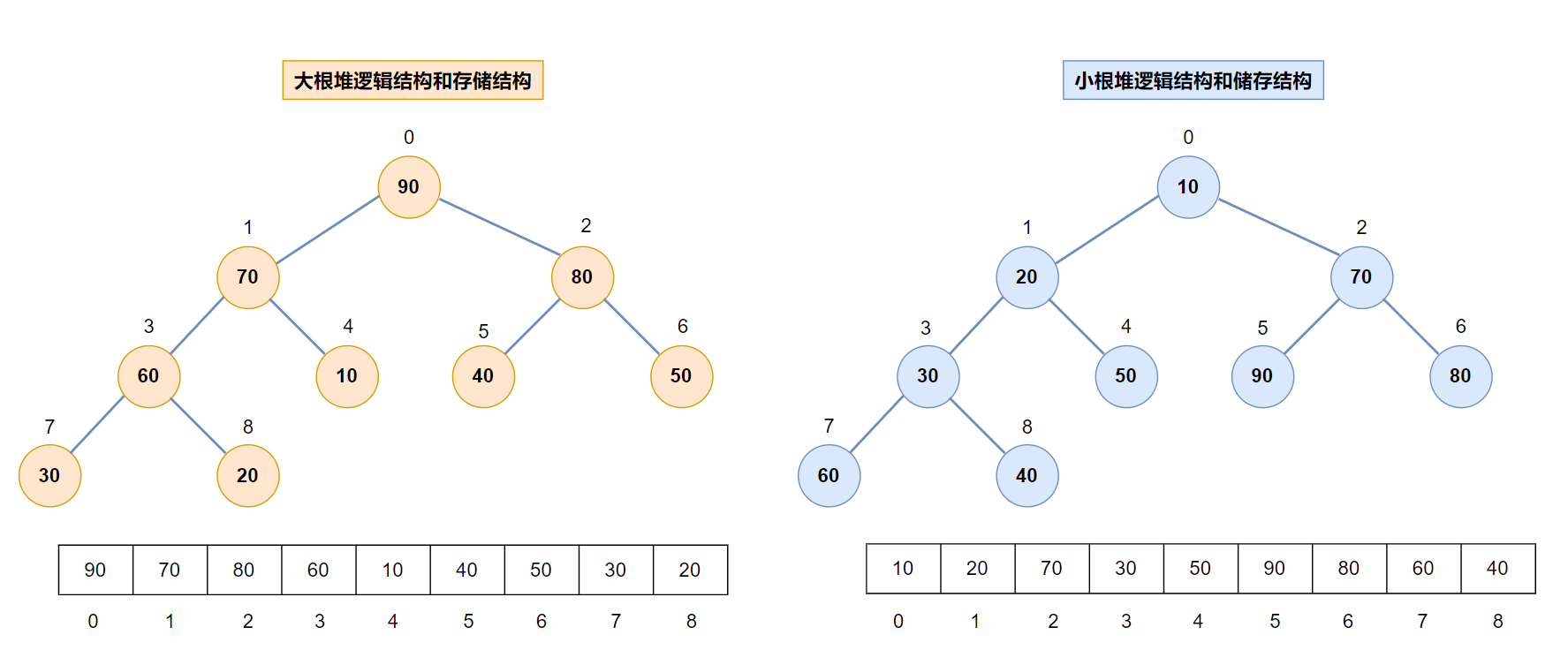
将元素存储到数组中后，可以根据二叉树的性质对树进行还原：

假设i为节点在数组中的下标，则有：

1. 如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
2. 如果2 * i + 1小于节点个数（左孩子存在条件），则节点i的左孩子下标为2 * i + 1，否则没有左孩子
3. 如果2 * i + 2 小于节点个数（右孩子存在条件），则节点i的右孩子下标为2 * i + 2，否则没有右孩子

二、堆的创建

1、向下调整算法

示例：将集合{75,20,70,30,50,90,80,60,40}调整为小根堆

通过分析，已知集合的 “左右子树均满足小堆的性质” ，我们只需要将根节点向下调整到合适的位置，使集合整体为小堆即可。具体来说，我们可以细化为如下调整方法：

1. 每次调整以待调整结点、它的左右孩子结点构成的子树为单元进行“向下调整”
2. 每个单元以待调整结点为根节点，将左右孩子结点的最小值（小堆）和根节点进行比较，如果根节点<min(左孩子，右孩子)调整结束，否则，待调整根节点和[min(左孩子，右孩子)]交换，交换完成后，继续重复这个步骤直到待调整结点为当前子树单元中的最小值，或待调整结点不在存在孩子结点，调整结束。

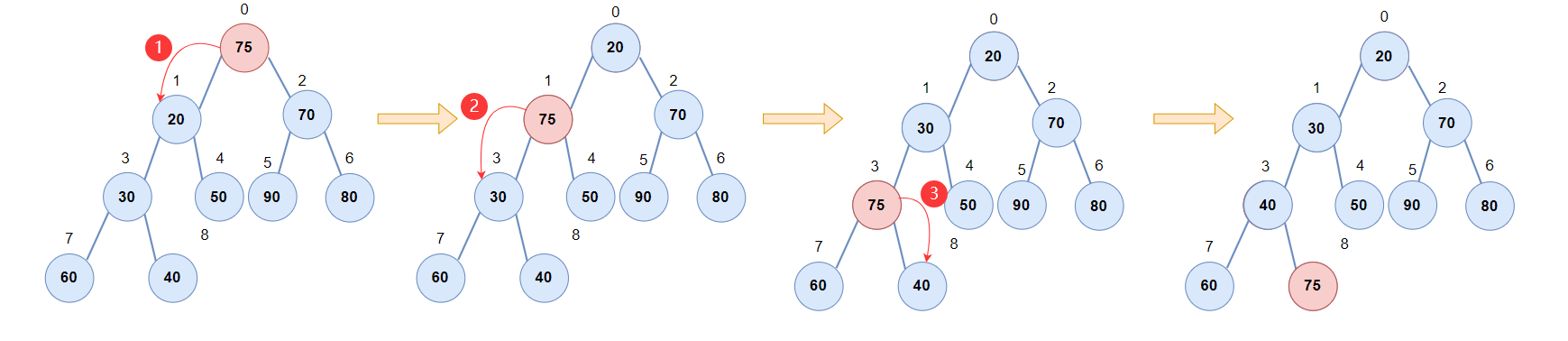
按照以上思路，下面是详细的代码实现：

	/**
     * 小根堆->向下调整算法
     * @param parent 待调整结点
     * @param len 数组长度
     */
    private void shiftDown(int[] array,int parent, int len) {
   
   
        int child = 2 * parent + 1;//根据完全二叉树性质，找到左孩子
        while (child < len) {
   
   
        	//child<len判断孩子合法性
            //满足child<len至少存在左孩子
            if (child + 1 < len && array[child] > array[child + 1]) {
   
   
            	//存在右孩子，且右孩子为左右孩子最小值
                child++;
            }
            //此时child一定是左右孩子的最小值的下标
            if (elem[child] < elem[parent]) {
   
   
            	//满足条件，就交换
                int tmp = array[parent];
                array[parent] = array[child];
                array[child] = tmp;
				//交换完成后，继续以新的位置向下调整
                parent = child;
                child = 2 * parent + 1;
            } else {
   
   
            	//array[parent] < array[child]调整结束
                break;
            }
        }
    }

小结：

1. 在调整以parent为根的二叉树时，必须要满足 parent 的左子树和右子树已经是堆了才可以向下调整。
2. 向下调整算法的最坏情况为从根一直比较到叶子，比较的次数为二叉树的高度，时间复杂度为O(log₂N)。

2、向下调整建堆

在上面的探讨中，我们知道可以使用向下调整算法，将左右子树为堆的完全二叉树序列调整为堆，那么如果给出任意的完全二叉树序列（左右子树不满足堆的特性），我们又该如何调整为堆呢？

思路： 我们已知使用向下调整算法，parent的左右子树必须满足堆的特性，对于任意普通完全二叉树序列，显然不能直接使用向下算法进行调整。不过我们知道一颗完全二叉树是由一颗颗左右子树构成的，虽然一颗普通的完全二叉树不能直接使用向下调整算法，但是倒数第一个非叶子结点构成的子树一定可以使用向下调整算法，所以如果我们可以先将下面的子树调整为堆，在继续对子树的根结点进行调整，这样根节点的左右子树就满足了堆的特性，可以直接使用向下调整算法。就这样一直向上对根结点进行向下调整，直到0下标对应的根节点调整完毕，整颗完全二叉树序列就满足了堆的特性了。

例如以序列{50,70,40,90,20,10,80,30,60}为例，调整后为{10,20,40,30,70,50,80,90,60}

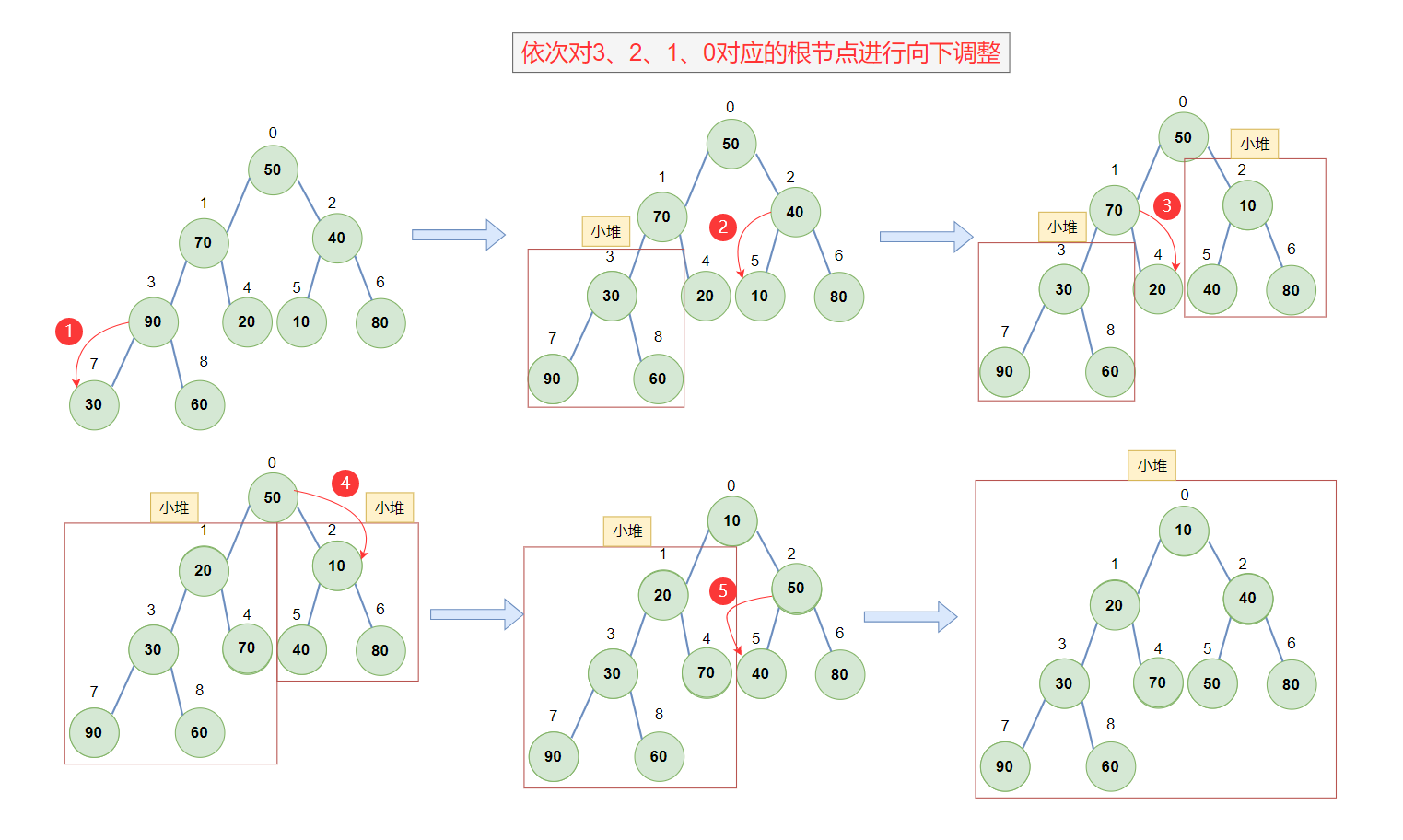
具体实现：

    /**
     * 向下调整建堆
     * @param array
     */
    public void creatHeap(int[] array) {
   
   
    	//清晰了思路之后，建堆就非常简单了
    	//只需从最后一个非叶子结点开始，直到找到下标为0的根节点
    	//每遇到一个结点向下调整，调用shiftDown即可
        for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {
   
   
            shiftDown(array,parent,array.length);   	 	
        }
    }

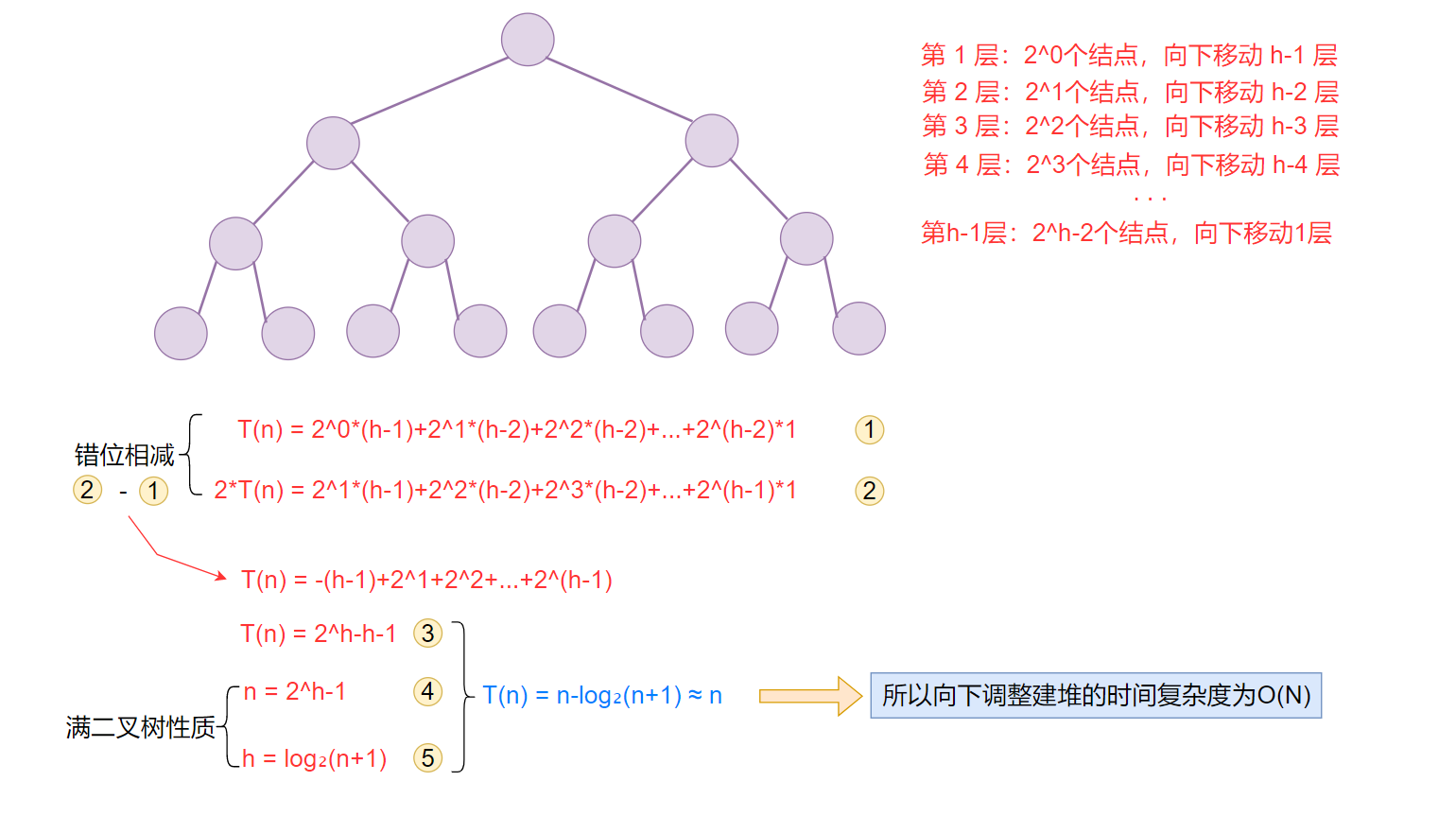
3、向下调整建堆的时间复杂度

假设序列为满叉树，假设树高为h，则最坏情况下第K层的2^(k-1)个结要向下移动h-k层。

三、堆的插入

1、向上调整算法实现插入

堆的插入相对来说较为简单，主要分为以下两步：

1. 每次将新节点插入到堆的