数据结构与算法：磁盘存储索引的B树与B+树

1. B树的应用场景和实用特点

  B树（balance tree）和B+树应用在磁盘存储索引，可以认为是m叉的多路平衡查找树，但是从理论上讲，二叉树查找速度和比较次数都是最小的，为什么不用二叉树呢？

因为我们要考虑磁盘IO的影响，它相对于内存来说是很慢的。数据库索引是存储在磁盘上的，当数据量大时，就不能把整个索引全部加载到内存了，只能逐一加载每一个磁盘页（对应索引树的节点）。所以我们要减少IO次数，对于树来说，IO次数就是树的高度，而“矮胖”就是b树的特征之一，它的每个节点最多包含m个孩子，m称为b树的阶，m的大小取决于磁盘页的大小。

  B/B-树（balance tree）与B+的差别：没有B-树，B-树和B树是同一种意思。

  数据存储不同：B树的每一个节点都用是来存储数据的；B+树的内节点不存储数据，用来做索引的，所有的数据都存储在叶子节点中。
  数据查询不同：B树在找到具体的数值以后，则结束，而B+树则需要通过索引找到叶子结点中的数据才结束，也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。

2. B树的定义

  B树是一颗多叉树，但对节点的数量，与叶子节点的高度做了约束

一颗M阶B树T，满足以下条件

1. 每个结点至多拥有M课子树
2. 根结点至少拥有两颗子树
3. 除了根结点以外，其余每个分支结点至少拥有M/2课子树
4. 所有的叶结点都在同一层上
5. 有k课子树的分支结点则存在k-1个关键字，关键字按照递增顺序进行排序
6. 关键字数量满足ceil(M/2)-1 <= n <= M-1

3. B树叶子节点的前后指针

4. B树插入的两种分裂

  添加一个新节点为什么需要对B树进行分裂？

  添加一个新节点可能会破坏一颗B树的性质：每个节点至多拥有M颗子树，并且有k颗子树的分子节点存在k-1个关键字，也就是说一颗M阶树每个节点最多只能有M-1个关键字。当向一个有M-1个关键字的节点添加一个新节点，这个时候就会破坏B树的性质，此时需要对B树进行分裂。

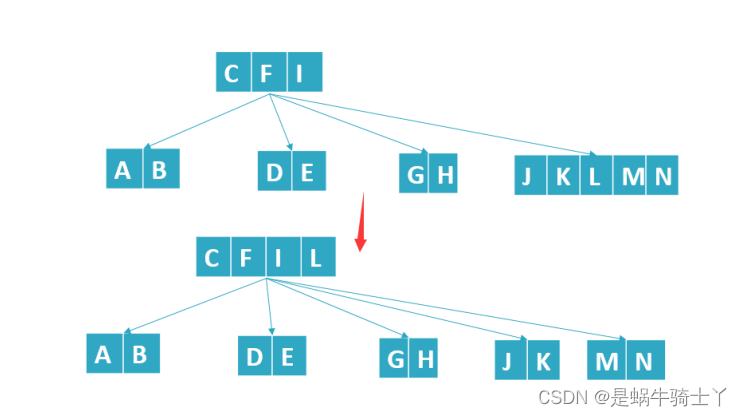
4.1 节点分裂

1. 创建一个空节点节点来存储分裂后多出来的一个新节点
2. 将分裂节点的右边的节点添加到创建的空间点
3. 将分裂的节点添加到父节点中，需要对父节点的保存节点进行移位

4.2 根节点分裂

1. 创建一个空节点作为根节点的父节点
2. 对根节点进行节点分裂操作
   
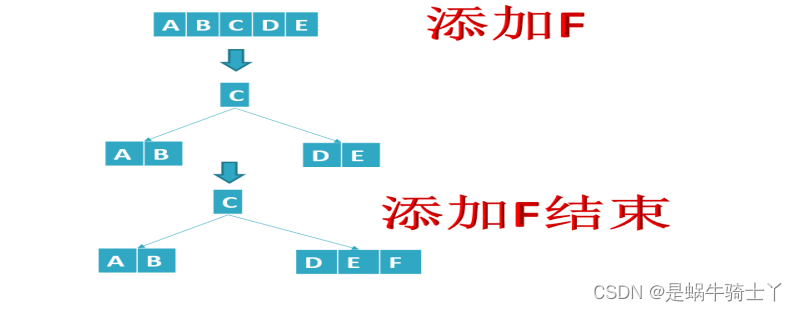
     注意：添加节点的时候，先判断是否要分裂，分裂后在添加新节点，并且新节点的添加位置为叶子节点。
   

void btree_split_child(btree *T, btree_node *x, int i) {
   
	int t = T->t;
	
	btree_node *y = x->childrens[i];
	//创建一个空节点节点来存储分裂后多出来的一个新节点
	btree_node *z = btree_create_node(t, y->leaf);
	z->num = t - 1;
	
	//将分裂节点的右边的节点添加到创建的空间点
	int j = 0;
	for (j = 0;j < t-1;j ++) {
   
		z->keys[j] = y->keys[j+t];
	}
	if (y->leaf == 0) {
   
		for (j = 0;j < t;j ++) {
   
			z->childrens[j] = y->childrens[j+t];
		}
	}
	
	// 将分裂的节点添加到父节点中，需要对父节点的保存节点进行移位
	y->num = t - 1;
	for (j = x->num;j >= i+1;j --) {
   
		x->childrens[j+1] = x->childrens[j];
	}

	x->childrens[i+1] = z;

	for (j = x->num-1;j >= i;j --) {
   
		x->keys[j+1] = x->keys[j];
	}
	x->keys[i] = y->keys[t-1];
	x->num += 1;
	
}
//添加节点的时候，先判断是否要分裂，分裂后在添加新节点，并且新节点的添加位置为叶子节点。
void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) {
   

	int i = x->num - 1;

	if (x->leaf == 1) {
   	//叶子节点直接插入
		
		while (i >= 0 && x->keys[i] > k) {
   
			x->keys[i+1] = x->keys[i];
			i --;
		}
		x->keys[i+1] = k;
		x->num += 1;
		
	} else {
   		//递归到叶子节点那一层添加新节点
		while (i >= 0 && x->keys[i] > k) i --;
		//判断子节点是否需要分裂
		if (x->childrens[i+1]->num == (2*(T->t))-1) {
   
			btree_split_child(T, x, i+1);
			if (k > x->keys[i+1]) i++;
		}

		btree_insert_nonfull(T, x->childrens[i+1], k);	
	}
}

void btree_insert(btree *T, KEY_VALUE key) {
   
	//int t = T->t;

	btree_node *r = T->root;
	if (r->num == 2 * T->t - 1) {
   	//叶子节点的分裂
		
		btree_node *node = btree_create_node(T->t, 0);
		T->root = node;

		node->childrens[0] = r;

		btree_split_child(T, node, 0);

		int i = 0;
		if (node->keys[0] < key) i++;
		btree_insert_nonfull(T, node->childrens[i], key);
		
	} else {
   
		btree_insert_nonfull(T, r, key);
	}
}

5. B树删除的前后借位与节点合并

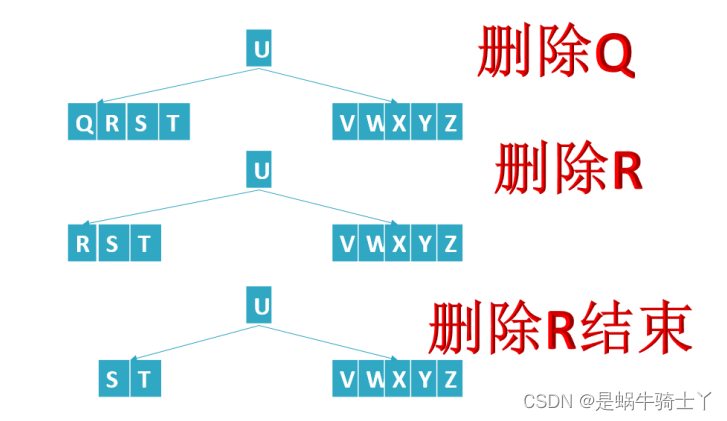
5.1 删除节点是叶子节点，直接删除

  此处大家可能会存在一个疑惑：如果删除的节点是叶子节点就直接删除，那会不会导致这个叶子节点的关键字的数量少于T。答案是不会的。规律：合并/借位 —> 删除因为在删除这个叶子节点之前会对这个叶子节点上面的关键字的数量进行判断，如果叶子节点关键字的数量少于T，会对这个叶子节点进行调整，调整的方式有：前后借位与节点合并。

if (idx < node->num && key == node->keys[idx]) {
   

		if (node->leaf) {
   
			
			for (i = idx;i < node->num-1;i ++) {
   
				node->keys[i] = node->keys[i+1];
			}

			node->keys[node->num - 1] = 0;
			node->num--;
			
			if (node->num == 0) {
    //root
				free(node)