动态规划算法分析及实例——求解完全背包问题（java实现）_多起点多终点的最短路径动态规划-CSDN博客

本文链接：https://blog.csdn.net/LKPchengxuyuan/article/details/71512271

一、动态规划算法简介

动态规划算法和分治法类似，都是把子问题的解组合从而求解原问题。但分治法是将一个问题划分为互不相交的子问题，递归地求解子问题，再将他们的解组合起来，求出原问题的解。而动态规划算法针对的是子问题重叠的情况，即不同的子问题中还有公共的子问题，也就是说子问题的求解是递归进行的，还可以将子问题划分为更小的子问题。在这种情况下，分治法就会做很多不必要的工作，去反复地求解那些公共子问题。而动态规划算法对所有的子问题只求解一次，并且将每一次所得的解保存在一个表格中，这就避免了很多不必要的计算。

动态规划算法通常用来求解最优化问题。这类问题可能有很多可行的解，每个解都有一个值，而我们要找的就是其中具有最优值的解，这样的解就被称为问题的一个最优解，而不是全局的最优解，因为可能有多个解都有最优值。

二、动态规划算法的设计思想

为了理解动态规划算法的基本思想，我们先来看一个简单的例子。本例取自屈婉玲《算法分析与设计（第二版）》（清华大学出版社）。

（一）多起点、多终点的最短路径问题

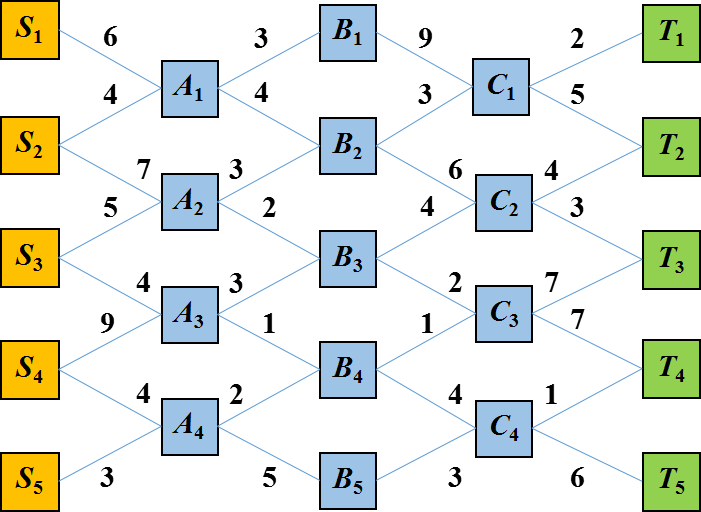
在实际问题中，我们经常会遇到路径选择的问题。如图所示，有5个起点S₁，…，S₅，5个终点T₁，…，T₅，其余结点是途经结点。各结点之间用边连接，边上的整数表示长度。从起点S_i可以通过4条从左到右的边S_i→A_j→B_k→C_l→T_m到达终点T_m，这就是一条从起点S_i到终点T_m的路径，路径的长度就是这4条边的长度之和。我们的问题是：给定道路图，在所有起点到终点的路径中找一条长度最短的路径。

实际上这个问题用穷举法就可以解决，我们可以列举出每一个起点到每一个终点的所有可能路径，然后从中选取最短的一条路径。但是结点数目比较多的时候，时间上的消耗可能难以承受。

我们可以尝试用动态规划算法来解决这个问题。从终点向起点回推，把求解过程分成4步，每一步对应的子问题的终点不变，但起点逐步前移，使得前一步已经求解的问题恰好是后面新问题的子问题，到最后一步求解的最大的子问题即为原始问题。具体来说，所有子问题的终点都是T_m，但起点不同。第一步子问题的起点是C_l，第二步子问题的起点是B_k，第三步子问题的起点是A_j，第四步子问题的起点是S_i，求解到第四步的时候，其实已经是原始问题了。那么每一步需要求解的就是：从当前起点到终点的最短路径和长度。