1、判断一棵树是否是完全二叉树;
2、求二叉树中最远两个结点的距离;
3、由前序和中序遍历序列重建二叉树 (前序序列:1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5);
4、求二叉树两个结点的最近公共祖先;
5、将二叉搜索树转化成有序的双向链表;
判断一棵树是否是完全二叉树
要想判断一颗树是否是完全二叉树,你得先知道什么是完全二叉树。
完全二叉树:
①若树的高度为h,则除第h层,上面的h-1层都是达到最大个数。
②第h层的结点都集中在最左边。
当你知道了完全二叉树的性质,这道题就好做了。有很多种解法。这里我给出一种使用
队列的解法。
我们先看一下完全二叉树与非完全二叉树的区别:
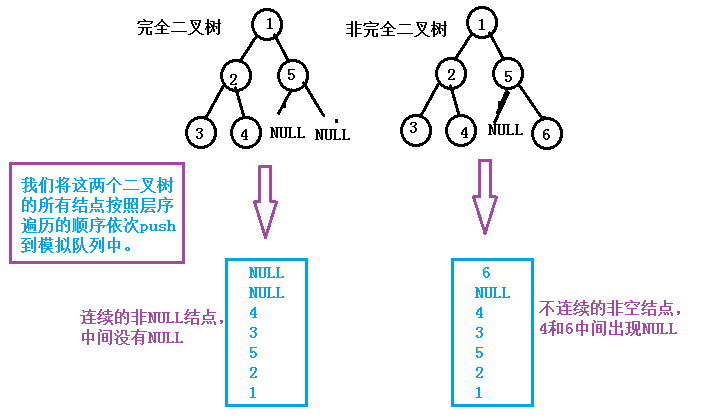
我们可以看到,
将完全的二叉树的所有结点push到队列里之后,有连续的非NULL结点。中间没有NULL打断。而非完全二叉树非空结点之间右NULL打断。我们可以根据这一区别来判断一棵树是否是完全二叉树。
代码:
//队列法
//队列法
bool IsCompleteTree()
{
if (_root == NULL)
{
return true;
}
Node* root = _root;
queue<Node*> q;//建立队列
q.push(root);//先将根节点入队列
//层序遍历,将结点依次入队列
while (1)
{
q.push(root->_left);
q.push(root->_right);
q.pop();
if (q.front() != NULL)
{
root = q.front();
}
else
{
break;//遇到空结点就退出循环
}
}
//遇到空结点,判断后面是否还有空结点
while (!q.empty())
{
Node* ret = q.front();
if (ret != NULL)
{
return false;
}
q.pop();
}
return true;
}
还有一种时间空间复杂度较为复杂的解法,使用了递归。我将代码放到这里,感兴趣的可以研究下。
递归法:
//递归法
bool IsCompleteTree()
{
if (_root == NULL)
{
return true;
}
return __IsCompleteTree(_root);
}
//递归判断
bool __IsCompleteTree(Node* root)
{
if (root == NULL)
{
return true;
}
if (root->_left == NULL && root->_right != NULL)
{
return false;
}
//递归,求每一个节点的左右高度
int left = __GetHigh(root->_left) + 1;
int right = __GetHigh(root->_right) + 1;
if (left - right > 1)//当其中某个节点的左右高度差大于1的时候,就不满足完全二叉树
{
return false;
}
return __IsCompleteTree(root->_left) && __IsCompleteTree(root->_right);
}
求二叉树中最远两个结点的距离
看到这个题,一般大家会有一个思想误区:最远的两个结点是左子树最深结点和右子树最深结点。不是!千万不要这样想!
最远结点,即为相距路径最长的两个结点,例如下面两种情况:
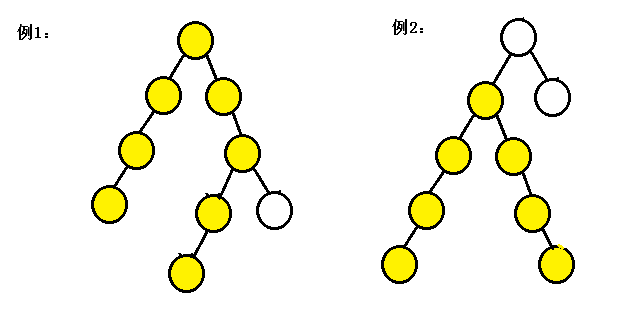
最优解法:利用递归(
后序递归),划分子问题。
子问题模型:传一个全局变量Max(最远距离),初值设为0,传参类型为传引用。求取当前结点cur左右子树的深度并进行比较,返回较深的子树的深度的值。在返回前,将左右子树的深度相加求的和,与Max进行比较,若和大于Max,将和的值赋给Max。
例如:
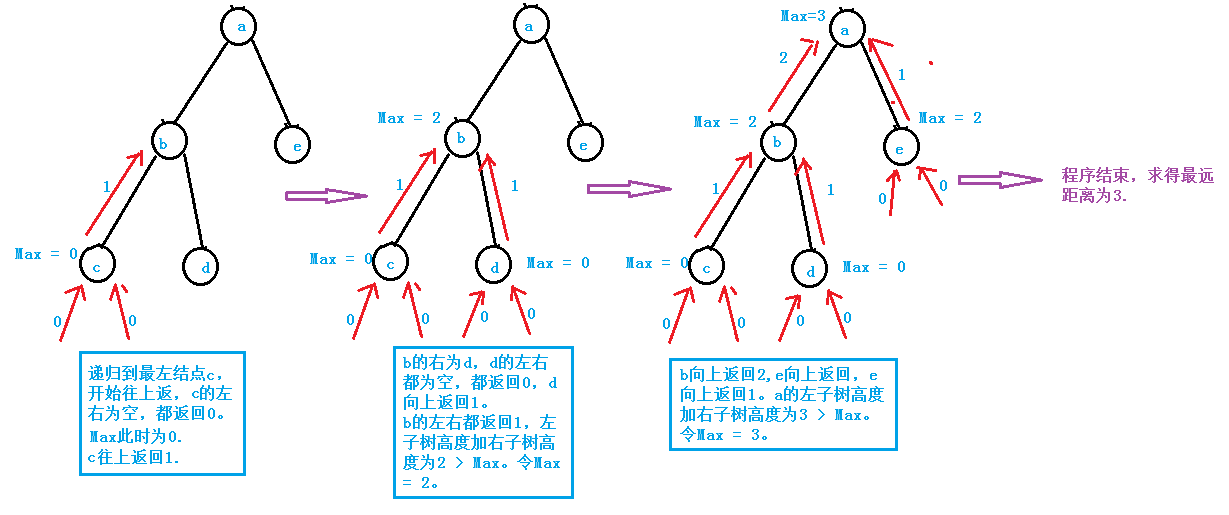
我们在写代码的时候不要递归到一个结点就对其左右子树求高度。这样会大大增加工作量,降低了程序的效率。采用后序递归,先递归左子树,再递归右子树。将子树高度层层返回,会是最优的解法。令时间复杂度达到O(N)。
<








 本文涵盖了五道经典的二叉树面试题目,包括判断是否为完全二叉树、求最远结点距离、从前序和中序遍历重建二叉树、寻找最近公共祖先以及将二叉搜索树转化为有序双向链表。对于每道题目,文章详细阐述了解题思路和方法。
本文涵盖了五道经典的二叉树面试题目,包括判断是否为完全二叉树、求最远结点距离、从前序和中序遍历重建二叉树、寻找最近公共祖先以及将二叉搜索树转化为有序双向链表。对于每道题目,文章详细阐述了解题思路和方法。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 444
444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








