Java数据结构:初识二叉树-CSDN博客

树🌳：

定义

树由节点（Node）和边（Edge）组合而成，其中有一个特定的根节点（Root），其余节点被分成若干个互不相交的子树

一颗树最重要的就是树根，不断从土壤中汲取养分，在主干上分出大大小小的树杈，树杈上点缀着片片叶片。
对于树型结构来说同样，有一个根节点（树根或树干）
一个结点可以延伸出多个节点（树杈）
【延伸出的结点称为子节点
被延伸的结点称为父节点】
N个节点，N-1 条边

任何一个子节点有且仅有一个父节点
任何一个父节点可以包含多个子节点

例子：

给大家一个形象的例子：选修高中政治的一定给红楼贾府众人牵过红线吧

宝玉黛玉在现行的婚姻法下能结婚吗？
显然不行这里荣国公贾源为根
贾母是其儿媳是其子节点
贾赦，贾政，贾敏是贾母的子节点
黛玉和宝玉是堂兄弟结点有同一个爷节点（贾母）三代旁系血亲不能结婚
一个人只能有一个父亲
却可以有多个兄弟姐妹

说回正题

树的相关概念

节点的度：节点拥有的子节数目。例如，若某节点有 3 个子节点，其度为 3
树的度：树中所有节点度的最大值。一棵树中可能有多个节点，树的度由最大的节点度决定
叶子节点/终端结点：度为零的节点反之为非叶子节点/终端结点
双亲结点/父节点：含有子节点的节点
根节点：一棵树中，没有子节点的节点
节点的层次：从根节点开始定义根为第 1 层，其子节点为第 2 层，依此类推，层次从顶至底递增
树的高度/深度：树节点的最大层次
兄弟节点：具有相同的父节点
堂兄弟节点：父节点在同一层次的节点互称堂兄弟，具有同一个爷节点
节点的祖先：从根节点到该节点所经分支上的所有节点
子孙：根节点以外的所有节点
森林：由多棵互不相交的树组成的集合，可看作删除根节点后各子树构成的森林。

树的表示形式：

表示树与表示链表相似

链表：
1. 一个表示是节点的类 —> 每个节点保存一个next
2. 拿到头节点就能拿到后续的节点

数：
1.有一个表示节点的类
2. 拿到根节点就能拿到后续的节点

代码表示n叉树

双亲表示法

class Node{

String val; // 特定场景使用

Node parent;

}

孩子表示法

class Node{

String val; // 常用

List<Node> children;

}

孩子双亲表示法

class Node{

String val; // 常用

List<Node> children;

Node parent;

}

孩子兄弟表示法

class Node{

String val; // 特定场景使用

Node firstChild;

List<Node> brotherNodes;

}

二叉树：

定义：

二叉树，任意节点的度，不能超过2

以上四种情况都是二叉树

满二叉树

整个树，没有只存在于个分支的情况

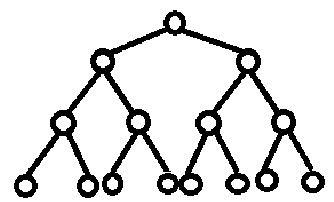
完全二叉树
特点

叶子结点位置：叶子结点只可能在最大的两层上出现1。
子树深度关系：对任一结点，如果其右子树的最大层次为 L，则其左子树的最大层次为 L 或 L+1。
结点度数限制：至多只有最下面的两层上的结点度数可以小于 2。
最后一层结点分布：最后一层的结点都集中在该层最左边，右边的若干结点可以缺失1。

二叉树的性质：

1.若规定根节点的层数为1，则一颗非空二叉树的第i层上最多有2^(i-1)个节点（i > 0）。
2.若规定只有根节点的二叉树的深度为1，则深度为K的二叉树的最大节点数 2^k - 1。
3.对任何一棵二叉树，如果对其节点个数为N0，度为2的非叶节点个数为N2，则有N0=N2+1。
4.具有N个节点的完全二叉树的深度 K 为log2(N+1)，(以2为底)向上取整。
5.对于具有N个节点的完全二叉树，如果按照从上至下，从左至右的顺序对所有节点从0开始编号，则对于序号为 i 的节点有:
若 i > 0, 双亲序号：（i - 1）/ 2; i = 0, i为根节点编号，无双亲节点
若 2i + 1 < n, 左孩子序号：2i + 1, 否则无左孩子
若 2i + 2 < n, 右孩子序号：2i + 2, 否则无右孩子

二叉树的存储：

孩子表示法

存储二叉树只需要将左右孩子的引用指向其对应的孩子

class Node { // 某个节点只有左子树，没有右子树

String val; right == null;

Node left; // 右子树

Node right; // 左子树

}

// 表示一个二叉树的节点
class Node {
    public String val;
    public Node left;
    public Node right;

    public Node(String val){
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

// 可以通过一个根节点，就能拿到整个树了
// 既可以用 Node root 表示
// 也可以创建一个新的类，在类中持有上述的 Node root
class Tree{
    public Node root;
}


public class Test {
    public static Node createTree(){
        // 简单粗暴
        // 先创建出所有的节点
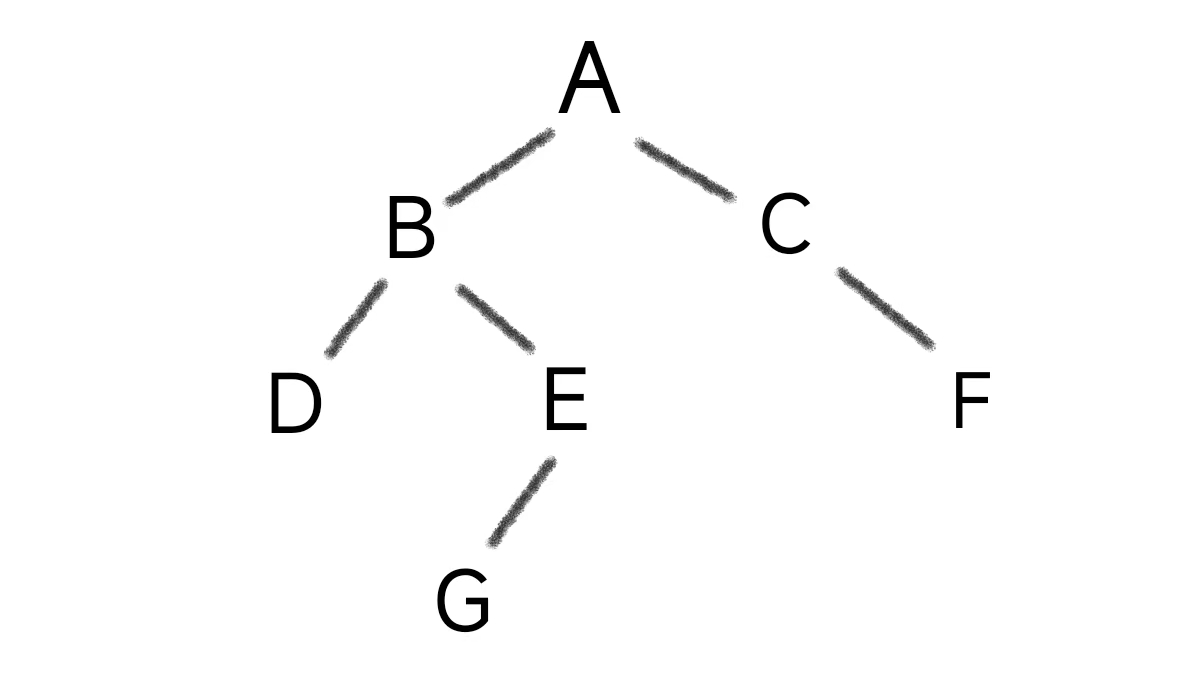
        Node a = new Node("A");
        Node b = new Node("B");
        Node c = new Node("C");
        Node d = new Node("D");
        Node e = new Node("E");
        Node f = new Node("F");
        Node g = new Node("G");

        // 把这些节点（引用赋值）连起来
        a.left = b;
        a.right = c;
        b.left = d;
        b.right = e;
        c.right = f;
        e.left = g;

        return a;
    }
    // root 表示一棵树
    //Node root = new Node("A");

    // 也可以表示一个树， 日常工作更常见
    //Tree tree = new Tree();

初一十五的月亮天天变的不一样原来所谓地久天长也只是误会一场

那首歌我慢慢唱你问我爱你有多深我爱你有几分

—— 月亮代表谁的心 DT

🌟💗🦀