【定理】算术基本定理（唯一分解定理）

大蒟蒻来水贴了！

算术基本定理（唯一分解定理）

一句话：
　　　　
任何大于１的自然数，都可以唯一分解成有限个质数的乘积

例如对于大于1的自然数n，

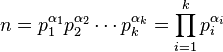
这里P$_i$均为质数，其指数a$_i$是正整数。
这样的分解称为的标准分解式。

---

唯一分解定理具有：
　①唯一性（分配方式的唯一性）
　②存在性　　　　

---

证明：

百度百科+自己胡搞了+自己以前做的笔记

①唯一性
　　首先明确一个事实，若p是ab的约数（p|ab,p可以整除ab），则p不是a的约数，就是b的约数。
　　如果p是a的约数则证毕。如果p不是a的约数，则p和a的最大公约数为1。
　　则由裴蜀定理推得，因为使a,b互质的充要条件是存在整数x,y使ax+by=1。
　　于是b=b(ma+np) =abm+bnp（……）；
　　因为先前已经知道p是ab的约数，则上式右边两项都可以被p整除。
　　所以p就是b的约数。
　　唯一性得证。
　　
②存在性
　　假设n为不能被分为质数的乘积的自然数之一，切n为最小
　　因为设n为大于1的合数（如果n为质数，则只有n=n，显然这是质数的乘积）
　　因为每个合数都可以分为两个大于1小于它的两自然数的乘积
　　所以n=a×b
　　又因为n为不能被分为质数的乘积的自然数中最小的一个
　　所以a和b可以分为质数的乘积
　　所以n已就可以分为质数的乘积，与假设不符合，故假设错误
　　存在性得证。　

---

　　现在我们来看下下下面这个式子：
　　已知gcd[最小公约数] (a,b)，lcm[最大公倍数] (a,b)；
　　a×b=gcd(a,b)×lcm(a,b)
　　
　　a=12;b=14
　　gcd(a,b)=2 ; lcm(a,b)=84 ;
　　tot=168 [gcd(a,b)×lcm(a,b)]
　　a×b＝12×14=168
　　然后
　　12=3×4
　　14=2×7
　　：
　　：
　　12=2^1×2^1×3^1
　　14=2^1×7^1
　　所以 max=7^1×3^1×=21
　　　　 min=2^1×2^1×2^1=8
　　　　 min×max＝168 = gcd(a,b)×lcm(a,b) = a×b
　　
　　所以gcd(a,b)×lcm(a,b) = a×b
　　
　　证明：
　　设x=gcd(a,b)，y=lcm(a,b)
　　则a=m×x，b=n×x,m与n互质
　　故y=m×n*x
　　因此x×y=x×(m×n×x)=(m×x)×(n×x)=a×b
　　即a×b=gcd(a,b)×lcm(a,b)

---

THE END

Ｔｈａｎｋ ｙｏｕ　ｆｏｒ　ｗａｔｃｈｉｎｇ