矩形中数方格

题目描述

余姚市要新建一个广场，为了美观，要求完全是正方形。目前正在规划当中，正方形的大小和位置都在热烈的讨论之中。假设将可用于造广场的区域看成一个矩形，由1*1的单位正方形构成。如下图：这是一个4*6的矩形区域。 

广场要求必须在这个矩形范围内，广场边线不能跨过任意一个单位正方形内部，只能与正方形边线重合，且广场必须为正方形。那么上图中，以下4种正方形均为可行方案： 

 

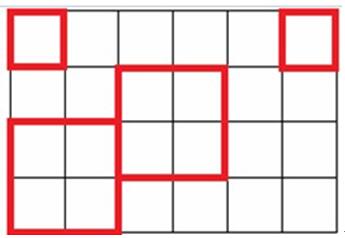
市民们提出了很多建造广场的方案。现在领导想要知道，到底有多少种不同的方案可以选择？请你设计一个程序，来计算以下建造广场的最多可行方案数。

输入

第一行两个整数n和m（1<=n,m<=1000），表示用于建造广场区域的长和宽。

输出

一个整数，建造广场的可行方案数。

样例输入 

1 5

样例输出 

5

这题我查了半天感觉其他人写的代码好长（小白表示看不懂）

本意就是一个由n*m单位正方形组成的矩形求里面有多少个正方形。

查了半天找了个公式：n*m+(n-1)*(m-1)+(n-2)(m-2)*......一直到这俩有一个减成0了为止。

得到的就是正方形的个数。

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <string>
#include<cmath>
#include<iomanip>
#include<cstdlib>
#include<ctime>
#include<algorithm>
#include<stdio.h>
#include<cstdio>
#include<cstring>
#include<map>
#define M 100000
using namespace std;
int main()
{
    
    int n, m,s=0;
    cin >> n >> m;
    int a, b, c;
    a = n;
    b = m;
    while (a != 0 && b != 0)
    {
        c = a * b;
        s = s + c;
        a--;
        b--;
    }
    cout << s;

    return 0;
}