机器学习 - SVD分解算法的物理意义

机器学习-SVD分解算法的物理意义

奇异值分解（Singular Value Decomposition），以下简称SVD。

奇异值分解算法是一种在机器学习中经常使用到的一个算法，SVD主要用于数据压缩和数据降维，在图像压缩、推荐系统有着极其重要的作用，

本文将着重理解SVD分解算法的物理意义以及我们将用Python代码将这个过程可视化，数学推导将不是本文的重点，将在它文展示。

一.SVD分解介绍

任何一个形状的矩阵（图像）都可以转化从先旋转、再延伸、再旋转的形式。

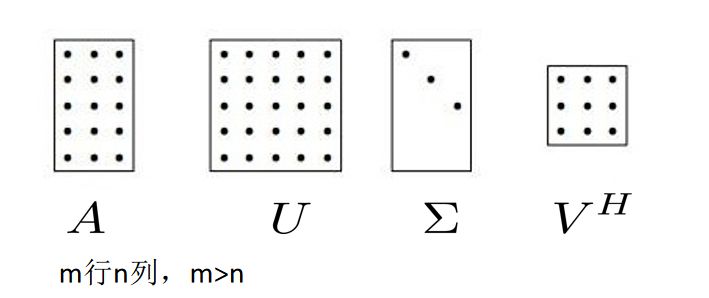
公式如下

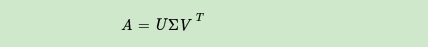
SVD分解就是将一个矩阵转变为这三个矩阵的表达形式，同时，这三个矩阵分别代表一个旋转、一个伸缩、一个旋转。

为什么呢？

提出问题就解决了一半的问题。为什么一个矩阵可以转变为一个旋转矩阵、一个伸缩矩阵、一个旋转矩阵相乘呢？

让我们来看一个简单的例子

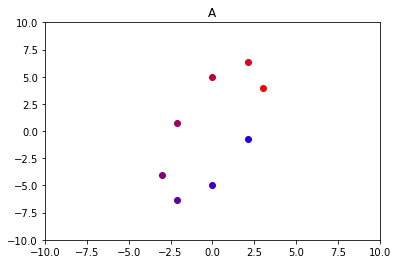
Unit circle 要怎么转换才能转换成为下图中的A的形式呢？（这里要注意点的颜色！）

首先，我们先让Unit circle逆时针旋转135度。

再让旋转后的图像在x轴上伸长6.70820393249937倍（为什么是这个倍数，先不用纠结，这是奇异值分解以后的一个奇异值数），在y轴上伸长2.2360679774997894倍

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4t8jcxUO-1652606694313)(https://s1.328888.xyz/2022/05/15/qmJhX.png)]

然后我们再让图像旋转一次，即可得到和A同等的一个图像. U sigma Vt

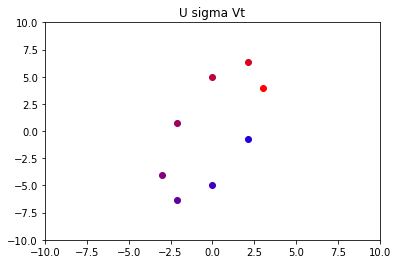
这样，原图到A的过程就可以转变为将原图先进行一个旋转、再进行一个伸缩、再进行一个旋转。

我们知道，任何的图像的变化都可以用线性代数里的一个矩阵来表示。

实际上，从原图到A的一个变换矩阵就是

$$A=\left|\begin{array}{cc}3& 0\\ 4& 5\end{array}\right|$$

我们将其拆解以后，第一个转换图像对应的旋转是逆时针旋转135度，我们可以将第一个旋转用矩阵表示为

$$V=\left|\begin{array}{cc}-0.71& -0.71\\ -0.71& 0.71\end{array}\right|$$

然后进行左乘一个伸缩矩阵（注意里面的数字和上面那个伸缩大小之间）

$$\Sigma =\left|\begin{array}{cc}6.71& 0\\ 0& 2.24\end{array}\right|$$

然后最后再左乘一个旋转矩阵

$$U=\left|\begin{array}{cc}-0.32& -0.95\\ -0.95& 0.32\end{array}\right|$$

我们用Python中的Nupmy来协助我们计算一下这三个矩阵相乘后是否等于A

import numpy as np

V =np.array( [[-0.71 ,-0.71],
 [-0.71 , 0.71]])

sigma = np.array([[6.71 ,0.  ],
 [0.  , 2.24]])

U = np.array([[-0.32 ,-0.95],
 [-0.95  ,0.32]])

res1 = np.matmul(U, sigma)
res1
res2 = np.matmul(res1,V)
res2

array([[3.035392, 0.013632],
       [4.016967, 5.034823]])

我们看到矩阵相乘后生成了一个新的矩阵，而这个矩阵正是和A矩阵极其相近的一个矩阵（计算机已经认为一致）

$$res2=\left|\begin{array}{cc}3.035392& 0.013632\\ 4.016967& 5.034823\end{array}\right|$$

$$A=\left|\begin{array}{cc}3& 0\\ 4& 5\end{array}\right|$$

现在我们已经可以将一个复杂的变化（或者称之为一个复杂的变化矩阵）转变为三个简易的变化（或者称之为三个简易的变化矩阵）相乘（一个旋转、一个伸缩、一个旋转），然而事实上，任何一个复杂的变化都可以转变为这种分解的形式（在这里我们用二维矩阵来表示，为的是得到一个可视化的变化）我们称之为SVD奇异值分解。

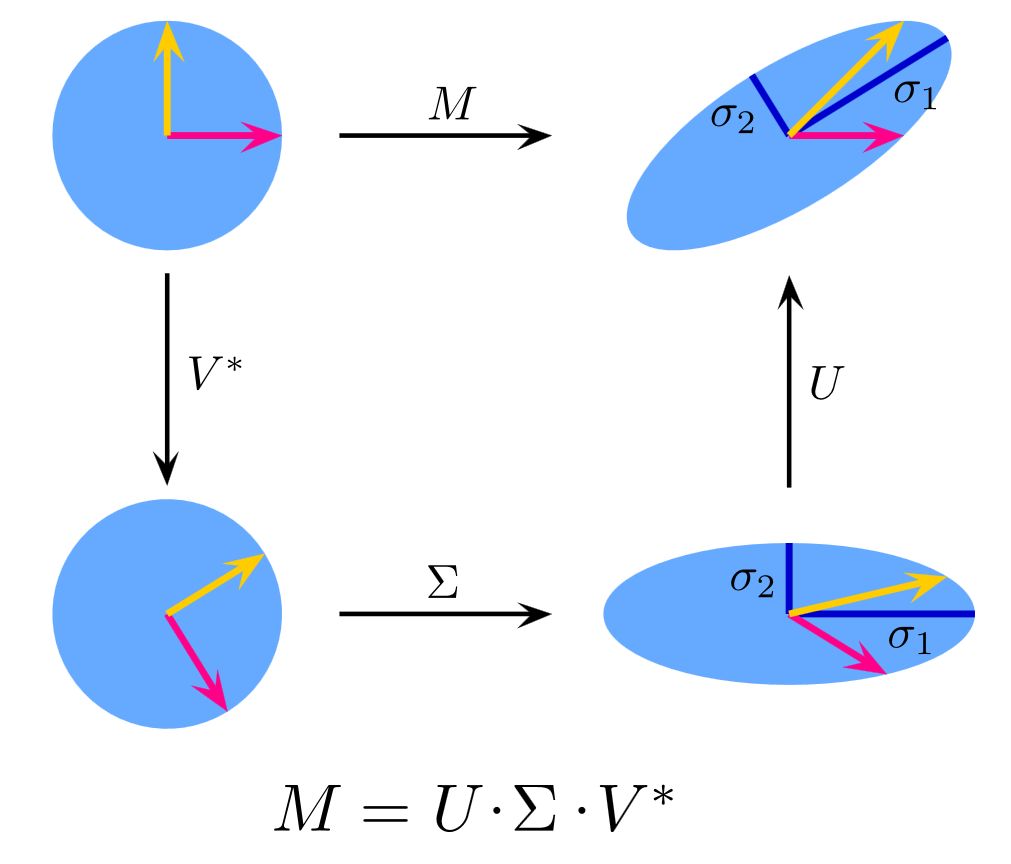
你也看到了，$\Sigma$是一个特殊的对角矩阵，而且通过刚刚可视化的转化，你知道$\Sigma$内对角线上面的数字代表了对矩阵的变化大小程度（对拉伸变化的大小程度）也就是说$\Sigma$内对角元素更像是代表了一种权重，比如我们将x轴拉伸为原来的6.71倍，这个变化看起来相较于将y轴变为原来的2.24倍大一点，说明我们在x轴上面进行的操作特征更接近于与原矩阵进行的操作，实际上$\Sigma$内对角线的元素从大到小排列，我们通常只需要取出前面的几个特征值就能很好的将原图像的图像表示出来，这同时也与图像压缩相关，因为计算机内的图像实际上是数以百万计的矩阵像素形式。

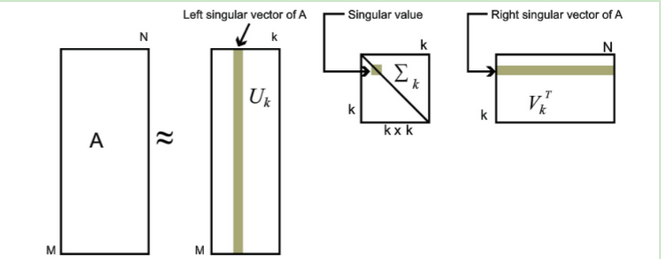
由于$\Sigma$是一个对角矩阵，即对角线上面存在元素，而其他位置的元素为0，根据矩阵相乘的原理，我们可以将$\Sigma$内的对角元素提取出来，这个公式就转换成了

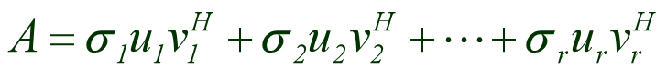
其中$\sigma 1$代表$\Sigma$中的第一个对角元素，u1代表U矩阵中的第一行，v1转置代表V矩阵中的第一列

刚刚那个矩阵由于奇异值都相差不是很大，所以说“$\Sigma$内的对角元素更多代表一种和原图像相似的一个权重”展示的可能不是那么明显。

如果我们将x轴延申80倍，然后y轴转换为原图的2倍看一看

图像就变为了这样的：

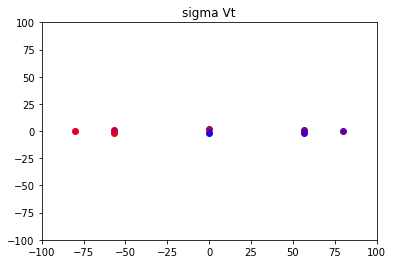
最终的结果：

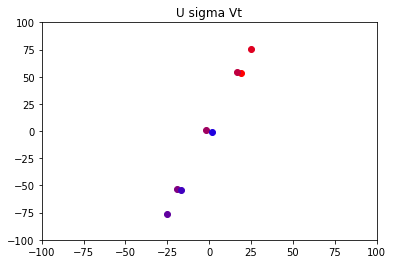
该图像对应原图的的变换矩阵为：

$$A=\left|\begin{array}{cc}19.23018461& 16.54690303\\ 53.21841786& 54.11284506\end{array}\right|$$

这样看来，似乎对y轴的操作看起来微乎其微，因为这些不同颜色的点已经几近贴合为一条线，那如果我们直接舍去对y轴的操作，

图像变为了这样：

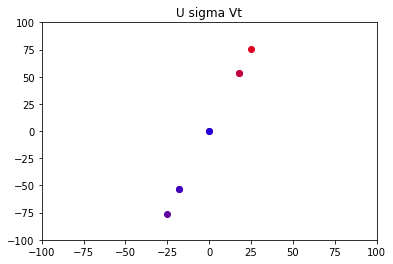
我们来看看该图像对应的变换矩阵为：

$$\sigma 1\mu 1v1=B=\left|\begin{array}{cc}17.88854382& 17.88854382\\ 53.66563146& 53.66563146\end{array}\right|$$

B和A极其相似！

也就是说我们现在只保留最大的那个特征值，相乘后的结果与原图差别并不是很大，即该矩阵结果与原来的矩阵相差不是很大，很好的拟合了原矩阵的图像。

但我们依然来看看如果将第一个特征值抹去为0，只保留第二个奇异值来计算矩阵的大小C为多少？，由于矩阵相乘原理，其他地方置为0，保留第二个奇异值计算相当于将第二个奇异值乘以V的第二行然后乘以U的第二列。

在100x100的视窗里面，它似乎成了一个点，而且没有怎么动，与U sigma Vt的图像从视觉上看相差很大，而且C的结果也很小，与A矩阵相差很大（在这里C实际上就是A-B的结果）

$$\sigma 2\mu 2v2=C=\left|\begin{array}{cc}1.34164079& -1.34164079\\ -0.4472136& 0.4472136\end{array}\right|$$

所以，现在你应该能够更能理解奇异值的大小更多的代表一种相似权重这个意思吧。SVD分解将$\Sigma$的“头部”集中了更多的“质量”，忽略远离“头部”的奇异值对恢复矩阵的影响越小,也就是说我们在上面这个例子里面，只拿出第一个$\Sigma$的值就能很好的相似拟合出原来A的矩阵，而可以舍去其他奇异值，因为它们对整个矩阵A的拟合影响不是很大，无论是从这个二维画图来看，还是从矩阵内的的数字大小来看都可以看出来。

如何用Python中的Numpy计算SVD？

Python中有一个Numpy库中，已经给我们内置了一个函数svd(matrix)可以直接求出一个矩阵的SVD分解后的U、$\Sigma$、V

import numpy as np
from numpy.linalg import svd
P = np.array([[3,1,4,1],[5,9,2,6],[5,3,5,8],[9,7,9,3]])
U,S,V=svd(P)
U

array([[-0.21472623,  0.37397651, -0.13150279, -0.89260362],
       [-0.5186023 , -0.70137666,  0.43020321, -0.23248147],
       [-0.48143993, -0.20822528, -0.83770916,  0.15199076],
       [-0.67317152,  0.56996016,  0.30963782,  0.35511962]])

S

array([21.23135684,  6.43244475,  4.88175527,  0.14699287])

V

array([[-0.55120987, -0.51992284, -0.48804478, -0.43319766],
       [ 0.26483885, -0.40006067,  0.65008996, -0.58923246],
       [ 0.07265877,  0.69537763, -0.21865293, -0.68070665],
       [ 0.78787611, -0.29339674, -0.53980203, -0.04222983]])

可以看到，在使用Numpy进行SVD计算时，对角矩阵$\Sigma$转化为了一个向量形式S的表达形式，如果要转化为矩阵形式，可以使用np.diag(S)函数进行转化

sigma1 = np.diag(S)
sigma1

array([[21.23135684,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  6.43244475,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  4.88175527,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.14699287]])

奇异值包含了矩阵的“本质信息”

仔细看一看B矩阵，你能发现什么？

$$B=\left|\begin{array}{cc}17.88854382& 17.88854382\\ 53.66563146& 53.66563146\end{array}\right|$$

没错，B是一个Rank为1的矩阵，实际上，当我们将每一项奇异值取出相乘再相加时，我们就是将多个Rank为1的矩阵相加

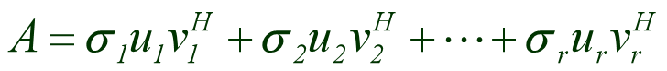
为什么说奇异值包含了矩阵的“本质信息”呢？

你看，如果一个矩阵“足够奇异”，那么我就只需要取出前几项奇异值对应的rank为1的矩阵相加就能很好的拟合出原矩阵，奇异值能够剖析矩阵的本质，深析这个原矩阵是个多少Rank的一个矩阵，也就是说矩阵越“奇异”，其行（或列）向量彼此越线性相关，越能彼此互相解释。即奇异值包含了矩阵的“本质信息”

这里也能间接告诉我们一个信息，那就是$\Sigma$ 内有多少个奇异值，原来的矩阵就是Rank为几的一个矩阵。

在图像压缩上面的应用

我们将尝试将这个爱心进行图像压缩

这里需要提一下的是，我们都知道在电脑中一个图像就是由许多像素点组成的一个矩阵，所以上图的矩阵我们可以表达为

D = np.array([[0,1,1,0,1,1,0],
              [1,1,1,1,1,1,1],
              [1,1,1,1,1,1,1],
              [0,1,1,1,1,1,0],
              [0,0,1,1,1,0,0],
              [0,0,0,1,0,0,0],
             ])

0代表白色区域，1代表黑色区域

我们先利用Numpy中的svd函数将矩阵D的U,S,V值求出

U,S,V=svd(D)
print(np.round(U,2))
print()
sigma = np.diag(S)
print(np.round(sigma,2))
print()
print(np.round(V,2))

[[-0.36  0.   -0.73 -0.05  0.33  0.48]
 [-0.54 -0.35  0.27 -0.08 -0.58  0.4 ]
 [-0.54 -0.35  0.27 -0.08  0.58 -0.4 ]
 [-0.45  0.35 -0.27  0.52 -0.33 -0.48]
 [-0.28  0.71  0.18 -0.62 -0.   -0.  ]
 [-0.08  0.35  0.46  0.57  0.33  0.48]]

[[4.74 0.   0.   0.   0.   0.  ]
 [0.   1.41 0.   0.   0.   0.  ]
 [0.   0.   1.41 0.   0.   0.  ]
 [0.   0.   0.   0.73 0.   0.  ]
 [0.   0.   0.   0.   0.   0.  ]
 [0.   0.   0.   0.   0.   0.  ]]

[[-0.23 -0.4  -0.46 -0.4  -0.46 -0.4  -0.23]
 [-0.5  -0.25  0.25  0.5   0.25 -0.25 -0.5 ]
 [ 0.39 -0.32 -0.19  0.65 -0.19 -0.32  0.39]
 [-0.22  0.42 -0.44  0.42 -0.44  0.42 -0.22]
 [ 0.55 -0.44  0.09  0.   -0.09  0.44 -0.55]
 [-0.4  -0.55 -0.2  -0.    0.2   0.55  0.4 ]
 [ 0.2   0.1  -0.67  0.    0.67 -0.1  -0.2 ]]

我们将$\Sigma$中的第一个值4.74取出，计算这个rank1的矩阵

$$\sigma 1\mu 1v1$$

t = S[0]*np.outer(U[:,0],V[0])
print(np.round(t,2))

[[0.39 0.68 0.78 0.68 0.78 0.68 0.39]
 [0.59 1.02 1.17 1.02 1.17 1.02 0.59]
 [0.59 1.02 1.17 1.02 1.17 1.02 0.59]
 [0.48 0.84 0.97 0.84 0.97 0.84 0.48]
 [0.3  0.52 0.6  0.52 0.6  0.52 0.3 ]
 [0.09 0.16 0.18 0.16 0.18 0.16 0.09]]

取第二个奇异值1.41，计算出$$\sigma 2\mu 2v2$$，取第三个奇异值1.41，计算出$$\sigma 3\mu 3v3$$…我们看到奇异值非0数只有4个，说明原矩阵是一个rank为4的矩阵，当我们取到第四个奇异值$$\sigma 4\mu 4v4$$将再将这些所有的秩一矩阵相加即可还原原矩阵D的图像

t = S[1]*np.outer(U[:,1],V[1])
print(np.round(t,2))

[[-0.   -0.    0.    0.    0.   -0.   -0.  ]
 [ 0.25  0.13 -0.13 -0.25 -0.13  0.13  0.25]
 [ 0.25  0.13 -0.13 -0.25 -0.13  0.13  0.25]
 [-0.25 -0.13  0.13  0.25  0.13 -0.13 -0.25]
 [-0.5  -0.25  0.25  0.5   0.25 -0.25 -0.5 ]
 [-0.25 -0.12  0.13  0.25  0.13 -0.12 -0.25]]

t = S[2]*np.outer(U[:,2],V[2])
print(np.round(t,2))

[[-0.4   0.33  0.2  -0.67  0.2   0.33 -0.4 ]
 [ 0.15 -0.12 -0.07  0.25 -0.07 -0.12  0.15]
 [ 0.15 -0.12 -0.07  0.25 -0.07 -0.12  0.15]
 [-0.15  0.12  0.07 -0.25  0.07  0.12 -0.15]
 [ 0.1  -0.08 -0.05  0.17 -0.05 -0.08  0.1 ]
 [ 0.25 -0.21 -0.12  0.42 -0.12 -0.21  0.25]]

t = S[3]*np.outer(U[:,3],V[3])
print(np.round(t,2))

[[ 0.01 -0.02  0.02 -0.02  0.02 -0.02  0.01]
 [ 0.01 -0.02  0.03 -0.02  0.03 -0.02  0.01]
 [ 0.01 -0.02  0.03 -0.02  0.03 -0.02  0.01]
 [-0.08  0.16 -0.17  0.16 -0.17  0.16 -0.08]
 [ 0.1  -0.19  0.2  -0.19  0.2  -0.19  0.1 ]
 [-0.09  0.17 -0.18  0.17 -0.18  0.17 -0.09]]

我们看到，在$$\sigma 4\mu 4v4$$时，这个矩阵内的数字大小已经很小，几近为0了。

在算$$\sigma 5\mu 5v5$$时，由于奇异值$\sigma 5$以及为0，所以该$$\sigma 5\mu 5v5$$以及为一个零矩阵

t = S[4]*np.outer(U[:,4],V[4])
print(np.round(t,2))

[[ 0. -0.  0.  0. -0.  0. -0.]
 [-0.  0. -0. -0.  0. -0.  0.]
 [ 0. -0.  0.  0. -0.  0. -0.]
 [-0.  0. -0. -0.  0. -0.  0.]
 [-0.  0. -0. -0.  0. -0.  0.]
 [ 0. -0.  0.  0. -0.  0. -0.]]

我们计算可以得出
$$result=D=\sigma \mu 1v1+\sigma 2\mu 2v2+\sigma 3\mu 3v3+\sigma 4\mu 4v4$$

我们来看看$$\sigma x\mu xvx$$

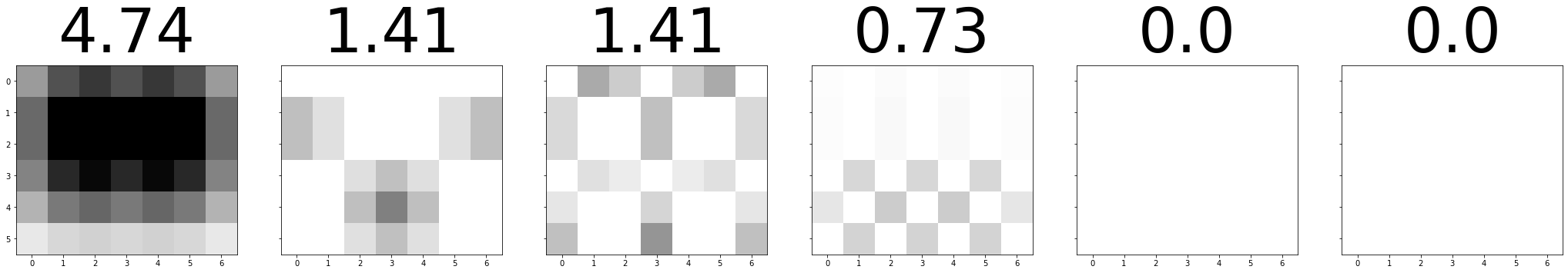
将每一个秩1矩阵相加起来的图像

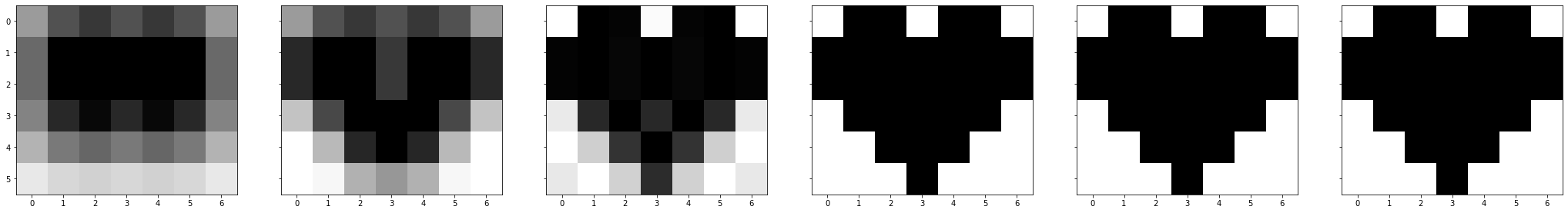
可以清晰看到，加到第四个矩阵时，我们就已经得到与原图像（原矩阵）一模一样的图像（矩阵）

这个图像比较小，8x8图像，该图像可能无法让你感觉到奇异值的重要性。

但如果说我们的矩阵是一个1000x1000的图像（一般电脑的图片比这个还要大），如果我们要记录这个图片，我们原本需要电脑记录1000x1000=1000000个像素！也就说一张照片我们需要存入一百万个值。

但如果我们用到了SVD分解，将图片转化为4个秩1的矩阵相加的情况，我们只需要保留2000x4=8000个像素就能完全呈现一个一模一样的原图。

如果我们准备将图片压缩，我们可以舍去后两个秩1矩阵，因为我们之前已经说了$\Sigma$头部的值往往代表了这个图片的“本质信息”，那就只需要保留2000x2=4000个像素数据就能差不多拟合出原图的照片。

但往往很多时候我们交给计算机处理视觉问题时并不需要一个清晰度极其高的一张图片，这和人类的视觉系统类似。

比如给你这样一张图片

(希望没有吓到你)

虽然很模糊，但你还是知道它是一只狗。

所以让计算机去处理这些视觉问题时，我们往往只要勾勒出原图的一个模糊图像，能够近似拟合原图的一个图像就行了，这就与SVD分解息息相关。

当然，SVD的应用远不止如此，SVD在图像恢复、PCA、异常检测、图像去噪、推荐系统、SLAM都有着巨大的作用。

感兴趣的话可以去搜一搜，关于SVD分解的数学讲解将放在下一章。