TOJ 1545

最新推荐文章于 2021-01-14 11:24:30 发布

Laimic_

最新推荐文章于 2021-01-14 11:24:30 发布

阅读量468

点赞数

分类专栏： ACM解题报告文章标签：动态规划

本文链接：https://blog.csdn.net/laimic_/article/details/17244989

版权

ACM解题报告专栏收录该内容

29 篇文章 0 订阅

订阅专栏

题目连接:

http://acm.tzc.edu.cn/acmhome/problemdetail.do?&method=showdetail&id=1545

题目类型:

动态规划 - 阶段决策

数据结构:

struct LMIC_PROCE
{
	int T1, T2, T3, F1, F2;
} * proce;

// 第 i 个阶段, 剩余容量 j;
int dmic[1200][1200] = { -1 };

思路分析:

------------------------------------------------------------------------

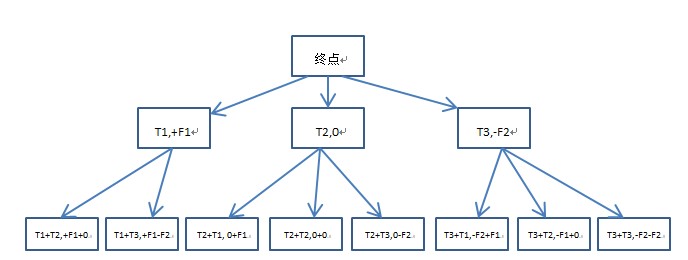
动态规划 : 自顶向下 + 备忘录

从终点开始往回搜索

每个阶段可以进行选择.

如果剩余力气大于F1

则可以进行 T1, T2, T3 选择

否则,只能进行 T2,T3 选择

源代码:

#include <stdio.h>
#include <string>
#include <iostream>
using namespace std;

struct LMIC_PROCE
{
	int T1, T2, T3, F1, F2;
} * proce;

// 第 i 个阶段, 剩余容量 j;
int c, dmic[1200][1200] = { -1 };
int n, m;

int _min( int a, int b )
{
	return a < b ? a : b;
}
int _min( int a, int b, int c )
{
	int tmp = 1000;

	if( a < tmp ) tmp = a;
	if( b < tmp ) tmp = b;
	if( c < tmp ) tmp = c;

	return tmp;
}

int _dmic( int n, int f )
{
	if( n < 1 )
	{
		dmic[n][f] = 0;
		return dmic[n][f];
	}

	if( dmic[n][f] != -1 )
	{
		return dmic[n][f];
	}

	if( f >= proce[n - 1].F1 )
	{
		int left = _dmic( n - 1, f - proce[n - 1].F1 ) + proce[n - 1].T1;
		int middle = _dmic( n - 1, f ) + proce[n - 1].T2;
		int right = _dmic( n - 1, f + proce[n - 1].F2 >= m ? m : f + proce[n - 1].F2 ) + proce[n - 1].T3;

		dmic[n][f] = _min( left, middle, right );

		return dmic[n][f];
	}
	else
	{
		int left = _dmic( n - 1, f ) + proce[n - 1].T2;
		int right = _dmic( n - 1, f + proce[n - 1].F2 >= m ? m : f + proce[n - 1].F2 ) + proce[n - 1].T3;

		dmic[n][f] = _min( left, right );

		return dmic[n][f];
	}
}

int main()
{
	int i, t;

	scanf( "%d", &t );

	while( t -- )
	{
		memset( dmic, -1, sizeof( dmic ) );

		scanf( "%d%d", &n, &m );

		proce = new LMIC_PROCE[ n + 1 ];

		for( i = 0; i < n; i ++ )
		{
			scanf( "%d%d%d%d%d", &proce[i].T1, &proce[i].T2, &proce[i].T3, &proce[i].F1, &proce[i].F2 );
		}

		printf( "%d\n", _dmic( n, m ) );

	}

	return 0;
}