题目
在遥远的西方有一个古老的王国,国王将他的王国分成了网格状,每一块称之为一个城市。在国王临死前,他将这些城市分给了自己的N个儿子(编号为0到N-1)。然而这N个王子的关系不是很好,0讨厌1,1讨厌2,2讨厌3……N-1讨厌0。
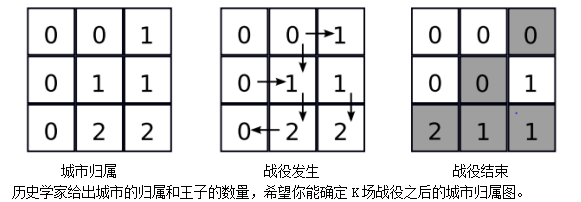
在国王死后,这种不好的关系使得王子之间爆发了战争。战斗只会在相邻的两个城市之间爆发(共有一条边称之为相邻),并且只有当A讨厌B时,A才会对B发起战斗,结果必定是A获得这次战斗的胜利。当一方胜利后,他所进攻的城市就会变成进攻方的。许多战斗是同时发生的,我们称之为一场战役。当多场战役发生之后,剩下的王子将不再发生战争。
例如,如果有3个王子,那么战斗过程如下所示:
样例输入:
第一行输入4个数,N,R,C,K。有N个王子,王国分为R*C的网格图。询问K场战役之后的城市归属图。
下面R行,每行C个数字,表示一开始城市的归属。
3 4 4 3
0 1 2 0
1 0 2 0
0 1 2 0
0 1 2 2
样例输出:
2 2 2 0
2 1 0 1
2 2 2 0
0 2 0 0
数据范围:
2<=N<=100
2<=R,C<=100
1<=K<=100
保证数据合法.
思路
暴力。。。。。。。
解法
暴力。。。。。。
代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#define fo(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int maxn=105;
int f[maxn][maxn],g[maxn][maxn],n,r,c,kk;
int way1[4]={1,-1,0,0},way2[4]={0,0,1,-1};
int main()
{
// freopen("T.in","r",stdin);
scanf("%d%d%d%d",&n,&r,&c,&kk);
fo(i,1,r)
fo(j,1,c) {
scanf("%d",&g[i][j]);
f[i][j]=g[i][j];
}
fo(pp,1,kk){
fo(i,1,r){
fo(j,1,c){
fo(k,0,3){
int nx=i+way1[k],ny=j+way2[k];
if (nx<1||nx>r||ny<1||ny>c) continue;
if (((g[i][j]+1)%n)==g[nx][ny])
f[nx][ny]=g[i][j];
}
}
}
memcpy(g,f,sizeof(f));
}
fo(i,1,r){
fo(j,1,c) printf("%d ",f[i][j]);
printf("\n");
}
}


























 1432
1432

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








