回溯算法：深度优先搜索的终极指南

概念：

• 回溯算法本质上是一种深度优先搜索（DFS）算法，它在搜索过程中尝试所有可能的路径来找到问题的解。
• 它通过不断地选择不同的分支进行探索，当发现当前分支无法得到可行解或最优解时，就 “回溯” 到上一个状态，尝试其他分支，直到找到所有解或确定无解。

学习路线：

在掌握回溯算法之前，我们先学习递归和搜索

可以这样看递归是一个集合，里面有搜索，搜索里面又在加一点东西形成回溯

层层递进的学习，会在后面学习回溯算法很轻松

消除递归的恐惧

 

我们在学习c语言c++数据结构时，已经简单的见过和使用过递归，无非就是函数自己调用自己

但前期的学习需要花很多图去表示递归调用过程或者画栈的示意图

这里我们将深入了解递归 ：函数自己调用自己

关于二叉树的遍历：这里讲解后序遍历，左右根，当我们遍历一个结点时，先考虑左子树，右子树，根，遍历左子树时，又把左子树看成根节点，在左右根，依次递归下去

此时你就会发现，遍历每一个结点时都是左右根，都是相同的问题

 

我们在研究主问题时，发现子问题也是相同的，如果设解决主问题需要用到函数f，解决相同的子问题也会用到f，因为他们是相同的问题，此时就会出现f调用f的情况，就是函数自己调用自己 

深刻理解为什么会用到递归？？？

本质就是研究一个问题时又碰到相同的子问题，而且方法一样，就必然会出现函数自己调用自己 

 

第一层：需要掌握递归展开的细节图（这里默认大家都会）

第二层：做过很多二叉树的题目（这里默认大家都做过）

第三层：宏观看待递归的过程（在掌握前两层的基础上，大家可能对二叉树的题目会做，但是换到别的题目就可能不会了，这也就为什么要讲第三层）

第三层中 ：1.不要在意递归的细节展开图（可能画的草稿纸都不够）

                   2.把递归的函数当成一个黑盒（只要想这个黑盒能返回你想要的结果即可，不要去想完成的过程）

                  3.相信这个黑盒一定能完成这个任务

感性理解第三层：以二叉树后序遍历讲解

 

把函数dfs想象成一个黑盒，它能返回你想要的结果

那就是dfs我传一个根结点，它就会帮我遍历后序

dfs如何完成后序遍历？（首先你要相信它能够完成）

是不是先后序遍历左子树，在后序遍历右子树，最后遍历自己

dfs是不是完成后序遍历，所以就dfs（root->left）；dfs（root->right）

 

注意再写递归代码的时候，是不是不能写成死递归，所以要有一个出口

出口就是分成的子问题不能再分了，就是你调用到最底下不能在调用的时候，

那不就是当遍历的叶子结点的时候就不需要调用了吗

那就if（root==null）return；即可 

1.我们得找到相同的子问题，这关乎函数头怎么设计

为什么你在后序遍历时传入一个根节点就行？？？

原因在于你发现子问题是给一个根节点，然后完成后序遍历

在归并那里，就是一个数组，然后标记一下数组的左边和右边，完成数组的排序

2.只关心某一个子问题如何解决（相信黑盒能完成）

3.避免写死递归（只需关心子问题不能分隔的时候，二叉树就是叶子结点，归并就是区间有效）

理解搜索： 

 

以二叉树的遍历为例：

深度优先遍历：先往下走在往上

宽度优先遍历：一层一层的遍历

那什么是搜索呢？？？ 

搜索是搜索里面的某一个值

可以这样说深度优先遍历和深度优先搜索一样

遍历是一种形式，目的是搜索

DFS 是 “Depth - First Search” 的缩写，中文是 “深度优先搜索”。BFS 是 “Breadth - First Search” 的缩写，中文是 “广度/宽度优先搜索”。（后面的学习用英文缩写）

搜索：就是把所有的情况枚举一遍：看你使用的是dfs还是bfs罢了

本次的讲解以dfs为例讲解，不讲bfs（bfs适合走迷宫），这里我们全用递归的方法，当然是dfs 

（不是bfs不能解决，你可以用队列把每一层记录下来）

 

第一点：不要认为只有图和二叉树这种经典的才能用深度优先搜索

第二点对于全排列，比如1/2/3进行全排列，我们要想到初高中学的树状图

这里是根据第一个格子填什么，第二个填什么，到最后出结果（这种可以叫决策树）

那这里我们就可以用深度优先搜索，暴力穷举所有的可能性

 

这是高中的树状图（脑海里可以想象） 

理解回溯：

回溯的本质就是深搜，两个概念可以认为一样，在看题解的时候会发现有人用回溯有人用深搜

本质是一样的

以走迷宫为例：每走到一个拐点，都可以分左右，那我第一个往左走，发现行不通，就回到上一级的这个操作就称之为回溯，然后在由上一级往另一边走

（也就是回退上一级的这个操作称之为回溯）

所以深搜一定带回溯（你可以把他们认为同一个东西）

什么是剪枝？？？

在迷宫里如果发现一条路走不通就剪掉

这就像树中，这个不要不选，就剪掉，就是我们在遍历决策树时，发现不是我们要的结果就剪掉 

 

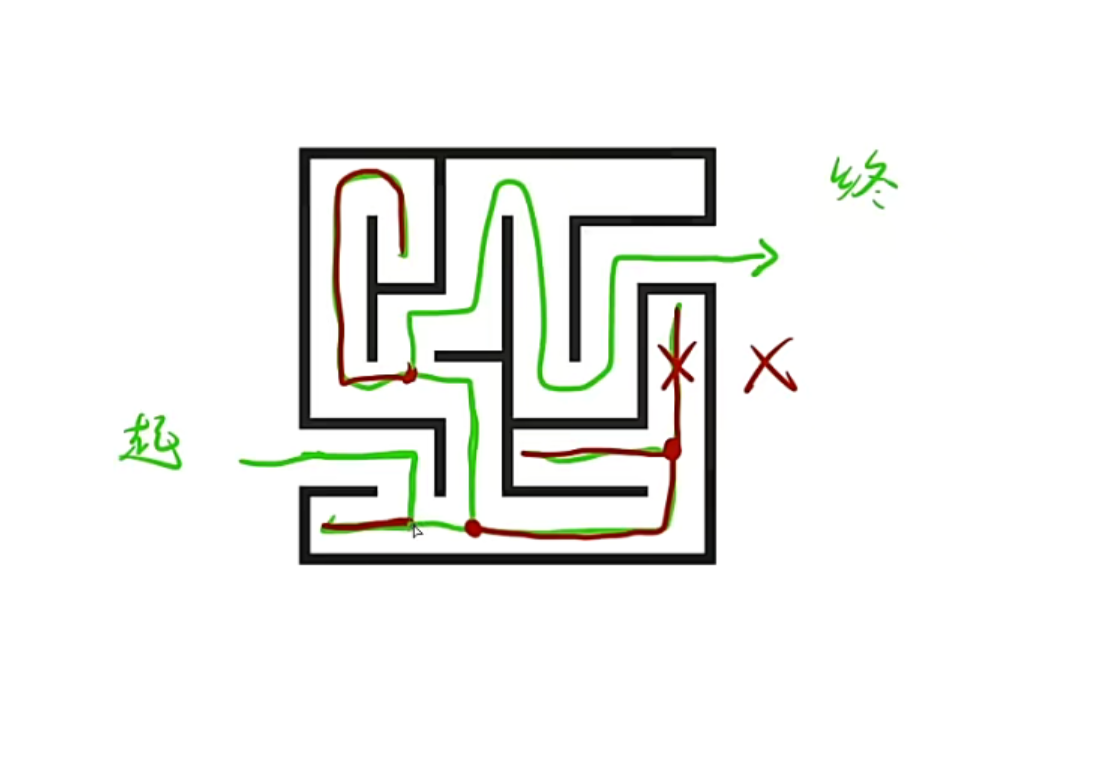
用红色表示回溯（回退上一级）

 

总结：回溯就是dfs，我们学习回溯就要学dfs，学习dfs又要理解递归

所以我们先进行递归的学习->dfs->回溯->综合练习