矩阵快速幂

最新推荐文章于 2021-05-19 22:27:29 发布

无糖卡布奇诺

最新推荐文章于 2021-05-19 22:27:29 发布

阅读量428

点赞数 5

分类专栏：知识点整理

本文链接：https://blog.csdn.net/LeBron_Yang/article/details/82935245

版权

知识点整理专栏收录该内容

5 篇文章 2 订阅

订阅专栏

矩阵快速幂，可用于一些dp的优化，比如斐波那契的递推式等的优化，可将递推式转化成矩阵相乘，从而变成矩阵乘矩阵的n次方，再通过，快速幂算法，即可完成优化，以斐波那契递推式进行举例；

第一步，是求出递推式，即f(n)=f(n-1)+f(n-2)

第二步，构造矩阵

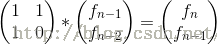简写成T * A(n-1)=A(n)，T矩阵就是那个2*2的常数矩阵，而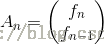

这里是矩阵乘法：1*f(n-1)+1*f(n-2)=f(n); 1*f(n-1)+0*f(n-2)=f(n-1);

这里还是说一下构建矩阵递推的大致套路,一般An与A(n-1)都是按照原始递推式来构建的，当然可以先猜一个An,主要是利用矩阵乘法凑出矩阵T,第一行一般就是递推式，后面的行就是不需要的项就让与其的相乘系数为0。矩阵T就叫做转移矩阵(一定要是常数矩阵),它能把A(n-1)转移到A(n);然后这就是个等比数列，直接写出通项:，此处A1叫初始矩阵。所以用一下矩阵快速幂然后乘上初始矩阵就能得到An,这里An就两个元素(两个位置)，根据自己设置的A(n)对应位置就是对应的值，按照上面矩阵快速幂写法，res[1][1]=f(n)就是我们要求的。

例题：POJ3070

题意：输出斐波那契数列的第n项，n<=1e9；

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<string>
#include<algorithm>
using namespace std;
#define ios1 std::ios::sync_with_stdio(false)
#define ios2 std::cin.tie(0)
#define inf 0x3f3f3f3f
#define ll long long
const int maxn = 5e5+5;
ll mod=10000; //关于取余，依据题意而定
const int edge=2;  //关于矩阵的大小，依据题意而定

struct Matrix //建造矩阵的结构体
{
    ll a[edge][edge];  //构建一个二维的数组，建立一个矩阵
    Matrix()  //关于矩阵的清空
    {
        memset(a,0,sizeof(a));
    }
    Matrix operator *(const Matrix b) //结构体后详细解释
    {
        Matrix temp;
        for(int i=0;i<edge;++i){
            for(int j=0;j<edge;++j){
                for(int k=0;k<edge;++k){
                    temp.a[i][j]+=a[i][k]*b.a[k][j];
                    temp.a[i][j]%=mod;
                }
            }
        }
        return temp;
    }
};
/*****************************

关于operator *:operator为对符号进行重载，在此处即表示对*进行了重新定义
当Matrix结构体里的矩阵遇到了 * 时，就会按照结构体中重新定义的内容进行运算
比如当之后遇到了Matrix类型的a*b时，就会按照所定义的矩阵乘法进行运算，并
返回一个相同类型的temp；

关于本题的此处重载：在函数中实现了矩阵相乘并且对mod取余

***************************/
Matrix m_fpow(Matrix a,ll n) //关于矩阵相乘的快速幂优化
{
    Matrix ans;
    for(ll i=0;i<edge;++i) ans.Mat[i][i]=1; //初始化矩阵为单位矩阵
    while(n!=0){
        if(n&1) ans=ans*a;
        n>>=1;
        a=a*a;
    }
    return ans;
}

int main()
{
    ll n;
    Matrix ans,a,b;
    while(cin>>n&&n!=-1){
        if(n==0) cout<<0<<endl;
        else if(n==1) cout<<1<<endl;
        else {
            a.a[0][0]=a.a[0][1]=a.a[1][0]=1; //初始化最开始的T矩阵
            b.a[0][0]=b.a[1][0]=1; //关于递推式的矩阵，此处代表f(1),f(2);
            ans=m_fpow(a,n-2)*b; //关于本题矩阵快速幂的公式
            cout<<ans.a[0][0]<<endl;//最终的ans.a[0][0]即为f(n);
        }
    }
    return 0;
}

上一串代码，使用了 operator对运算符进行重载，我也是第一次遇到这个玩意，也算是涨知识了吧，不过就在我开心学会新东西的时候，学长跟我讲曾经用这个玩意超时了，然后我又构造函数把这个东西重新敲了一遍，在重敲的过程中发现，对于这类问题最难的不是代码实现，是递推式的找出以及矩阵的构建

#include<iostream>
#include<cstring>
using namespace std;
#define ll long long
const int edge=2;
ll mod = 10000;

//定义一个关于矩阵的结构体
struct Matrix
{
    ll Mat[edge][edge];
    Matrix() { memset(Mat,0,sizeof(Mat)); }
};

//构造函数实现矩阵乘矩阵的运算
Matrix Mat_mul(Matrix a,Matrix b)
{
    Matrix temp;
    for(int i=0;i<edge;++i){
        for(int j=0;j<edge;++j){
            for(int k=0;k<edge;++k){
                temp.Mat[i][j]+=a.Mat[i][k]*b.Mat[k][j];
                temp.Mat[i][j]%=mod;
            }
        }
    }
    return temp;
}

//关于矩阵乘法的快速幂优化
Matrix m_fpow(Matrix a,ll n)
{
    Matrix ans;
    for(ll i=0;i<edge;++i) ans.Mat[i][i]=1;
    while(n!=0){
        if(n&1) ans=Mat_mul(ans,a);
        n>>=1;
        a=Mat_mul(a,a);
    }
    return ans;
}

int main()
{
    ll n;
    Matrix a,b,ans;
    while(cin>>n&&n!=-1){
        if(n==0) cout<<0<<endl;
        else if(n==1) cout<<1<<endl;
        else{
            //关于初始矩阵的初始化
            a.Mat[0][0]=a.Mat[0][1]=a.Mat[1][0]=1;
            b.Mat[0][0]=b.Mat[1][0]=1;
            ans=Mat_mul(m_fpow(a,n-2),b);
            cout<<ans.Mat[0][0]<<endl;
        }
    }
    return 0;
}