从leetcode75 sortColors与快排PARTITION过程说起

最新推荐文章于 2025-06-13 21:19:39 发布

LemintC

最新推荐文章于 2025-06-13 21:19:39 发布

阅读量234

点赞数

分类专栏：杂文章标签： leetcode 快排

本文链接：https://blog.csdn.net/LemintC/article/details/94549317

版权

杂专栏收录该内容

5 篇文章

订阅专栏

从leetcode75 sortColors与快排的PARTITION过程说起

注意
一些前提说明
- 一些前提
问题描述
问题整体分析
解决方法的整体思路
PARTITION过程分析
leetcode75题分析
关于指针变换与元素交换过程的总结分析
扩展1
扩展2
leetcode官方解题思路分析

注意

初始化的时候，各个指针不能相同，如果相同的话，交换过程就会出错，可能会将一个元素进行了多次交换。所以在算法导论的快排中，都是划定A[l,i] 与A[i+1, j-1]。而不是划分为A[l,i-1], A[i,j-1]。如果是后者的话，会将i，j都初始化为l，这样可能会出错的；而前者则是将i初始化为了l-1,j初始化为l，这样就不会出错。所以初始化的时候需要避免所有指针被初始化为了先相同值。通用的做法可以是，给数组增加一个头部，使得每个等价类开始都有一个元素，这样再来初始化指针，就可以保证指针的值是不同的。最后输出数组的时候，需要遍历一遍数组再将这些元素剔除就可以了。所以后面的分析过程以及伪代码都需要修改初始化过程。当然这种做法比较麻烦，任何其他的办法，包括重新规划指针的含义等，只要使得指针初始化的时候值不同就可以了。算法导论的快排中就是通过将i指针的含义进行一点修改就可以了。反正一切的一切都是要确保指针初始化的时候，值一定不能相同

能否利用终止后的指针值，来剔除预先增加的元素呢？从而不需要再遍历一遍数组呢？

一些前提说明

本文试图从leetcode75题与快排的PARTITION的分析中，总结出一些共性的东西。同时针对两种问题分析过程中不同的地方，而这些不同的地方其实也是问题解决过程中的难点与易错点，针对这一点本文尝试使用循环不变式来分析，使得这些易错点与难点的分析更加清晰。

总的说来：从两个问题出发，总结出共性与不同点。对于共性有一套标准的理解方式，对于不同点（即难点易错点），给出一种基于循环不变式的分析思路。

随后使用上述总结的内容来分析两个扩展问题，其一是leetcode75题的扩展，其二则是使用该思路来分析插入排序。

最后就是针对leetcode75题的官方解题思路进行一个分析。以供参考。

一些前提

1、本文中涉及到的输入数据使用数组A[l,r]表示，其中l指向数组的首元素，r指向数组的尾元素。
2、本文所说的指针，在此环境下即默认为数组的下标
3、对于A[l,r]来说，当l<r的时候，即表示数组A为空。此时默认数组A满足所有性质
4、需要读者熟悉快排算法，循环不变式等概念。本文的快排算法参考的是算法导论第三版，具体不在此文进行描述

问题描述

leetcode75题 sortColors：
给定一个数组A[l,r]，其中元素均是0,1,2。将其按照升序排序，要求：原址排序，仅进行一遍数组的遍历扫描操作。

quickSort的PARTITION过程
给定一个数组A[l, r], 将数组A[l, r-1]按照key=A[r]划分成两部分，其中左部分数组的元素<=key, 右部分数组的元素>key。

注：PARTITION过程中操作的实际数组是A[l,r-1]，A[r]仅仅是做为一个key值被使用；而sortColors中被操作的数组是A[l, r]。但这不影响整体问题的说明。

问题整体分析

对于sortColors问题，很直接的想法是使用计数排序，两次遍历完成。但此问题要求仅扫描数组一遍，所以换个思路思考：其不仅仅可以看做是一个排序问题，也可以看做是一个数组的划分问题。将整个数组划分成三类，从左到右依次是等于0的等价类，等于1的等价类，等于2的等价类。

对于PARTITION过程，其就显然是一个数组的划分问题，将数组划分成两类，左边小于等于key的等价类，右边大于key的等价类。

总的来说，这两个问题都是数组的划分问题，当算法运行结束后，数组应该处于一个按照等价类划分好的状态，且对于等价类的之间的次序有固定要求的。

解决方法的整体思路

两个问题解决方法的整体思路是一致的。都是通过多个指针将数组划分成左边的已处理块，右边的待处理块。其中已处理块中，已经将划分好等价类，且等价类之间的次序符合固定的要求了。然后通过一个循环迭代的过程，不断的扩充已处理块，直至待处理块大小为0，即整个数组都成为了已处理块，即整个数组都按照等价类划分好，且等价类之间保持了固定的次序要求。

显然算法的关键就是如何在迭代循环的过程中，扩充左边的已处理块的同时，保持更大的已处理块的性质不变。在这两个问题的解决方案中，都是通过指针的变换操作与元素的交换操作实现的。

指针的变换操作来扩充数组
在指针的变换操作下，通过元素的交换操作，来保证新的更大的已处理数组的性质不变。

以上的整体分析与解决方法的整体思路都是这两个问题的共性，或者说这类问题的共性。而接下来就先说一说，这两个问题中的容易出错的点，即非共性点：

初始指针值的设置。两题都需要通过指针来划分数组，如何划分，怎么设置指针初始值是不同的，也是容易出错的点。
循环迭代的过程中，如何进行指针的变换操作与元素的交换操作？
如何确保循环正好在整个数组成为了已处理块的时候结束？

推荐使用循环不变式来分析上述三点，本文接下来也会使用循环不变式进行分析，并在此基础上给出伪代码。读者会发现，基于循环不变式的分析方法，会使得上述三点中1,2两点的分析过程非常清楚，而这种清楚的好处就是使得代码书写过程更不容易出错。

PARTITION过程分析

注：该过程是对A[l,r-1]进行划分，而A[r]仅仅是做为一个key值使用。

图1
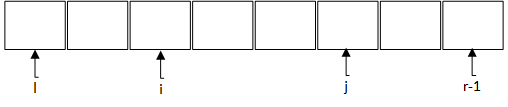
使用4个指针将数组划分成三块
图2
数组的初始划分状态
图3
遍历到的数组元素小于等于key时的指针变换与元素交换操作
图4
遍历到的数组元素大于key时的指针变换与元素交换操作
图5
终止时，数组的指针状态

如图1所示，该过程需要将数组划分成三块，从左到右分别是：小于等于key的块、大于key的块，未处理块。故需要两个指针i，j结合指针l, r-1共四个指针将数组划分成三块。

注：在整个过程中，指针j除了用于划分数组外，同时还指示了下一待处理元素。

循环不变式： A[l,i-1]是小于等于key的元素组成的等价类，A[i, j-1]是大于key的元素组成的等价类，A[j,r-1]是待处理的元素。
初始： 如图2所示，初始时i=l， j=l。那么A[l,i-1]=A[l,l-1]，该子数组为空；A[i,j-1]=A[l,l-1]，该子数组为空；A[j,r-1]=A[l,r-1]，整个数组都处于未处理状态。前文以说，空数组满足所有性质，所以A[l, i-1]，A[i,j-1]符合循环不变式的。
保持： 当遍历到元素A[j]的时候：
1、A[j] <= key，如图3所示。先进行swap(A[i], A[j])，然后i++，再j++。当发现A[j]应该属于小于等于key的等价类的时候，需要扩充A[l,i-1]，然后将该元素A[j]放置到该子数组的尾部。由于该子数组扩充操作抢占了大于key这等价类的空间，所以将A[j]原先位置空出来的空间用于补偿大于key的等价类。这样该等价类的大小没有变化，仅仅是元素的位置做了一些调整。
2、A[j] > key时，如图4所示。直接将j++。这一操作，不仅扩充了大于key的等价类，而且将该元素顺利放置到大于key的子数组的尾部。同时保持小于等于key的子数组不变。
终止： 如图5所示。终止的时候，即待处理数组为空的时候，即A[j,r-1]为空，此时j=r。所以整体数组A[l,r-1]已经划分成了两个等价类，左边的小于等于key的类，以及右边的大于key的类。

PARTITION(A[l,r])
	key = A[r];
	i = l;
	j = l;
	for j = l -> to r-1 //隐含j++
		if A[j] <= key
			swap(A[i], A[j]);
			i++;
			//j++;
		//else
			//j++;

总结：结合循环不变式的分析，理解了指针是如何划分数组，以及如何在迭代过程中进行指针变换，元素交换的同时。一方面扩充已处理数组，一方面保持性质不变。代码就很好写出了。

leetcode75题分析

图6
各指针对数组的划分状态
图7
数组的初始状态
图8
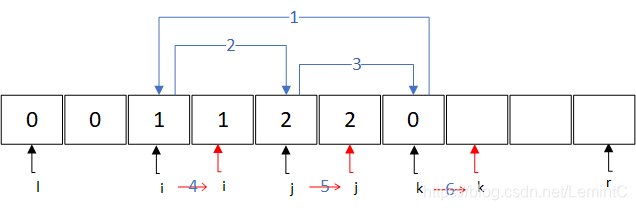
当前访问元素是0的时候的指针变换与元素交换状况
图9
当前访问元素是1的情况时的，指针变换与元素交换过程图10
当前访问元素是2的时候的指针变换与元素交换情况
图11
循环终止时的数组及之后怎状态

如图6所示，该过程中需要将数组划分成四块，从左到右分别是等于0的等价类，等于1的等价类，等于2的等价类，未处理元素。所以需要i，j，k结合l，r共5个指针将数组A[l,r]划分成四块。
注：其中k指针不仅仅用于划分数组，还同时做为遍历数组的指针使用，用于指示下一待处理元素。

循环不变式： A[l,i-1]是等于0的元素的等价类；A[i, j-1]是等于1的元素的等价类；A[j,k-1]是等于2的元素的等价类； A[k,r]未处理元素
初始： 如图7所示，初始时，i=l, j=l, k=l。故A[l,i-1], A[i,j-1], A[j,k-1]都是空数组，而A[k,r]=A[l,r]表示整个数组都是未处理数组。
保持： 当遍历到元素A[k]的时候：
1、若A[k]=0，如图8所示。需要将元素A[k]放置到等价类A[l,i-1]的尾部，即A[i]位置；但是放置到该位置后，抢占了原先属于等价类A[i,j-1]的元素位置，那么就将该被抢占元素，放置到该等价类的尾部，即A[j]位置；这样又抢占了等价类A[j,k-1]的元素位置，那么就将该元素放置到该等价类的尾部，即A[k]位置，而A[k]位置则是当前被处理元素位置，其已经放置到合适的位置了，所以可以直接被抢占。元素通过交换放置好后，分别将i++，j++, k++。更新指针范围，保持循环不变式成立。
2、若A[k]=1，如图9所示。需要将元素A[k]放置到等价类A[i,j-1]的尾部，即A[j]位置；但是放置到该位置后，就抢占了原先属于等价类A[j,k-1]的首元素位置，那么就将该元素放置到该等价类的尾部，即A[k]位置。
相较于上一情况，此时由于等价类A[l,i-1]没有受到影响，所以仅仅需要将j++，k++来更新指针范围就可以了。
3、若A[k]=2，如图10所示。需要将元素A[k]放置到等价类的A[j,k-1]的尾部，即A[k]位置，所以不需要变换。
此时由于，A[l,i-1]，A[i,j-1]都没有受到影响，所以仅仅将k++来更新指针范围就可以了。
综上，三种情况下，进行的指针变换与元素交换等可以保证循环不变式仍然成立。
终止： 终止时，如图11所示。k=r+1，所以A[k,r]为空，即待处理数组为空，所有数组已经处理完成，且保证循环不变式成立。即已经获得了按照0,1,2顺序排序的数组。

伪代码

sortColors(A[l,r])
	i = l;
	j = l;
	k = l;
	for k = l to r //隐含k++
		if A[k] == 0
			tempi = A[i];
			tempj = A[j];
			A[i] = A[k];
			A[j] = tempi;
			A[k] = tempj;
			i++;
			j++;
			//k++;
		else if A[k] == 1
			temp = A[j];
			A[j] = A[k];
			A[k] = temp;
			j++;
			//k++;
		//else
			//k++;

总结：重点就是理解指针如何对数组进行划分的，如何进行的指针变换以及元素交换使得循环不变式在左边数组的扩充情况下仍然保持成立。

关于指针变换与元素交换过程的总结分析

当当前访问元素，属于某个等价类的时候，就需要扩充该等价类的空间，然后将元素放置到该空间。由于各个等价类在数组的左边是连续紧密存放的，所以一个等价类进行了扩充，肯定抢占了其相邻的右侧等价类的位置，所以需要进行调整————将该相邻等价类也向右扩充一个位置，然后将被抢占的元素放置到该位置；同样这次调整又抢占了下一等价类的位置，进行同样操作。以此类推，直至到最后一个等价类，该等价类可以直接扩充到待处理元素，因为该元素已经放置到其所属等价类的尾部了。所以可以直接抢占其位置。

根据这一过程，对划分等价类的各个指针进行变换（即待处理元素及其右侧的等价类的指针统统+1，而左侧的指针统统不变），以及对元素进行交换（即将该等价类的被抢占元素放置到该等价类的末尾，这种放置又抢占了下一等价类的位置，以此类推，直到最后一个等价类，其抢占的是待处理元素的位置，而该元素已经放置到合适的位置了）。

扩展1

sortColors的扩展：输入数组为A[l,r]，其内元素都是0,1,2,3。将数组内的元素按照升序进行排序，要求：原址排序，仅有一次遍历数组的操作。

伪代码：

sortColorsExt(A[l,r])
	i = l;
	j = l;
	k = l;
	p = l;
	for p = l to r //隐含p++
		if A[p] == 0
			tempi = A[i];
			tempj = A[j];
			tempk = A[k];
			A[i] = A[p];
			A[j] = tempi;
			A[k] = tempj;
			A[p] = tempk;
			i++;
			j++;
			k++;
			//p++;
		if A[p] == 1
			tempj = A[j];
			tempk = A[k];
			A[j] = A[p];
			A[k] = tempj;
			A[p] = tempk;
			j++;
			k++;
			//p++;
		if A[p] == 2
			tempk = A[k];
			A[k] = A[p];
			A[p] = tempk;
			k++;
			//p++;
		//else
			//p++;

扩展2

使用这种数组划分的视角来分析插入排序。同样使用数组划分的视角来看待插入排序，通过一个指针i，以及l，r指针将数组分成两部分。左边的已经排好序的子数组，和右边待处理的子数组。

但是与前面不同的是，其在循环过程中不是通过上述那种指针变换与元素交换来保证循环不变式的成立的。而是一个更加麻烦一点的主元素比较，交换的过程来保证左边数组在扩张的过程中，仍然保持循环不变式不变。

数组划分成A[l,i-1]的已经排好序的部分，和A[i,r]的待处理部分。指针i除了用于划分数组外，还指示当前待处理元素。

循环不变式： A[l,i-1]是已经排好序的数组，A[i,r]是待处理数组。
初始： 初始时i=l， A[l,i-1]=A[l,l-1]是空数组，空数组符合所有性质。
保持： 在访问到一个元素后，通过一些比较，交换操作，保证性质仍然成立，且左边数组得到了扩充（详细过程，见后续伪代码，此处关注指针的划分情况）
终止： 终止时，i=r+1，所以A[i,r]这一未处理数组为空，表示整个数组已经完成排序了。

伪代码：

insertionSort(A[l,r])
	i = l;
	for i = l to r //隐含i++
		j = i-1;
		key = A[i];
		while(A[j] > key && j >= l)
			A[j+1]=A[j];
			j--;
		A[j+1] = key;

leetcode官方解题思路分析

其数组划分的方式不同，所以后续指针的变换与元素的交换不同。但仍然是数组划分，指针变换，元素交换这些基本步骤与概念。

其数组是划分成了左侧的等于0部分，右侧的等于2部分，以及中间的待处理部分。

另外其指针的初始化是没有相同值的。