蓝桥杯备赛——3695聪明的小羊肖恩！ 蒟蒻解说

1.首先先看题目：

题目的大概意思：

给出一列数字，并给定最小和最大两个边界值。

问：从这一列数字中成对成对的挑出的两个数，并使这两个数的和在上面提到的最小最大的边界值之间。求出这样的两对数的个数。

2.蒟蒻一开始的想法

作为一个无敌大蒟蒻，一开始上来就想用枚举法，用i和j两个指针，从左往右进行枚举遍历，如果a[i]+a[j] > 最小值 并且 a[i]+a[j] < 最大值，那么就让ans++，最后输出ans

显然如果这样就对了那这题太没有难度了，超时gg。

3.大佬的想法。

首先，先讲数字都录入数组，并且用sort函数进行排序（从小到大）

这里补充一下sort函数的用法：

假设现在有个数组a：

int a[10];

要想对这个数组进行排序，就这么写：

sort(a,a+10);

 第一个是要排序的首地址，第二个是排序的尾地址，是左闭右开的区间

接下来是一个想法的转变：一开始我的想法是求“L <= a[i]+a[j] <= R”这样的条件，实际上可以转变成求 “a[i]+a[j]<=R”和"a[i]+a[j]<=L"的差值

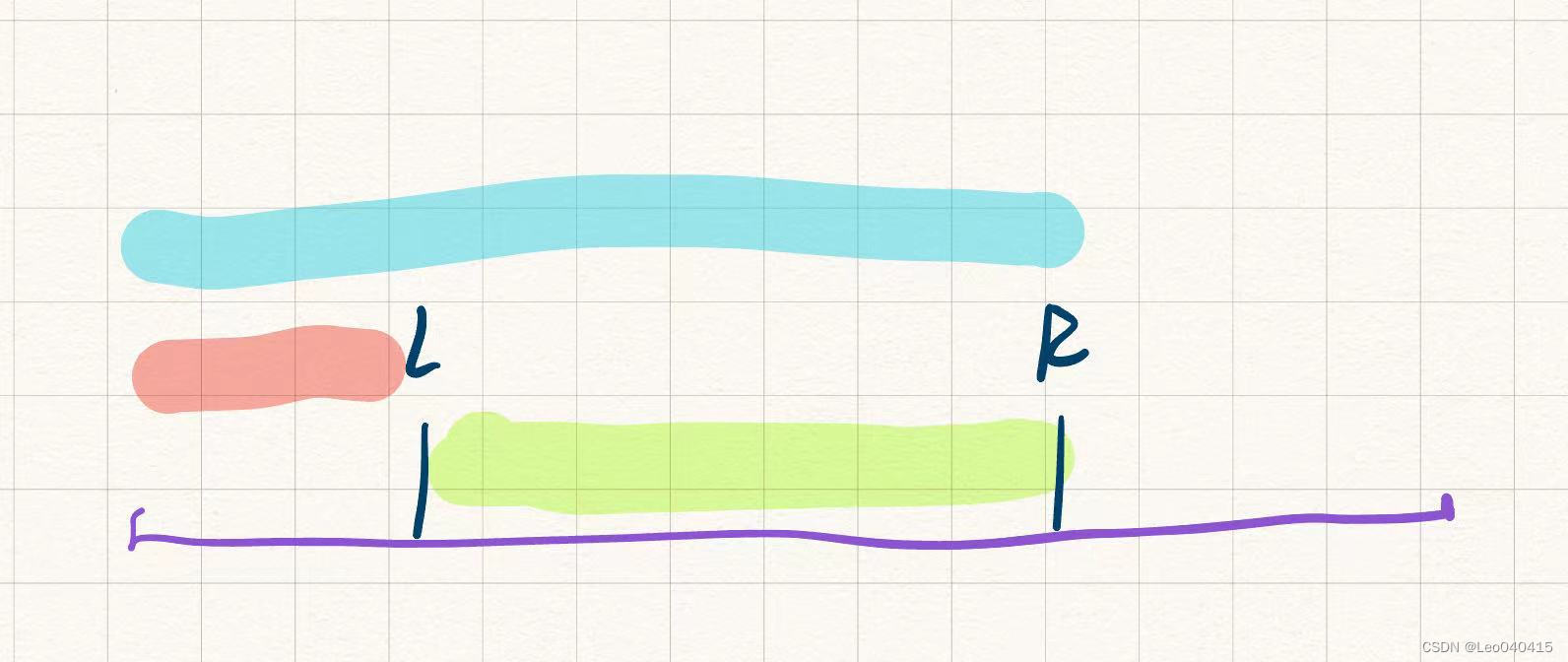
类似于，本来要求绿色的区间，现在可以用R-L区间，也就是蓝色减去红色区间来表示绿色区间。

大佬是怎么寻找数字对的呢？

我们先明确一个事情：当数字是从小到大排序时，左右两头确定好了，左指针不动，右指针往左的都是可以取的。

可以看一下这张图：

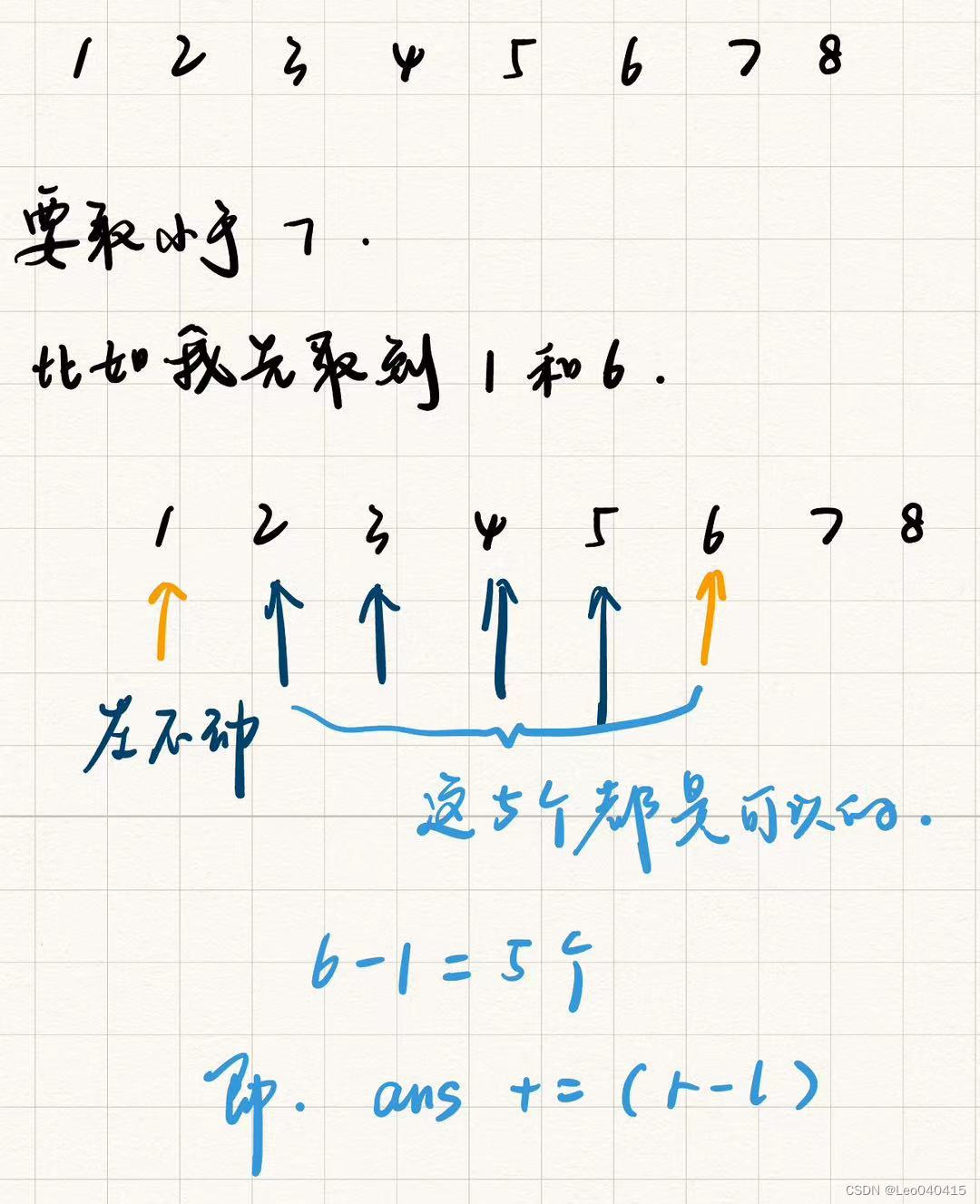
如果发现两个数的和小于等于那个差值，那么左指针向右（因为左指针向右指，数字会变大），并且让ans+=(r-l)；如果大于那个差值，那么让右指针向左（因为左边的数字小）

相信我解释到这里了大家都能看懂了叭~

上大佬代码！！

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6;
int a[N],n;
long long work(int x) {
 long long l = 1,r = n,cnt = 0;
  while(l < r) {
    if(a[l] + a[r] <= x) {
      cnt += r - l;
      l ++;
    }
    else {
      r --;
    }
  }
  return cnt;
}
int main() {
  int l,r;
  cin>>n>>l>>r;
  for(int i = 1; i <= n; i++) cin>>a[i];
  sort(a+1,a+1+n);
  cout<<work(r) - work(l-1);
}

 祝大家新年快乐！