难得一道BZOJ里的非权限莫比乌斯反演题。
筛法求质数时可以将f[]和mu[]求出。
但此题有T组数据,就有点头疼了。
令g(x) = Σ[d|T]f(d)μ(T/d).
对g(x)有贡献的d值很少,具体可以看这篇博客:戳
这篇博客写的很详细,我就不细讲了(原谅我的懒惰qwq)
由于时间限制,对于每组询问分块求,因为对于不同的T,a/T + b/T 的取值只可能有2√a种取法,所以可以分块解决。
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define ll long long
#define N 10000000+100
using namespace std;
int T,tot,a,b,j;ll ans;
int num[N],g[N],prime[N],vis[N];
ll mul[N];
int main()
{
for(int i=2;i<=N;i++){
if(!vis[i]) prime[++tot]=mul[i]=i,g[i]=num[i]=1;
for(int j=1;j<=tot && i*prime[j]<=N;j++){
vis[i*prime[j]]=1;
if(i % prime[j]==0){
num[i*prime[j]]=num[i]+1;
mul[i*prime[j]]=mul[i]*prime[j];
int k=i / mul[i];
if(k==1) g[i*prime[j]]=1;else g[i*prime[j]]=(num[k]==num[i*prime[j]])?-g[k]:0;
break;
}
num[i*prime[j]]=1;
mul[i*prime[j]]=prime[j];
g[i*prime[j]]=(num[i]==1)?-g[i]:0;
}
}
for(int i=1;i<=N;i++) g[i]+=g[i-1];
scanf("%d",&T);
while(T--){
scanf("%d%d",&a,&b);
if(a>b) swap(a,b);
ans=0;
for(int i=1,j;i<=a;i=j+1){
j=min(a/(a/i),b/(b/i));
ans+=(ll)(a/i)*(b/i)*(g[j]-g[i-1]);
}
printf("%lld\n",ans);
}
return 0;
}










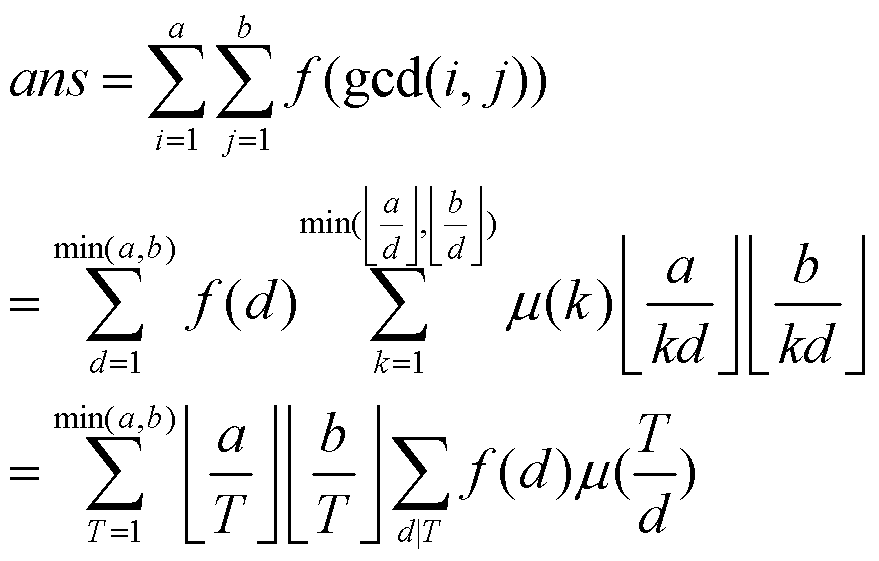














 1466
1466

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








