1、基本的二维几何变换和矩阵表示
1.1平移变换
将平移距离translation distance)tx和ty加到原始坐标(x,y)上获得一个新的坐标位置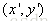
方程1
一对平移距离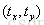
矩阵表示
方程2
使用矩阵形式来表示二维平移方程:
方程3
图1
1.2二维旋转变换
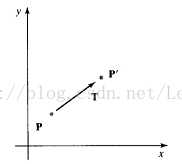
一个对象的二位旋转通过在xy平面上沿圆路径将对象重新定位来实现。二维旋转的参数有旋转角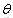
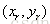
图2
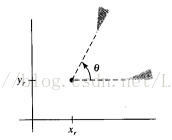
为了简化该基本方法的叙述,我们首先确定当基准点为坐标原点时进行旋转的变换方程。原始点和变换后的点的位置的角度关系如下图所示:
图3
应用标准的三角等式,我们利用角度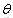
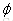
方程4
在极坐标中,点的原始位置为:
方程5
结合上述表达式,我们得到相对于原点,将位置(x,y)的点旋转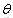
方程6
使用列向量表达式表示坐标位置,那么旋转方程的矩阵形式为:
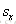
其中旋转矩阵为:
方程8
下面给出绕任意基准点旋转的例子,利用图中的三角关系,可以将方程6规范化为绕任意指定的基准点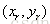
方程9
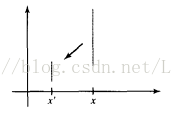
二维缩放变换
一个简单的二维缩放操作可通过将缩放系数(scaling factor)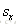
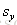
方程10
缩放系数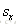
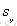
方程11
或者
方程12
当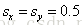
图4








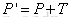
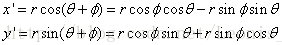
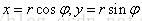
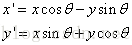
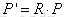
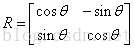
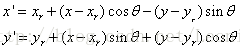
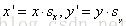
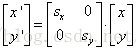
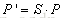














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








