KMP算法

1、 理论部分

1）求序列中前后最长相同子串的长度

1. ** 字符串的前缀：** 字符串的前缀是指 不包含最后一个字符 的 所有以第一个字符（索引为0）开头的连续子串

例如 abcab

前缀子串"a",“ab”，“abc”,“abca”

2. 字符串的后缀：字符串的后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串

例如 abcab

前缀子串"b",“ab”，“cab”,“bcab”

3. 相同前后缀：一个字符串的 所有前缀连续子串 和 所有后缀连续子串 中相等的子串

对于上述例子，相同前后缀为"ab",刚好最长相同前后缀也是他，其长度为 2.

2) 求 next 数组

next 数组的值就是最长前后相同子串的长度，根据上边的最长前后相同子串课求出下边的 next 数组。

索引	0	1	2	3	4
字符串	a	b	c	a	b
next 数组	0	0	0	1	2

3)为什么要求前后最长相同子串

子串有对称属性，如果有对称属性，那么就需要向前查找是否有可以再次匹配的内容。

① 如何理解对称？

例如字符串"abcdabcd"，我们所说的对称也就是“平移”对称。

② 怎么理解向前查找是否有可以再次匹配的内容？

再来看另一个主字符串：“a b c d a b c d a b c d t a b c d”，我们假设一个子串，“a b c d a b c d f”，将他们放在一起

a b c d a b c d a b c d f a b c d

a b c d a b c d f

很显然在 f 处不匹配，但是根据之前求出来的前后最长相同子串，可以看出，当匹配到 f 处才不相同时没说明 f 之前的子串是和主串匹配上了的，那么加下来如何移动子串？

③ 如果把下边的子串指针直接移动到子串首部可行吗？

a b c d a b c d a b c d f a b c d

a b c d a b c d f

仔细看来是不可以的，因为主串中明显含有子串。

④ 那么应该定位到子串哪里？

在这里我们将做如下标记：

(str1: a - d)a b c d (str2: a - d) a b c d a b c d f a b c d

(str3: a - d)a b c d (str4: a - d) a b c d f

根据标红的子串可知，abcd abcd 中 abcd 是平移对称的，那么就可以得到一个关系：str4 = str3，str2 = str1，而前边我们提到主串 a 之前的子串是和子串 f 之前的子串完全匹配上的，那么就可以得到另一个关系str4 = str3 = str2 = str1，也即 str3 = str2。那么也就说明了，主串中的 str2 部分和子串中的 str3 部分是已经匹配上了的，所以接下来只需要从子串的第二个 a 处开始匹配。即：

a b c d a b c d a b c d f a b c d

    a b c d a b c d f

这个时候也就匹配上了，这也是在匹配的时候，当不相同的时候，子串的指针要指向 next[j - 1] 的原因。

2、求 next 数组代码

```java void getNext(int[] next, String s) { int j = 0; next[0] = 0; for (int i = 1; i < s.length(); i++) { while (j > 0 && s.charAt(j) != s.charAt(i)) j = next[j - 1]; if (s.charAt(j) == s.charAt(i)) j++; next[i] = j; } } ```

1）初始化

这里的i指向的是子串的1，而j指向的是0，其实际意义是，j代表前缀子串，而i代表后缀子串(个人理解)

2）逐个查找字符串

这里来看字符串"a g c t a g c a g c t a g c t"

索引 i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
子串	a	g	c	t	a	g	c	a	g	c	t	a	g	c	t
next[i]	0	0	0	0	1	2	3	1	2	3	4	5	6	7	4

这个很简单，我们只要循环遍历这个子串，分别看前1个字符，前2个字符，3个… i个 最后到14 个。

第1个a无对称，所以对称程度0

前两个ag 无对称，所以也是0

依次类推前面0-4都一样是0

前5个agcta，可以看到这个串有一个a相等，所以对称程度为1

前6个agctag，看得到ag和ag对成，对称程度为2

这里要注意了，想是这样想，编程怎么实现呢？

只要按照下面的规则：

a、当前面字符的前一个字符的对称程度为0的时候，只要将当前字符与子串第一个字符进行比较。这个很好理解啊，前面都是0，说明都不对称了，如果多加了一个字符，要对称的话最多是当前的和第一个对称。比如agcta这个里面t的是0，那么后面的a的对称程度只需要看它是不是等于第一个字符a了。

b、按照这个推理，我们就可以总结一个规律，不仅前面是0呀，如果前面一个字符的next值是1，那么我们就把当前字符与子串第二个字符进行比较，因为前面的是1，说明前面的字符已经和第一个相等了，如果这个又与第二个相等了，说明对称程度就是2了。有两个字符对称了。比如上面agctag，倒数第二个a的next是1，说明它和第一个a对称了，接着我们就把最后一个g与第二个g比较，又相等，自然对称成都就累加了，就是2了。

c、按照上面的推理，如果一直相等，就一直累加，可以一直推啊，推到这里应该一点难度都没有吧，如果你觉得有难度说明我写的太失败了。

当然不可能会那么顺利让我们一直对称下去，如果遇到下一个不相等了，那么说明不能继承前面的对称性了，这种情况只能说明没有那么多对称了，但是不能说明一点对称性都没有，所以遇到这种情况就要重新来考虑，这个也是难点所在。

---

上边是一直相同的情况 一，接下来看不同的情况二：

(a g c t a g c )( a g c t a g c) t

我们可以看到这段，最后这个t之前的对称程度分别是：1，2，3，4，5，6，7,倒数第二个c往前看有7个字符对称，所以对称为7。但是到最后这个t就没有继承前面的对称程度next值，所以这个t的对称性就要重新来求。

1、t 如果要存在对称性，那么对称程度肯定比前面这个c 的对称程度小，所以要找个更小的对称，这个不用解释了吧，如果大那么t就继承前面的对称性了。

2、要找更小的对称，必然在对称内部还存在子对称，而且这个t必须紧接着在子对称之后。

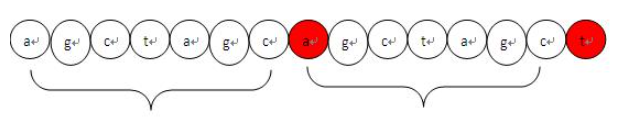
j = 7 此时指向的是红色的 a，而 i 指向的是红色的 t，此刻他们不相等，但是他们之前相同长度的子串是完全匹配上的。那么此时其实对应的就是前边提到的**为什么要求前后最长相同子串？**

理解一：此时也可以将 i 代表的后缀子串和 j 代表的前缀子串拿出来看

a g c t a g c t

a g c t a g c a

用 str 将他们分开：

str1（a g c） t str2 （a g c） t

str3（a g c） t str4 （a g c） a

此时， str4 = str3 = str2 = str1，也即 str3 = str2。那么也就说明了，主串中的 str2 部分和子串中的 str3 部分是已经匹配上了的，所以接下来只需要从子串的 t 处开始匹配。也就是 j = next[j - 1] = next[6] = 3。 即：

a g c t a g c t

​ a g c t a g c t

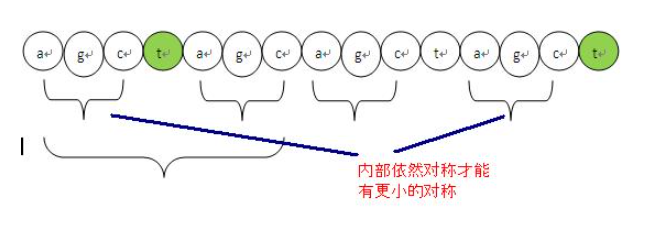
理解二：那么从整体来看，当不同的时候，就需要找更小的对称性，因为对称就可以找到潜藏的已经匹配的字符串信息。下边的四个子串“agc”是完全相同的，我们就可以得知第一个“agc”和最后一个“agc”是相同的，也就是已经匹配上了的。所以下一次 j = 3，也就是从绿色 的 t 处开始匹配，如果匹配上了，就说明他们相等，i 和 j 继续往后走，符合第一种情况；不相等就是第二种情况，继续找，直到 S[j] == S[i] 或 j==0.