一、插入排序

首先,我们将数组中的数据分为两个区间,已排序区间和未排序区间。初始已排序区间只有一个元素,就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
代码:
// 插入排序,a表示数组,n表示数组大小
public void insertionSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 1; i < n; ++i) {
int value = a[i];
int j = i - 1;
// 查找插入的位置
for (; j >= 0; --j) {
if (a[j] > value) {
a[j+1] = a[j]; // 数据移动
} else {
break;
}
}
a[j+1] = value; // 插入数据
}
}
结论:
空间复杂度:O(1) 属于原地排序算法
是否稳定:稳定
时间复杂度:
如果要排序的数据已经是有序的,我们并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置,每次只需要比较一个数据就能确定插入的位置。所以这种情况下,最好是时间复杂度为 O(n)。注意,这里是从尾到头遍历已经有序的数据。
如果数组是倒序的,每次插入都相当于在数组的第一个位置插入新的数据,所以需要移动大量的数据,所以最坏情况时间复杂度为 O(n^2)。
还记得我们在数组中插入一个数据的平均时间复杂度是多少吗?没错,是 O(n)。所以,对于插入排序来说,每次插入操作都相当于在数组中插入一个数据,循环执行 n 次插入操作,所以平均时间复杂度为 O(n^2)。
二、选择排序
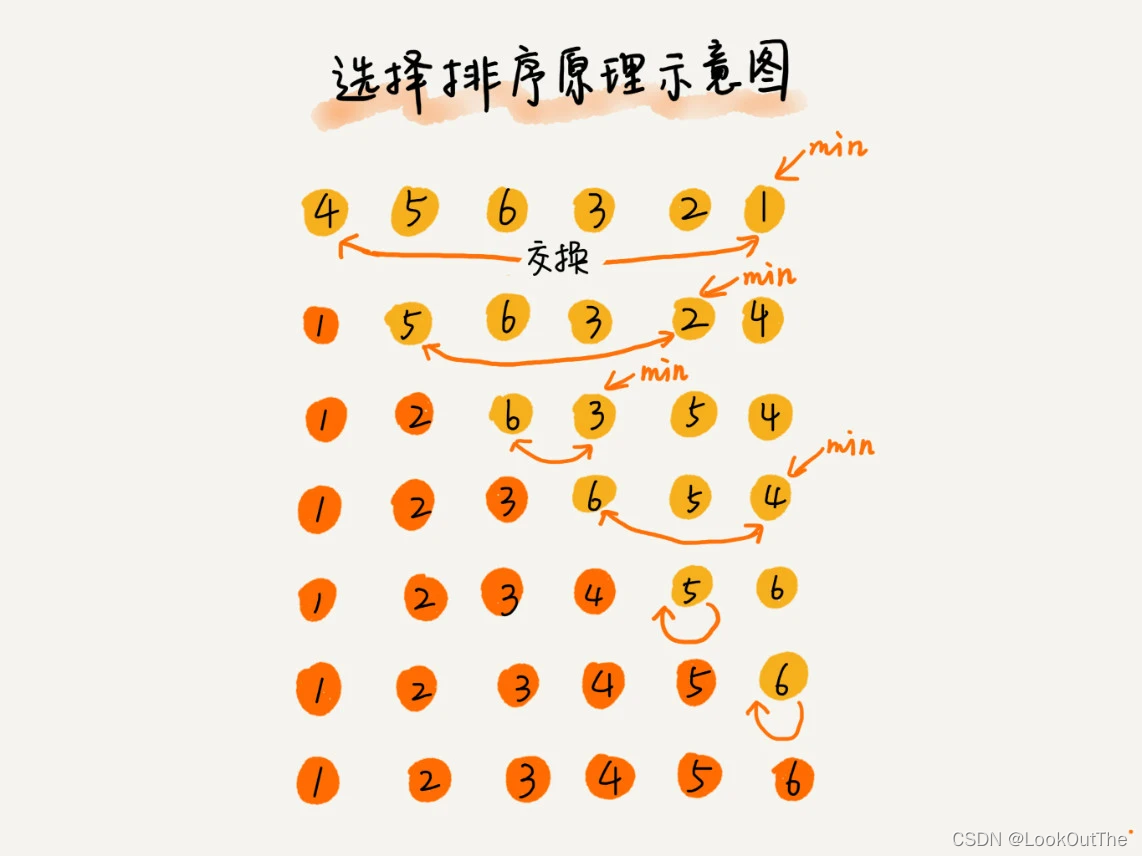
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
代码:
public void selectSort(int[] a, int n){
if(n <=1 ){
return;
}
for (int i = 0; i < n; ++i){
int min = i;
for (int j = i+1; j< n;++j){
if(a[j] < a[min]){
min = j;
}
}
int tmp = a[i];
a[i] = a[min];
a[min] = tmp;
}
}
结论:
空间复杂度:O(1) 原地排序算法
是否稳定:否
时间复杂度:最好、最坏、平均都是O(n^2)
三、总结
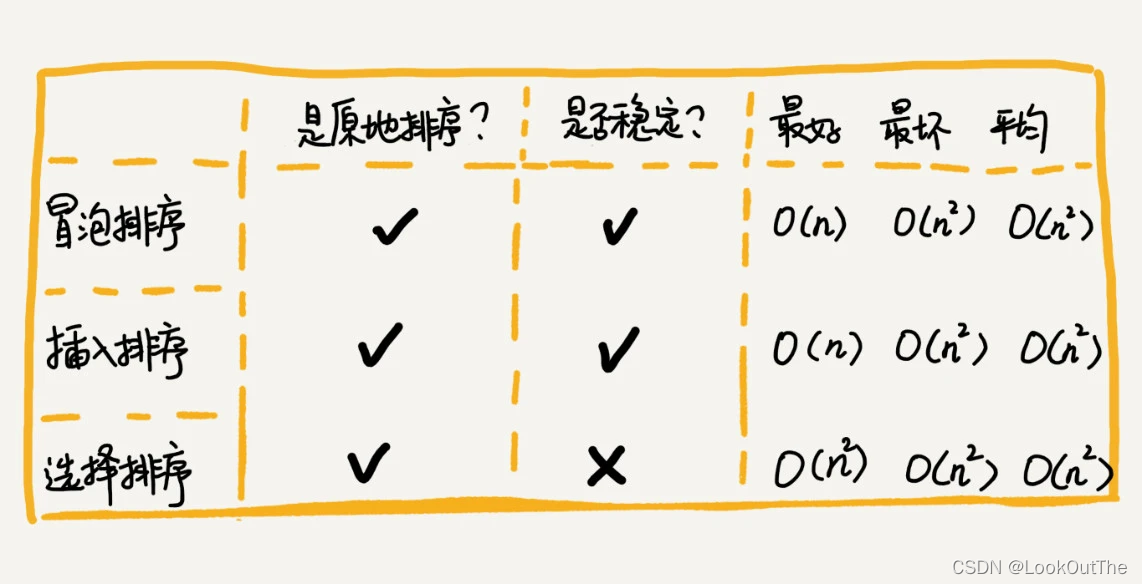





 本文详细介绍了两种基础排序算法——插入排序和选择排序。插入排序在最好情况下时间复杂度为O(n),最坏情况下为O(n^2);而选择排序无论何种情况,时间复杂度均为O(n^2)。这两种算法都是原地排序,空间复杂度为O(1),但选择排序不保证稳定性。
本文详细介绍了两种基础排序算法——插入排序和选择排序。插入排序在最好情况下时间复杂度为O(n),最坏情况下为O(n^2);而选择排序无论何种情况,时间复杂度均为O(n^2)。这两种算法都是原地排序,空间复杂度为O(1),但选择排序不保证稳定性。

















 2659
2659

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










