c++/c语言之用树状数组来进行（区间修改和询问）

LovelyCat_mm

于 2024-06-01 09:45:47 发布

阅读量958

点赞数 29

文章标签： c++ c语言算法数据结构开发语言

本文链接：https://blog.csdn.net/LovelyCat_mm/article/details/139365084

版权

在本篇当中，我们将会讲树状数组。其实这个名字看起来还挺高级的，但相信经过我的介绍，大家可以都听得明白，嗯呐，接下来，我们先详细而系统性地介绍一下树状数组的定义，概念，以及最为重要的编码和应用。

1.树状数组的定义和概念

树状数组或二叉索引树（英语：Binary Indexed Tree），也叫 Fenwick 树，最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题。

树状数组的实质是一种数据结构，可以用来高效地维护一个数列的前缀和，以及支持单点修改、区间查询等操作。它的实现比较简单，能够在 O(log n) 的时间内完成前缀和的查询和单点修改操作，对于支持区间修改和区间查询的问题，可以通过差分的方式来实现。

树状数组的核心思想是将原数列分解成若干个可以直接求和的子区间，从而降低时间复杂度。具体来说，树状数组将原数列的前缀划分为若干个不重叠的区间，每个区间包含的元素数量为 2^k 个，其中 k 是区间所在的层数。树状数组的底层数据结构是一个数组 C，其中 C_i 表示第 i 个元素及其前面的 lowbit(i) 个元素的和。

单点修改时，只需要将被修改元素及其后面的若干个区间的和都进行相应的修改。区间查询时，可以将要查询的区间拆分成若干个覆盖的子区间，每个子区间的求和可以通过一些已经计算好的值来快速计算出来。

可能，家人们有留意到lowbit（i），或许初学者现在还不理解，但没关系，下文会给出这个神奇的lowbit函数的作用以及编写。

我们再用图来演示一下。

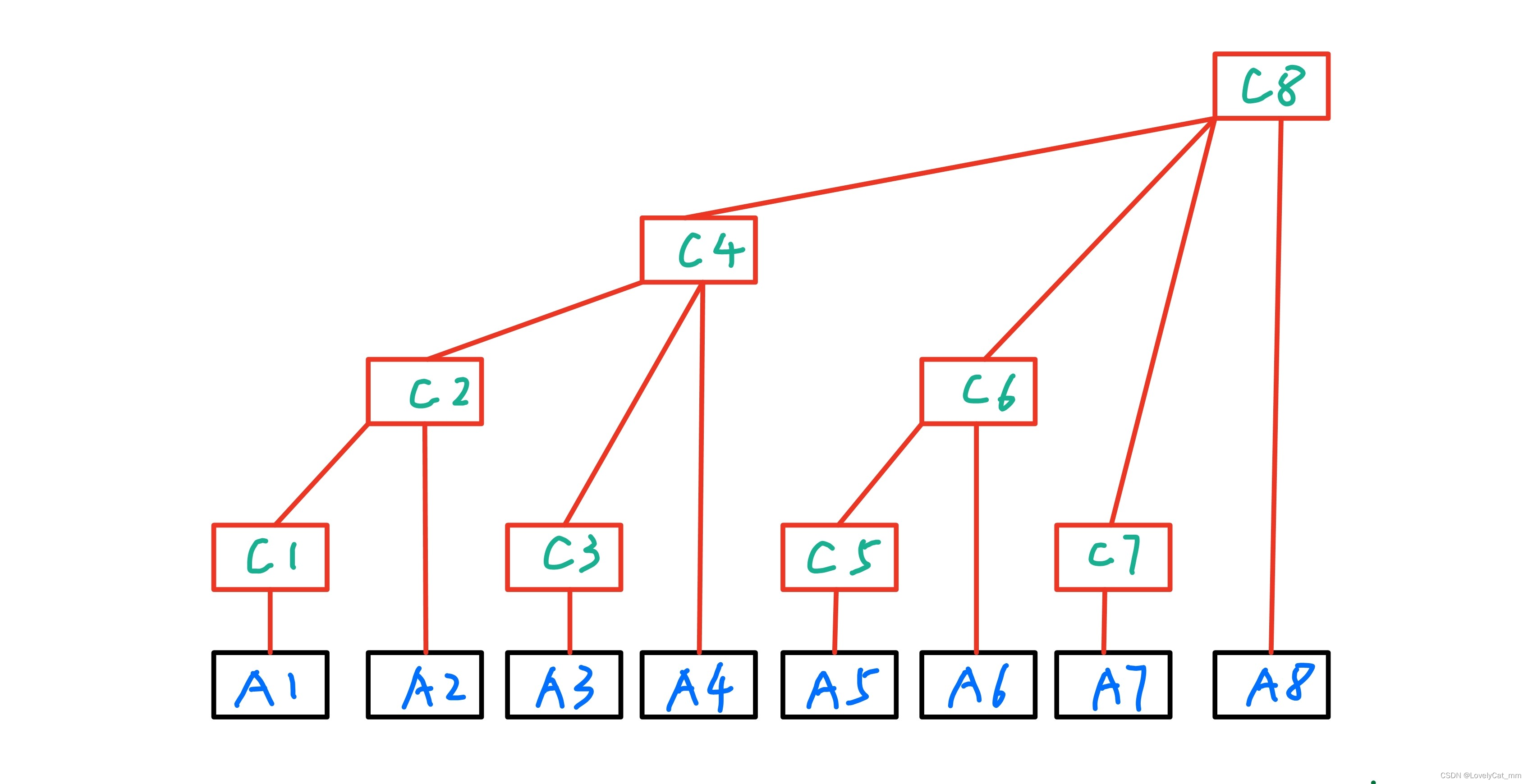
（图片来源：树状数组 - 夜烛灯花 - 博客园 (cnblogs.com)）

对哒，图片来源一个实力不错的大佬。

我们来仔细观察一下图片。这棵树的叶子有A1~A8。而其中C1~C8存储的则是称为树状数组的tree[ ]。一个节点上的tree[ ]的值就是他的树下的直连的字节的和。我们以上图为例，tree[1]=C1=A1，tree[2]=C2=C1+A2，tree[3]=C3=A3，tree[4]=C4=C2+C3+A4，tree[5]=C5=A5，tree[6]=C5+A6，tree[7]=A7，tree[8]=C4+C6+C7+A8。

很奇妙吧，嘻嘻嘻。树状数组一般有两个操作：

（1）查询，也就是求前缀和sum。可能有家人又会问，这怎么又和前缀和有关。是的，所以我才在前一篇铺垫了一下，关于前缀和大家可以翻回前一篇。

既然是求前缀和sum了，那么很容易理解，那就是sum(8)=tree[8]，sum(7)=tree[7]+tree[6]+tree[4]，sum(6)=tree[6]+tree[4]。不行不行，太多了，就打到这吧。

可能，又有家人会问，这个前缀和怎么和前一篇讲的前缀和有出入啊！打咩，先不要惊讶，接下来就是重中之重，查询的规律：

其实很好理解，那就是根据二进制的特性来操作。

比如求sum(7)=tree[7]+tree[6]+tree[4]的具体步骤如下：

First of all，（7）10=（111）2，即7的二进制是111。然后去掉最后的一个1，得到110，也就是6，即tree[6]。

Besides，6的二进制是110。然后去掉最后的一个1，得到100，也就是4，即tree[4]。

Last but not least，4的二进制是100。然后去掉最后的一个1，得到000，就会惊奇的发现，没有了，那就直接return。为什么不加上tree[0]呢，因为tree[0]不用。

最后得出结论：sum(7)=tree[7]+tree[6]+tree[4]。

（2）维护。当元素A1~A8中的某个元素发生改变时，能够以O（log2 n）的时间复杂度来高效地修改tree[ ]的值。

比方说，A4更新了，那么只需要修改tree[4]和tree[8]即可。也就是说，修改它的父节点，以及他的父节点的父节点，以及它的父节点的父节点的父节点......

那么查询有规律，维护呢？

其实，维护的过程是每次在二进制的最后一个1上加上一个1。比如：修改了A4。那么它的详细修改步骤如下：

First of all，4的二进制是100，在最后一个1上加上一个1，得到（1000）2，也就是8，则修改tree[8]。

Besides，8的二进制是1000，在最后一个1上加上一个1，得到（10000）2，也就是16，则修改tree[16]。

Last but not least，继续修改tree[32]，tree[64]。可能有家人会问，那就这么一直修改下去吗？实则不然，定义一个全局而且超大的常量即可，一直加到超过这个常量为止。

最后的最后，那么怎么找到一个是的二进制的最后一个1呢？那么就要用到神奇的lowbit函数了。对哒，就是那个在一开始所说的lowbit函数。

2.神奇的lowbit(x)

lowbit(x)=x&-x，它就是用来找到x的最后一个1的东西。它的原理就是利用了负数的补码表示，补码是原码取反加1。For example，x=6=00000110，-x=11111010，那么lowbit(x)=x&-x=2。

神奇吧，这个lowbit(x)不仅编写简单还很使用。接下来，正式进入正题。

3.树状数组的编码

基于上述原理，下面直接给出树状数组“单点修改+区间查询”的代码。

#include<iostream>
using namespace std;
#define lowbit(x) ((x)&-(x))
#define N 10010
int tree[N];
void update(int x,int d){
	while(x<N){
		tree[x]+=d;
		x+=lowbit(x);
	}
}
int sum(int x){
	int ans=0;
	while(x>0){
		ans+=tree[x];
		x-=lowbit(x);
	}
	return ans;
}
int main(){
	
}

很简单吧，update函数是用来读取数据的，而sum函数则是用来求前缀和的。

其实我们可以很容易看出不管是修改还是查询，它的时间复杂度都为O（nlog2 n），所以总的时间复杂度还是O（nlog2 n）。

接下来，我们再拓展一下。做一个高精度的数组数组。

其实，在竞赛的时候完全没有必要，但我们可以将所学知识串联起来，这样，我们才可以取得进步。

高精度的原理也就是位和借位的处理。高精度加法和高精度减法的原理基本相同，只是在减法中需要处理借位的情况。

以下是高精度加法和高精度减法的简单示例：

高精度加法：将两个大整数从低位到高位逐位相加，如果有进位则需要将进位处理好。例如，计算123456789和987654321的和：

1 2 3 4 5 6 7 8 9 + 9 8 7 6 5 4 3 2 1 —————————— 1 1 1 1 1 1 1 1 1 0

因此，123456789 + 987654321 = 1111111110。

高精度减法：将两个大整数从低位到高位逐位相减，如果有借位则需要将借位处理好。例如，计算987654321和123456789的差：

9 8 7 6 5 4 3 2 1
- 1 2 3 4 5 6 7 8 9
——————————
8 7 7 4 9 8 5 3 2

因此，987654321 - 123456789 = 864197532。

下面直接给出高精度加法和高精度减法的代码。

#include <iostream>
#include <string>
#include <algorithm>
std::string add(const std::string &a, const std::string &b) {
    std::string result;
    int carry = 0;
    int temp;
    for (size_t i = 0; i < a.length() || i < b.length(); ++i) {
        temp = carry;
        if (i < a.length()) temp += a[a.length() - 1 - i] - '0';
        if (i < b.length()) temp += b[b.length() - 1 - i] - '0';
        carry = temp / 10;
        result += (temp % 10) + '0';
    }
    if (carry > 0) result += carry + '0';
    std::reverse(result.begin(), result.end());
    return result;
}
int main() {
    std::string num1, num2;
    std::cin >> num1 >> num2;
    std::string sum = add(num1, num2);
    std::cout << sum << std::endl;
    return 0;
}

这是高精度加法。

#include <iostream>
#include <string>
#include <algorithm>
std::string sub(std::string &a, std::string &b) {
	std::string result;
	int tw = 0;
	int temp=0;
	bool flag = false;
	if(a.size()<b.size()){
		flag=true;
		swap(a,b);
	}
	if(a.size()==b.size()){
		if(a<b){
			flag=true;
			swap(a,b);
		}
	}
	for (size_t i = 0; i < a.length() || i < b.length(); ++i) {
		temp -= tw;
		if (i < a.length()) temp += a[a.length() - 1 - i] - '0';
		if (i < b.length()) temp -= b[b.length() - 1 - i] - '0';
		if (temp < 0) {
			temp = 10 + temp;
			tw = 1;
		} else {
			tw = 0;
		}
		result += temp + '0';
		temp=0;
	}
	if (tw > 0) result += tw + '0';
	if (flag)result += '-';
	std::reverse(result.begin(), result.end());
	return result;
}
int main() {
	std::string num1, num2;
	std::cin >> num1 >> num2;
	std::string ans = sub(num1, num2);
	std::cout << ans << std::endl;

	return 0;
}

这是高精度减法代码。

其实有了模板以后，高精度树状数组也就很简单了，直接就可以套用模板，将三样东西串起来即可。下面我用类写了一个高精度的树状数组。

具体代码如下：

#include<iostream>
#include<map>
#include<string>
#include<algorithm>
using namespace std;
#define lowbit(x) ((x)&-(x))
#define N 10010
typedef class Binary_Indexed_Tree {
	public:
		void update(int x, string value);
		string sum(int x);
		Binary_Indexed_Tree(int length): size(length) {};
	private:
		typedef struct node {
			string str;
			node operator +(node &a) {
				node b;
				int temp, jw = 0;
				for (size_t i = 0; i < this->str.size() || i < a.str.size(); i++) {
					temp = jw;
					if (i < this->str.size())temp += this->str[this->str.size() - 1 - i] - '0';
					if (i < a.str.size())temp += a.str[a.str.size() - 1 - i] - '0';
					jw = temp / 10;
					b.str += (temp % 10) + '0';
				}
				if (jw > 0)b.str += jw + '0';
				std::reverse(b.str.begin(), b.str.end());
				return b;
			}
			node operator -(node &a) {
				node b;
				int tw = 0;
				int temp = 0;
				std::string s1 = this->str, s2 = a.str;
				bool flag = false;
				if (this->str.size() < a.str.size()) {
					flag = true;
					swap(this->str, a.str);
				}
				if (this->str.size() == a.str.size()) {
					if (this->str < a.str) {
						flag = true;
						swap(this->str, a.str);
					}
				}
				for (size_t i = 0; i < this->str.length() || i < a.str.length(); ++i) {
					temp -= tw;
					if (i < this->str.length()) temp += this->str[this->str.length() - 1 - i] - '0';
					if (i < a.str.length()) temp -= a.str[a.str.length() - 1 - i] - '0';
					if (temp < 0) {
						temp = 10 + temp;
						tw = 1;
					} else {
						tw = 0;
					}
					b.str += temp + '0';
					temp = 0;
				}
				if (tw > 0) b.str += tw + '0';
				if (flag) {
					b.str += '-';
					this->str = s1;
					a.str = s2;
				}
				std::reverse(b.str.begin(), b.str.end());
				return b;
			}
		} data;
		int size;
		map<int, string> Tree;
} bit;
void Binary_Indexed_Tree::update(int x, string value) {
	node a, b, c;
	b.str = value;
	if (value[0] != '-')
		while (x < size) {
//			tree[x]+=d;
			a.str = Tree[x];
			c = a + b;
			Tree[x] = c.str;
			x += lowbit(x);
		} else while (x < size) {
//			tree[x]+=d;
			a.str = Tree[x];
			c = a - b;
			Tree[x] = c.str;
			x += lowbit(x);
		}
}
string Binary_Indexed_Tree::sum(int x) {
	node ans, a, b;
	while (x > 0) {
		a.str = Tree[x];
		b.str = ans.str;
		ans = a + b;
		x -= lowbit(x);
	}
	return ans.str;
}
int main() {
    
	return 0;
}

这就是本篇的全部内容了，如果有哪里讲的不好或者不对，请家人们指出。

好心的家人们支持一下本宝宝吧，本宝宝打字不易，恳求各位三连，谢谢。

（侵删）

LovelyCat_mm

关注

29
点赞
踩
22

收藏

觉得还不错? 一键收藏
0
评论
c++/c语言之用树状数组来进行（区间修改和询问）

我们以上图为例，tree[1]=C1=A1，tree[2]=C2=C1+A2，tree[3]=C3=A3，tree[4]=C4=C2+C3+A4，tree[5]=C5=A5，tree[6]=C5+A6，tree[7]=A7，tree[8]=C4+C6+C7+A8。其实这个名字看起来还挺高级的，但相信经过我的介绍，大家可以都听得明白，嗯呐，接下来，我们先详细而系统性地介绍一下树状数组的定义，概念，以及最为重要的编码和应用。然后去掉最后的一个1，得到000，就会惊奇的发现，没有了，那就直接return。
复制链接

扫一扫