B树与B+树详解-CSDN博客

本文链接：https://blog.csdn.net/Luck_Ape/article/details/79475994

 
 一、概念 

 
 索引：索引（index）是帮助mysql高效获取数据的一种数据结构。 

  数据库查询是数据库的主要功能之一，最基本的查询算法是顺序查找（linear search）时间复杂度为O(n)，显然在数据量很大时效率很低。优化的查找算法如二分查找（binary search）、二叉树查找（binary tree search）等，虽然查找效率提高了。但是各自对检索的数据都有要求：二分查找要求被检索数据有序，而二叉树查找只能应用于二叉查找树上，但是数据本身的组织结构不可能完全满足各种数据结构（例如，理论上不可能同时将两列都按顺序进行组织）。所以，在数据之外，数据库系统还维护着满足特定查找算法的数据结构。这些数据结构以某种方式引用（指向）数据，这样就可以在这些数据结构上实现高级查找算法。这种数据结构就是索引。 

 
 二、B-Tree和B+Tree 

 
 目前大部分数据库系统及文件系统都采用B-Tree或其变种B+Tree作为索引结构。 

 
 B-Tree 

 
 为了描述B-Tree，首先定义一条数据记录为一个二元组[key, data]，key为记录的键值，对于不同数据记录，key是互不相同的；data为数据记录除key外的数据。那么B-Tree是满足下列条件的数据结构： 

d>=2，即B-Tree的度；
h为B-Tree的高；
每个非叶子结点由n-1个key和n个指针组成，其中d<=n<=2d；
每个叶子结点至少包含一个key和两个指针，最多包含2d-1个key和2d个指针，叶结点的指针均为NULL；
所有叶结点都在同一层，深度等于树高h；
key和指针相互间隔，结点两端是指针；
一个结点中的key从左至右非递减排列；
如果某个指针在结点node最左边且不为null，则其指向结点的所有key小于v(key1)，其中v(key1)为node的第一个key的值。
如果某个指针在结点node最右边且不为null，则其指向结点的所有key大于v(keym)，其中v(keym)为node的最后一个key的值。
如果某个指针在结点node的左右相邻key分别是keyi和keyi+1且不为null，则其指向结点的所有key小于v(keyi+1)且大于v(keyi)。图2是一个d=2的B-Tree示意图。

 
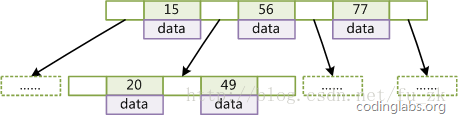
   由于B-Tree的特性，在B-Tree中按key检索数据的算法非常直观：首先从根节点进行二分查找，如果找到则返回对应节点的data，否则对相应区间的指针指向的节点递归进行查找，直到找到节点或找到null指针，前者查找成功，后者查找失败。B-Tree上查找算法的伪代码如下： 
  
   BTree_Search(node, key) {
    if(node == null) return null;
    foreach(node.key)
    {
        if(node.key[i] == key) return node.data[i];
            if(node.key[i] > key) return BTree_Search(point[i]->node);
    }
    return BTree_Search(point[i+1]->node);
}
data = BTree_Search(root, my_key); 关于B-Tree有一系列有趣的性质，例如一个度为d的B-Tree，设其索引N个key，则其树高h的上限为logd((N+1)/2)，检索一个key，其查找结点个数的渐进复杂度为O(logdN)。从这点可以看出，B-Tree是一个非常有效率的索引数据结构。 
  
   B+Tree 
  
   B-Tree有许多变种，其中最常见的是B+Tree，例如MySQL就普遍使用B+Tree实现其索引结构。 
  
   与B-Tree相比，B+Tree有以下不同点： 
  
 每个结点的指针上限为2d而不是2d+1。
 内结点不存储data，只存储key；叶子结点不存储指针。
 
   图3是一个简单的B+Tree示意。

 
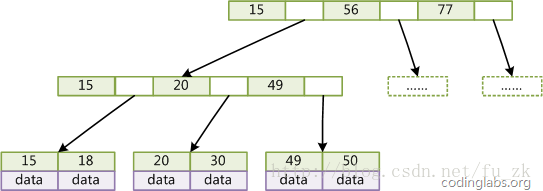
   由于并不是所有节点都具有相同的域，因此B+Tree中叶结点和内结点一般大小不同。这点与B-Tree不同，虽然B-Tree中不同节点存放的key和指针可能数量不一致，但是每个结点的域和上限是一致的，所以在实现中B-Tree往往对每个结点申请同等大小的空间。 
  
   一般来说，B+Tree比B-Tree更适合实现外存储索引结构，具体原因与外存储器原理及计算机存取原理有关，将在下面讨论。 
  
   带有顺序访问指针的B+Tree 
  
   一般在数据库系统或文件系统中使用的B+Tree结构都在经典B+Tree的基础上进行了优化，增加了顺序访问指针。

 
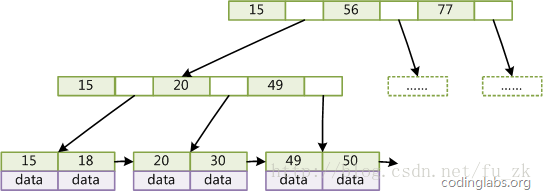
   如图4所示，在B+Tree的每个叶子结点增加一个指向相邻叶子结点的指针，就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能，例如图4中如果要查询key为从18到49的所有数据记录，当找到18后，只需顺着结点和指针顺序遍历就可以一次性访问到所有数据结点，极大提高了区间查询效率。 
  

 
   这一节对B-Tree和B+Tree进行了一个简单的介绍，下一节结合存储器存取原理介绍为什么目前B+Tree是数据库系统实现索引的首选数据结构。 
  

 
   二、最左前缀原理与相关优化 
  

 
   最左前缀：即查询时根据where字段后的值在建立的所有索引中从左开始匹配适合的索引。 
  

    以下四种情况说明最左匹配的情况，以联合索引 
   `uk_loanid_terms` (`loan_id`,`terms`)为例： 
  

 
   1、顺序执行sql。 
  

    执行结果： 
  

     正常情况下执行计划很完美，走了定义的索引。 
   

 
    2、非顺序执行sql。 
   

      以下两种情况执行计划相同，如下： 
    

     MySQL内部会根据条件字段做一个索引合并的优化，虽然查询的字段不是按照联合索引的顺序，但是其内部会调整为所需要的索引结构，然后按照索引去查。因为条件中所需的 
    最左字段(loan_id)存在。 
   

 
    3、少组合索引中的一个字段值，但不是最左值。 
   

     执行计划结果 
   

     这个sql中少了联合索引中的terms字段，仍然走了索引，但是这个时候extra中出现了Using where,这表示在走索引查询到的结果集的基础上又使用了where条件过滤了数据，并非是完全走索引出来的结果。性能肯定较完全走索引差了些。 
   
    4、缺少组合索引中的最左值。

     执行结果 
   

     这个sql少了联合索引中 
    最左字段loan_id,因此索引匹配失败，执行全表扫描，性能最差。 
   

     综上，可以在一些sql书写的过程中，适当的关联一些联合索引中的字段，来使完整的匹配sql，从而提高sql查询性能，即使有些字段是非必须的。 
   

Mysql_索引