最大连续字串和的加强版。
1 -1 2 2 3 -3 4 -4 5 -5Hit:In the sample, we choose {2,2,3,-3,4} and {5}, then we can get the answer.
即求两段不重叠连续字串的最大和
第一反应是枚举每个点作为断点,两段分别求最大连续子串和,取最大值
#include <stdio.h>
#define N 50005
int a[N],dp[N];
int main()
{
int t, n, max1, max2, max3;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%d",&a[i]);
max3 = -1000000000;
dp[1] = max1 = a[1];
for(int k=2; k<=n; k++)
{
dp[k] = max2 =a[k];
for(int i=k+1; i<=n; i++)
{
if(dp[i-1]>0)
dp[i] = dp[i-1] + a[i];
else
dp[i] = a[i];
max2 = max2 < dp[i] ? dp[i] : max2;
}
if(max3<max1 + max2)
max3 = max1 + max2;
if(dp[k-1]<0)
dp[k] = a[k];
else
dp[k] = a[k] + dp[k-1];
if(max1 < dp[k])
max1 = dp[k];
}
printf("%d\n",max3);
}
return 0;
}于是怒TLE了。。。
原因是以每点为断点是该点后的连续子串和都重新求一遍,时间复杂度为O(n2)
聪明的做法是,顺序、逆序各求一次最大连续子串和,这样可避免重复计算,时间复杂度为O(n)
#include <stdio.h>
#define N 50005
int a[N],dp[N],rdp[N];
int left[N],right[N];
int main()
{
int t, n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%d",&a[i]);
//顺序
dp[1] = a[1];
for(int i=1; i<=n; i++)
dp[i] = dp[i-1]>0 ? dp[i-1]+a[i] : a[i];
//test=====================================
//for(int i=1; i<=n; i++)
// printf("%d ",dp[i]);
//printf("\n");
//test=====================================
//逆序
rdp[n] = a[n];
for(int i=n-1; i>=1; i--)
rdp[i] = rdp[i+1]>0 ? rdp[i+1]+a[i] : a[i];
//test=====================================
//for(int i=1; i<=n; i++)
// printf("%d ",rdp[i]);
//printf("\n");
//test=====================================
//左起前i个元素的连续子序列最大和
left[1] = dp[1];
for(int i=2; i<=n; i++)
left[i] = dp[i]>left[i] ? dp[i] : left[i-1];
//test=====================================
//for(int i=1; i<=n; i++)
// printf("%d ",left[i]);
//printf("\n");
//test=====================================
//右起
right[n] = rdp[n];
for(int i=n-1; i>=1; i--)
right[i] = rdp[i]>right[i+1] ? rdp[i] : right[i+1];
//test=====================================
//for(int i=1; i<=n; i++)
// printf("%d ",right[i]);
//printf("\n");
//test=====================================
int ans = -100000000;
for(int i=1; i<n; i++)
ans = left[i]+right[i+1]>ans ? left[i]+right[i+1] : ans;
printf("%d\n",ans);
}
return 0;
}







 本文介绍了一种改进的连续子串和算法,通过顺序和逆序求解避免重复计算,有效提升时间效率。
本文介绍了一种改进的连续子串和算法,通过顺序和逆序求解避免重复计算,有效提升时间效率。
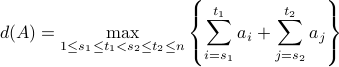
















 793
793

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








