常见的二叉树（Binary tree）结构

二叉树（Binary tree）

二叉树（Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

二叉树的性质

1. 二叉树第i层上的结点数目最多为  个节点（，根节点层数为 1）。
2. 深度为k的二叉树最多有  个节点（，根节点深度为 0）。
3. 若在任意一棵二叉树中，有  个叶子节点，有  个度为2的节点，则必有 

完全二叉树 

假设有一个二叉树的深度为n，除了第n层以为，其它各层的结点数都达到最大个数（1~n-1层的节点都是满的），且第n层（最下面一层）的所有结点都连续集中在最左边。

 满二叉树

除根节点以外，每一层上的所有结点都有两个子结点的即为满二叉树

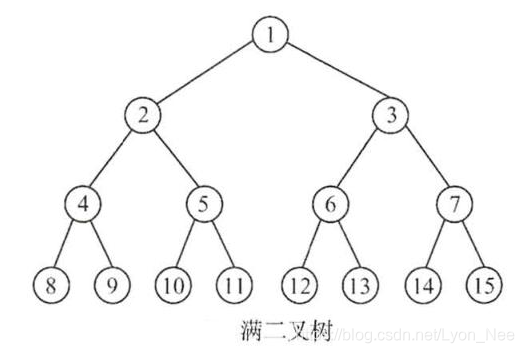
 满二叉树是完全二叉树的特例，因为满二叉树已经满了。

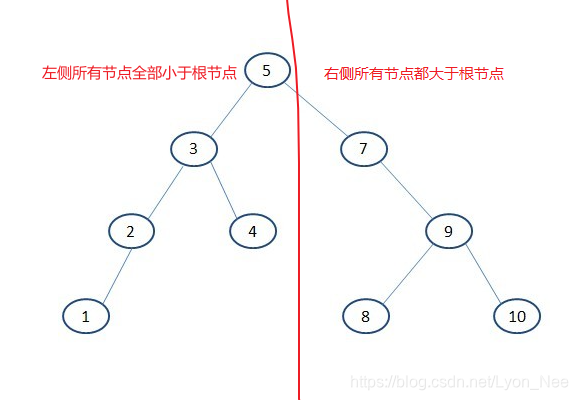
二叉排序树（二叉查找树）

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

它的左、右子树也分别为二叉搜索树。

平衡二叉树

平衡二叉树是特殊的二叉排序树

平衡因子 = 左子树的高度 - 右子树的高度

每个节点平衡因子的绝对值<=1，且满足二叉排序树定义的数即为平衡二叉树

 

到此结束。

有问题，或者建议请留言，谢谢。

Golang二叉树的4种遍历方式（先序，中序，后序，层序）