KMP算法的简单理解 【笔记】

//本文除实现代码外全部为原创内容 转载请注明出处  代码来自这里

kmp算法是一种改进的字符串匹配算法，由D.E.Knuth与V.R.Pratt和J.H.Morris同时发现，故称KMP算法

字符串匹配：从字符串T中寻找字符串P出现的位置（P远小于T）。其中P称为“模式”。

KMP算法对模式串进行O(m)的预处理后只需对文本T扫描一次即可找到匹配，所以时间复杂度为O(n+m)。

先不管O(m)的预处理，直接看O(n)的扫描。

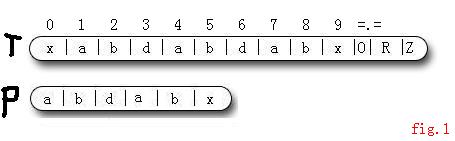
对于下图的字符串匹配：(图1)

1 ：i=0 , j=0 , 判断T[i] != P[j]，则 i++.

2 ： i=1, j = 0 , T[i]==P[j] , 则i++,j++

--------------

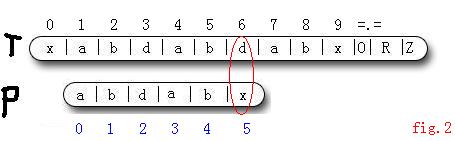
3 ： 依次判断T[2...5] == P [1...4] , 此时i = 6, j = 5 . T[i] != P[j] . （图2）

如果使用BF算法, i 指针在此时匹配失败后会回溯, 然后重新进行匹配 .

KMP算法中则不对 i 指针进行回溯, 而是修改 j 指针. 此时执行操作 j = next[j] = 2 , 继续进行匹配; 其中next[]数组是通过O(m)的预处理求得的, 暂时不管

--------------

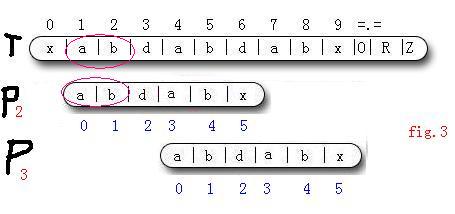
4：（图3中, P2的 j 指针是图2中的 j 指针）由于我们从T[1]开始匹配直到T[6]才出现匹配失败的情况, 所以T[1...5]==P[0...4]. 很明显图中圈出的两个串相等, 即 P[0 , 1] == T[1 , 2]

--------------

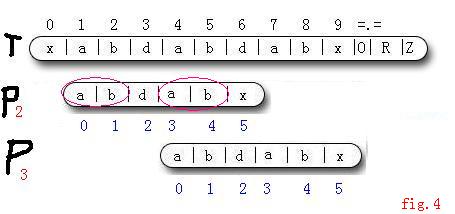
5：通过观察我们又能发现, P[0 , 1] == P[3 , 4]; （这就是O(m)预处理出的next[]数组中值的意义 , next[5] = 2 , 则P[0...2-1] == P[5-2...5-1]）

同步骤4，由于直到T[6]才出现匹配失败, 所以又P[3 , 4] == T[4 , 5] . 所以P[0 , 1] == T[4 , 5].

在对 j 指针进行 j = next[j] 操作后, P3 [0 , 1] 就对应着P2 [3 , 4]. 即P3[0 , 1] == T［4 , 5] . 所以KMP算法才会直接将j 指针跳到2而不是0 , 省去了对前一部分的匹配 , 也保证了不会漏掉匹配

6：P[0...5] == T[4...9] , 匹配成功.

--------------

在对next[]的预处理中 , 如果找不到一个像上面的P[2]一样合适的位置 , 就只能从P[0]开始匹配 , 并且在当前的 i 位置不会找到匹配了 ,所以next = -1. 程序执行j = next[j] = -1后 , 在下一次循环中 判断j==-1 就执行i++,j++. 通过这样处理, 省去了 i 指针的回溯 , 降低了时间复杂度 . 因为这样操作每次匹配无论成功还是失败都会有 i++ , 所以时间复杂度是O(n)

C/C++ code:

int KMPMatch(char *s,char *p)
{
    int next[100];
    int i,j;
    i=0;
    j=0;
    getNext(p,next);	//预处理求next[]
    while(i<strlen(s))
    {
        if(j==-1||s[i]==p[j])
        {
            i++;
            j++;
        }
        else
        {
            j=next[j];       //消除了指针i的回溯
        }
        if(j==strlen(p))	//匹配成功
            return i-strlen(p);
    }
    return -1;
}

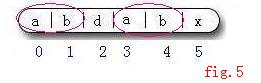
接下来再看O(m)的预处理。回顾一下刚刚的模式字符串P（图5）

我们刚刚用到了j = next[j] = next[5] = 2, 当时j =5 , j-1 =4 .

观察位置2的性质. 在子串P[0...j-1]即 P[01234] 中 , P[0]P[1] == P[3]P[4] 即 P[0...2-1] == P[5-2...5-1]

也就是说, 串P[0]P[1]即串P[3]P[4]既是字串P[0...4]的真前缀, 又是它的真后缀. 重新看图4就能明白 , 只要满足这个性质, 就能保证语句 j = next[j] 的正确性.  

结论 若next[j]=k , 则k为满足 P[0...k-1] == P[j-k ... j-1] 且 k<j 的最大值. 如果找不到这样的k , next[j]=-1.

  显然next[0]=-1 , next[1] = 0

预处理的方法(这里只介绍递推方法)

如果有next[j]=k, 则有P[0...k-1] == P[j-k ... j-1]

1) 如果P[j] == P[k]

 P[0...k-1] + P[k]  == P[j-k ... j-1] + P[j]   即  P[0...k] == P [j-k ... j]

所以next[j+1] = k + 1 = next[j] + 1

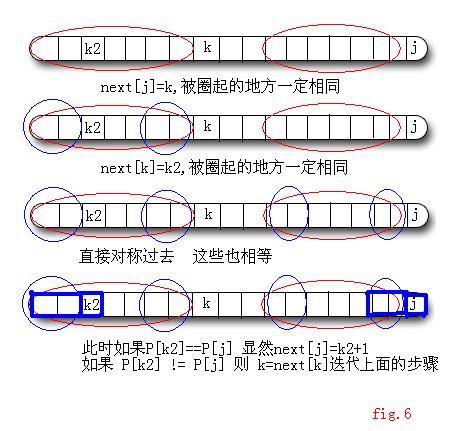
2) 如果P[j] != P[k], 那么可以看做模式匹配的问题,匹配失败的时候, 显然k=next[k].

具体：（图6）设next[j]=k, next[next[j]] = next[k] = k2

C/C++ code:

void getNext(char *p,int *next)
{
    int j,k;
    next[0]=-1;
    j=0;
    k=-1;
    while(j<strlen(p)-1)
    {
        if(k==-1||p[j]==p[k])    //匹配的情况下,p[j]==p[k]
        {
            j++;
            k++;
            next[j]=k;
        }
        else                   //p[j]!=p[k]
            k=next[k];
    }
}