logistic 回归

转载 许愿  https://blog.csdn.net/qq_32095939/article/details/76358955

 

Logistic回归

例：企业到金融商业机构贷款，金融商业机构需要对企业进行评估。评估结果为 0 , 1 两种形式，0 表示企业两年后破产，将拒绝贷款，而 1 表示企业 2 年后具备还款能力，可以贷款。在表 6 中，已知前 20 家企业的三项评价指标值和评估结果，试建立模型对其他 5 家企业（企业 21-25）进行评估。

代码：

clc, clear, close all
X0=xlsread('logistic_ex1.xlsx', 'B2:D21'); % 回归模型的输入
Y0=xlsread('logistic_ex1.xlsx', 'E2:E21'); % 回归模型的输出
X1=xlsread('logistic_ex1.xlsx', 'B2:D26'); % 预测数据输入
GM = fitglm(X0,Y0,'Distribution','binomial');
Y1 = predict(GM,X1);
N0 =1:size(Y0,1); N1= 1:size(Y1,1);
plot(N0', Y0, '-kd');
hold on; scatter(N1', Y1, 'b')
xlabel('数据点编号'); ylabel('输出值');

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

这里fitglm函数，将数据传入后，第三个参数表示离散分布，第四个参数表示二项分布（fitglm有很多用法，具体可help fitglm，这里只用到到了这个来做Logistic回归分析）。此函数返回一个Model（官方文档就叫这个），然后在predict函数中，第一个参数传入的参数类型就是Model，所以将上面函数得到的返回值传入，然后将需要预测的数据输入，既得预测的结果Y1。

注：scatter函数，画气泡图的函数。

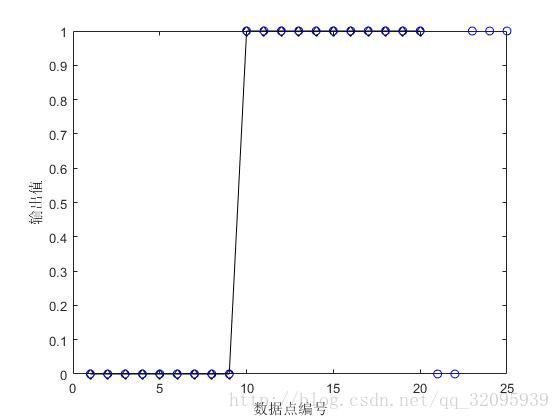
这里Y1也是从1到26每个都有的，图片里20以前的的气泡和原始给的数据绘制重叠在一起了。

这里再将GM这个模型输出。

整体p-value的值很小，模型很显著。

回归方程为：

y(x)~-239.81-2.0957*X1+12.99*X2+233.38*X3

方程得到的值大于0则预测值为1，小于0则预测值为0。

这里验证了一下。

i=1;
while i<=25
    %X1(i,1)
    yy(i)=-239.81-2.0957*X1(i,1)+12.99*X1(i,2)+233.38*X1(i,3);
    i=i+1;
end
yy

• 1
• 2
• 3
• 4
• 5
• 6
• 7

与预测值对比，可得，方程得到的值大于0则预测值为1，小于0则预测值为0。