博弈论

博弈论

看了两天博弈，做了一点题，写一写，把自己学会的东西记录下来。

巴什博奕（Bash Game）

只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜.

威佐夫博奕（Wythoff Game）

有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

尼姆博奕（Nimm Game）

有三堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

一、必败点（P点）和必胜点( N点)

必败点（P点）：前一个选手将取胜的位置，意思是说当某人位于P点时，此人必败。
必胜点（N点）：下一个选手将取胜的位置，意思是说当某人位于N点时，此人必胜。

二、必败(必胜)点属性

① 所有终结点是必败点（P点）；

②从任何必胜点（N点）操作，至少有一种方法可以进入必败点（P点）；

③无论如何操作， 从必败点（P点）都只能进入必胜点（N点）。

三、状态标记的步骤

步骤1:将所有终结位置标记为必败点（P点）；

步骤2: 将所有一步操作能进入必败点（P点）的位置标记为必胜点（N点）

步骤3:如果从某个点开始的所有一步操作都只能进入必胜点（N点） ，则将该点标记为必败点（P点） ；

步骤4: 如果在步骤3未能找到新的必败（P点），则算法终止；否则，返回到步骤2。

四、Graph Games  & Sprague-Grundy Function

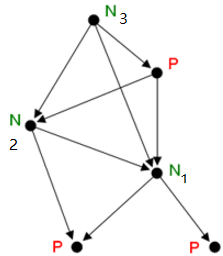
可以用一个有向无环图（From）来表示游戏的状态：

由上面的“二、必胜/败点属性”，我们可以归纳出：

①一个没有出度的点是P状态点；

②一个点是P状态当且仅当该点任何后继都是N状态；

③一个点是N状态当且仅当该点存在后继是P状态。

Sprague-Grundy 函数给游戏中的每个状态分配了一个自然数，节点v的Grundy值等于没有在v的后继的Grundy值中出现的最小自然数。设mem为求得这个最小自然数的函数，同时，称该最小自然数为最小排斥值。

P状态点的Grundy值为0。

令N = {0, 1, 2, 3, ...} 为自然数的集合，S为一个有限子集，且S ⊂ N；

则：mex S = min (N S)。

先将所有P点的Grundy值都标记为0；

N1：因为后继只有0，所以Grundy值为1；

N2：因为后继有0、1（N1），所以Grundy（N2）=mem（Grundy（N1），0）=2；

N3：因为后继有0、2（N2），所以Grundy（N3）=mem（Grundy（N2），0）=3。

记点v的Grundy值为g（v），令图为G（v，e），则Sprague-Grundy函数满足两个重要性质：
①点v是一个P-状态当且仅当g(v)=0
②如果G = G1 + G2 且 v = v1v2 是G的一个状态，那么g(v) 为g(v1) 和 g(v2) 在二进制下的异或：即g(v) = g(v1) ⊕ g(v2)。运算⊕也称作nim和。

自己整理的Nim游戏中求SG值的模板函数：

一堆：

int x,k,a[MAXN];//x是总数，k是a中元素的个数，a是可以取的数目
bool sg[MAXN];//SG值
void solve()
{
    sg[0]=false;
    for(int j=1; j<=x; ++j)
    {
        sg[j]=false;
        for(int i=0; a[i]<=j&&i<k; ++i)
            if(!sg[j-a[i]])
                sg[j]|=!sg[j-a[i]];
    }
    if(sg[x]) puts("Alice");//最后取光的
    else puts("Bob");
}

N堆：

int n;//n堆
int k;//可取情况的数目
int x[MAXN];//n堆分别的数目
int a[MAXN];//可取情况
int sg[MAXN];//等价于Nim中的石子数
void solve()
{
    sg[0]=0;//轮到自己还剩0枚时是必败态
    int Max=*max_element(x,x+n);
    for(int i=1; i<=Max; ++i)
    {
        set<int>s;//存储当前所能到达状态的sg值
        for(int j=0; j<k; ++j)
            if(a[j]<=i)
                s.insert(sg[i-a[j]]);
        int cnt=0;//寻找当前状态的最小排斥值
        while(s.count(cnt)!=0)//返回值为cnt的元素个数
            ++cnt;
        sg[i]=cnt;
    }
    int res=0;
    for(int i=0; i<n; ++i)
        res^=sg[x[i]];
    if(res)puts("Alice");//先手必胜
    else puts("Bob");
}

五、有分割游戏

        如果一个状态分割之后是两个状态,那么SG中就插入这两个后继状态的XOR.

        在Nim中，不论有几堆石子、初始状态是怎样的，只要XOR的结果相同，那么对胜负是没有影响的。这里也一样，只要SG值相同，即使发生分割，只要堆分割后的各部分取XOR，就可以利用这一个SG值来代表几个游戏复合而成的状态，SG值也可以同样地计算。

比如：

HDU 2311-Nim or not Nim?（Nim博弈-打sg表找规律）  
sg[j]^sg[i-j];//是可以分成两堆的情况

POJ 2311-Cutting Game（Nim博弈-sg函数/记忆化搜索） 

当一张w*h的纸被分成两张时，假设所得的两张纸的sg值分别为sg1和sg2，

则它们对应的状态的sg值可以表示为sg1 XOR sg2。

先写这么多，会随着自己的做题和理解继续修改或者补充~