POJ 1149-PIGS（Ford-Fulkerson 标号法求网络最大流）

PIGS

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 20029		Accepted: 9178

Description

Mirko works on a pig farm that consists of M locked pig-houses and Mirko can't unlock any pighouse because he doesn't have the keys. Customers come to the farm one after another. Each of them has keys to some pig-houses and wants to buy a certain number of pigs. 
All data concerning customers planning to visit the farm on that particular day are available to Mirko early in the morning so that he can make a sales-plan in order to maximize the number of pigs sold. 
More precisely, the procedure is as following: the customer arrives, opens all pig-houses to which he has the key, Mirko sells a certain number of pigs from all the unlocked pig-houses to him, and, if Mirko wants, he can redistribute the remaining pigs across the unlocked pig-houses. 
An unlimited number of pigs can be placed in every pig-house. 
Write a program that will find the maximum number of pigs that he can sell on that day.

Input

The first line of input contains two integers M and N, 1 <= M <= 1000, 1 <= N <= 100, number of pighouses and number of customers. Pig houses are numbered from 1 to M and customers are numbered from 1 to N. 
The next line contains M integeres, for each pig-house initial number of pigs. The number of pigs in each pig-house is greater or equal to 0 and less or equal to 1000. 
The next N lines contains records about the customers in the following form ( record about the i-th customer is written in the (i+2)-th line): 
A K1 K2 ... KA B It means that this customer has key to the pig-houses marked with the numbers K1, K2, ..., KA (sorted nondecreasingly ) and that he wants to buy B pigs. Numbers A and B can be equal to 0.

Output

The first and only line of the output should contain the number of sold pigs.

Sample Input

3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6

Sample Output

7

Source

Croatia OI 2002 Final Exam - First day

题目意思：

有M个猪圈，N个顾客，给出每个猪圈中猪的数目。

每个顾客有A把钥匙，对应A个猪圈的编号，每个顾客会买B头猪。

Mark木有猪圈的钥匙，每个顾客来的时候把他们有钥匙的猪圈全部打开；而且Mark可以重新分配被打开的猪圈里面的猪。

顾客离开后，猪圈再次被锁上。

求Mark能卖出的猪的最大值。

解题思路：

Ford-Fulkerson 标号法求网络最大流。

除了顾客的N个顶点外，自己增加源点和汇点这两个点。

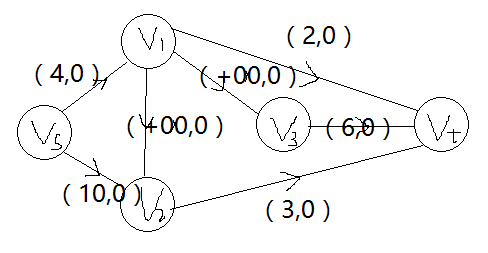
每个顾客购买的数目是连接到汇点上的容量；

源点与每个猪圈的第一个顾客连边，边的容量是开始时猪圈中猪的数目；

若源点与某个结点之间有重边，将权合并（如上图中Vs~V1，4就是合并了1和3）；

若顾客j紧跟i后面打开猪圈，那么<i，j>容量为正无穷（因为此时可以随意调整猪圈中的猪的数量）。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <iomanip>
#include <algorithm>
#define maxn 1010
#define INF 0xfffffff
using namespace std;
struct ArcType
{
    int c,f;//容量、流量
};

ArcType edge[maxn][maxn];
int n,m;//顶点数、弧数
int s,t;
int flag[maxn];//顶点状态：-1——未标号；0——已标号未检查；1——已标号已检查
int prev[maxn];//标号的第一个分量：指明标号从哪个顶点而来，以便找出可改进量
int alpha[maxn];//标号的第二个分量：可改进量α
int que[maxn];//相当于BFS中的队列
int v;//队列头元素
int qs,qe;//队首队尾的位置
int i,j;

void ford()//标号法求网络最大流
{
    int flow[maxn][maxn];//节点之间的流量Fij
    int prev[maxn];//可改进路径上前一个节点的标号，相当于标号的第一个分量
    int minflow[maxn];//每个顶点的可改进量α，相当于标号的第二个分量
    int que[maxn];
    int qs,qe;//队列首尾位置坐标
    int v,p;//当前顶点、保存Cij-Fij
    for(i=0; i<maxn; ++i)
        for(j=0; j<maxn; ++j)
            flow[i][j]=0;
    minflow[0]=INF;//源点标号的第二分量为无穷大
    while(1)//标号法
    {
        for(i=0; i<maxn; ++i)//每次标号前，每个顶点重新回到未标号状态
            prev[i]=-2;
        prev[0]=-1;
        qs=0;
        que[qs]=0;//源点入队
        qe=1;
        while(qs<qe&&prev[t]==-2)
        {
            v=que[qs];//取队列头节点
            ++qs;
            for(i=0; i<t+1; ++i)//prev[i]==-2表示顶点i未标号
                if(prev[i]==-2&&(p=edge[v][i].c-flow[v][i]))//edge[v][i].c-flow[v][i]!=0能保证i是v邻接顶点且能进行标号
                {
                    prev[i]=v;
                    que[qe]=i;
                    ++qe;
                    minflow[i]=(minflow[v]<p)?minflow[v]:p;
                }
        }
        if(prev[t]==-2) break;//汇点t无标号，标号法结束
        for(i=prev[t],j=t; i!=-1; j=i,i=prev[i])//调整过程
        {
            flow[i][j]+=minflow[t];
            flow[j][i]=-flow[i][j];
        }
    }
    for(i=0,p=0; i<t; ++i)//统计进入汇点的流量即最大流的流量
        p+=flow[i][t];
    cout<<p<<endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>m>>n;//顶点个数、弧数
    s=0,t=n+1;//源点和汇点
    int pig[maxn],last[maxn];//每个猪圈中猪的数量、每个猪圈前一个顾客的序号
    memset(last,0,sizeof(last));
    for(i=1; i<=m; ++i)
        cin>>pig[i];//输入每个猪圈中猪的数量
    for(i=1; i<=n; ++i)
    {
        int num;
        cin>>num;//拥有的猪圈钥匙数量
        for(j=0; j<num; ++j)
        {
            int k;
            cin>>k;//钥匙编号
            if(last[k]==0)
                edge[s][i].c+=pig[k];
            else edge[last[k]][i].c=INF;
            last[k]=i;
        }
        cin>>edge[i][t].c;
        edge[i][t].f=0;
    }
    n+=2;//加上源点和汇点
    ford();
    return 0;
}
/*
3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6
*/