Educational Codeforces Round 132 (Rated for Div. 2) D

链接

题意

给你一个n×m的网格，只不过行是从上到下，从左到右的。然后每一列，从下到上有连续的阻碍，现在给你机器人的文起始位置和终点位置，你不能去有阻碍的地方，也不能超出网格，然后给你一个k，你一次性只能上下左右连续走k步，现在又q次询问，问你是否能够到达目的地。

思路

首先题目中说了，我们一次行走过程只能走k步，不能多不能少，那么我们可以一下就想到第一种情况：
1.起点和终点的横纵坐标的差值一定是k的倍数，不然怎么都到不到。
2.然后这个题的标签是数据结构，那么就往数据结构上面靠。现在我们想一下，满足了第一种情况后，该怎么走，如下图：（绿色代表是阻碍，蓝色是起点，粉色时终点，其实只要晓得两个点就行。）

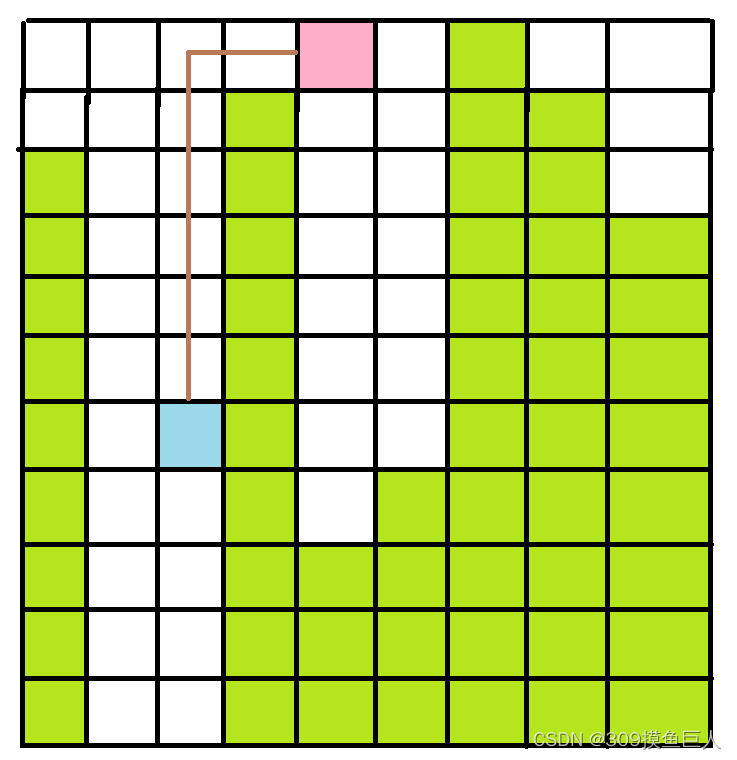
现在两个点要走通，那么只能按照棕色的线走，那么我们反过来想，两个点怎么才是走不通的？假设我们设这两个点之间障碍最大的的纵坐标为x，那么是不是我们必须从这个纵坐标上面走过去即可，所以我们这里要找到这两个点之间阻碍最大的高度即可，所以我们可以用线段树来维护。
代码如下：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 2e5 + 10;

int n, m;
int a[N];
int q;
int x1, y1, x2, y2, k;

struct node
{
    int l, r;
    int maxn;
}tr[N << 2];

void pushup(int u) { tr[u].maxn = max(tr[u << 1].maxn, tr[u << 1 | 1].maxn); }

void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if (l == r) { tr[u].maxn = a[l]; return ; }

    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

int query(int u, int l, int r)
{
    if (l <= tr[u].l && r >= tr[u].r) return tr[u].maxn;

    int mid = tr[u].l + tr[u].r >> 1;
    int maxx = 0;
    if (l <= mid) maxx = query(u << 1, l, r);
    if (r > mid) maxx = max(maxx, query(u << 1 | 1, l, r));
    return maxx;
}

void solve()
{
    cin >> n >> m;
    for (int i =  1; i <= m; i ++) cin >> a[i];

    build(1, 1, m);

    cin >> q;
    while (q --)
    {
        cin >> x1 >> y1 >> x2 >>y2 >> k;

        if (abs(x1 - x2) % k || (y1 - y2) % k) { cout << "NO\n"; continue; }
        int tmp = query(1, min(y1, y2), max(y1, y2));
        x1 += (n - x1) / k * k;

        cout << (x1 > tmp ? "YES" : "NO") << endl;
    }
}

signed main()
{
    std::ios::sync_with_stdio(false);

    solve();

    return 0;
}