图论(1)——图的基本概念

图的概念

图的定义

二元组(V(G),E(G))称为图。
其中， V(G)是非空集合，称为结点集
E(G)是V(G)诸结点之间边的集合
常用G=(V,E)表示图

即结点数|V|=n, 边数|E|=m

边

$e_k=(v_i,v_j)(称v_i和v_j是相邻结点,或者e_k分别与v_i,v_j相关联)$
有向图:
$v_i是e_k的始点，v_j是e_k的终点$
无向图:
$v_i,v_j是e_k的端点$

• 自环(圈) 只有一个结点相关联的边
• 重边、多重图 同一对结点之间存在多条边

度

G=(V,E)的某结点v所关联的边数称为该结点的度，用 d(v)表示。如果v带有自环，则自环对d(v)的贡献为2
有向图中:

出度(正度)$d^{+}(v)$: 以结点v为始点的边的数目
入度(负度)$d^{-}(v)$: 以结点v为终点的边的数目
$d(v)=d^{+}(v)+d^{-}(v)$

例子:

特殊的图

• 简单图: 任意两结点间最多只有一条边，且不存在自环的无向图
• 空图: 没有任何边的简单图(V, Ø), 用$N_n$表示
  若此时恰有|V|=1, 称为平凡图
• 完全图: 任何两个结点间都有边的简单图, 用$K_n$表 示
  $K_n$中每个节点的度都是n-1

图的性质

• Handshaking Theorem
  设G=(V, E)有n个结点，m条边，则 ${\sum }_{v\in V(G)}d(v)=2m$

• G中度为奇数的结点必为偶数个．

• 有向图G中正度之和等于负度之和．

• Kn的边数是n(n-1)/2.

• 非空简单图G中一定存在度相同的结点．
  鸽巢原理
  度d(v)的取值范围是 1~(n-1)

权

每条边赋以一个实数$w_k$作为权
都是正实数：正权图

子图

• 给定G=(V, E), 如果存在另一个G’=(V’, E’), 满足V’$\in$V, E’$\in$ E, 则称G’是G的一个子图
• 特别地，如果V’=V, 就称G’是G的支撑子图或者生成子图(spanning subgraph)
• 如果V’$\in$V, 且E’包含了G在结点子集V’之间的所有边, 则称G’是G的导出子图(induced subgraph)
• G自身既是支撑子图，又是导出子图；
• 空图是G的支撑子图；
• G自身和空图称为平凡子图

图的运算

给定两个图G1=(V1,E1),G2=(V2,E2). 令

• G1$\cup$G2=(V,E),其中V=V1$\cup$V2,E=E1$\cup$E2;

• G1$\cap$G2=(V,E),其中V=V1$\cap$V2,E=E1$\cap$E2;

• G1$\oplus$G2=(V,E),其中V=V1 $\cup$ V2,E=E1$\oplus$E2;
  注意这里节点是并
  分别称为G1和G2的并，交和对称差

• G-H

  • 表示在G中删去一个子图H，即删掉H中的各条边(支撑子图)
  • 特别地，对于简单图G，称Kn-G为G的补图

• G -v 表示从G中删去结点v及其关联的边(导出子图)

• G-e 表示从G中删去边e(生成子图)

• $G+e_{i}j表示在G中增加某条边e_k=(v_i,v_j)$

邻点集

• 无向图的邻点集 Γ(v)={u|(v, u)$\in$E}

• 设v是有向图G的一个结点，则 ${\Gamma }^{+}$(v)={u|(v, u)$\in$E}
  称为v的直接后继集或者外邻集;

• 相应地 ${\Gamma }^{-}$(v)={u|(u, v)$\in$E} 称为v的直接前趋集或者内邻集

图的同构

定义

两个图G1=(V1, E1), G2=(V2, E2),如果V1和V2之间存在双射f, 而且(u, v)$\in$E1, 当且仅当(f(u), f(v))$\in$E2时, 称G1和G2同构
记作G1≅G2

必要条件（用来判断不是）

1. |V(G1)|=|V(G2)|, |E(G1)|=|E(G2)|
2. G1和G2结点度的非增序列相同
3. 存在同构的导出子图(用来判断不同构)

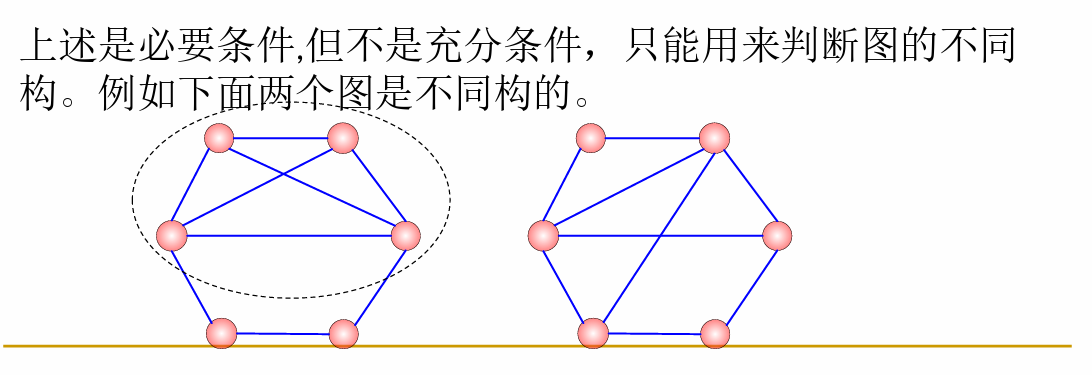
右图中不存在与左图中圈住部分同构的子图

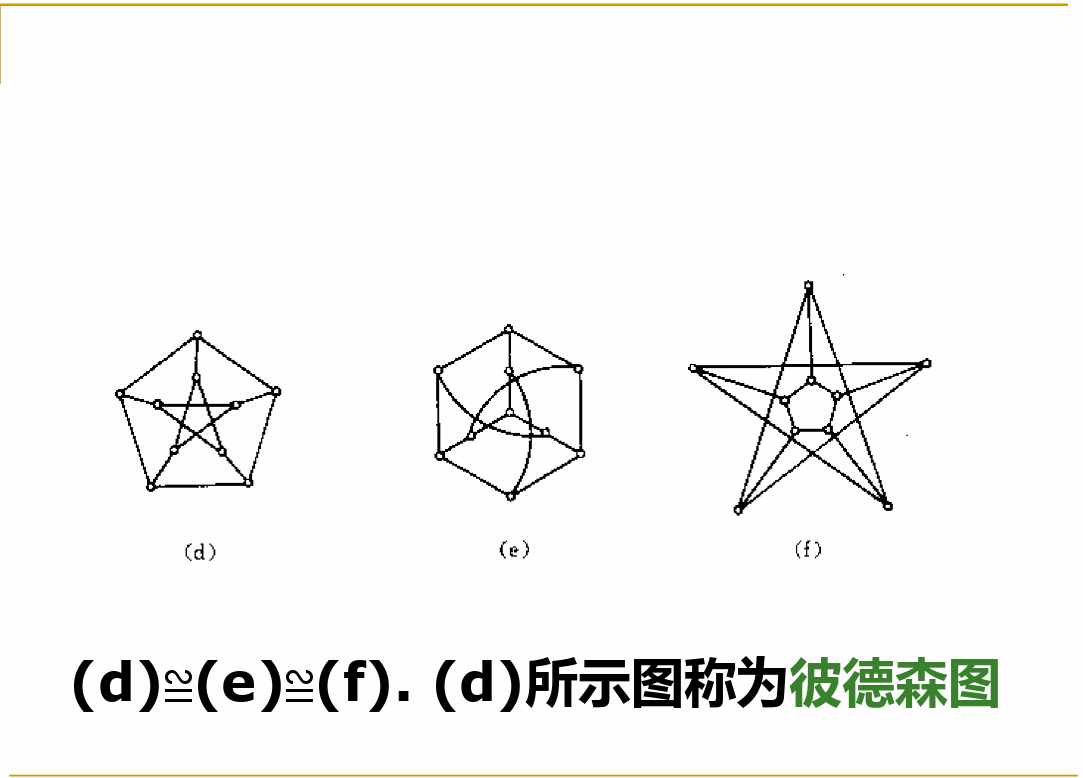
图的代数表示

邻接矩阵(Adjacency Matrix)

• A[i,j]=1 , 如果i至j有 一条无向边；
• 可以表示自环
• 无法表示重边
• 有向图:
  • $v_i$出度: i行之和;
  • $v_j$入度: j列之和
• 无向图:
  • 对称矩阵
  • $v_i$结点的度: i行或i列之和

权矩阵

关联矩阵(Incidence Matrix)

• 有向图:
  • B[i,j]=1, 如果$v_i$是边ej=($v_i,v_k$)的始点
  • B[i,j]=-1, 如果$v_i$是边ej=$(v_k,v_i$)的终点
• 无向图: 没有-1, 1(如果是端点)
• 可以表示重边
• 无法表示自环

邻接表

• 可以表示重边和自环
• 与矩阵相比,更节约空间

图的应用

路线数量

求任意两个节点之间刚好能两步到达的路线数量?
把2个邻接矩阵相乘,得到矩阵的第i行j列的数字就是从节点i到j的路线数量.

状态转移图

状态看作点，状态间的转化看作边
Q: 三个量杯容量分别是8升，5升，3升，现8升的量杯装满了水，问怎样才能把水分成2个4升的。
初始状态(8,0,0)，终止状态(4,4,0)
A: (8,0,0)→(5,0,3)→(5,3,0)→(2,3,3) →(2,5,1)→(7,0,1)→(7,1,0)→(4,1,3)→(4,4,0)

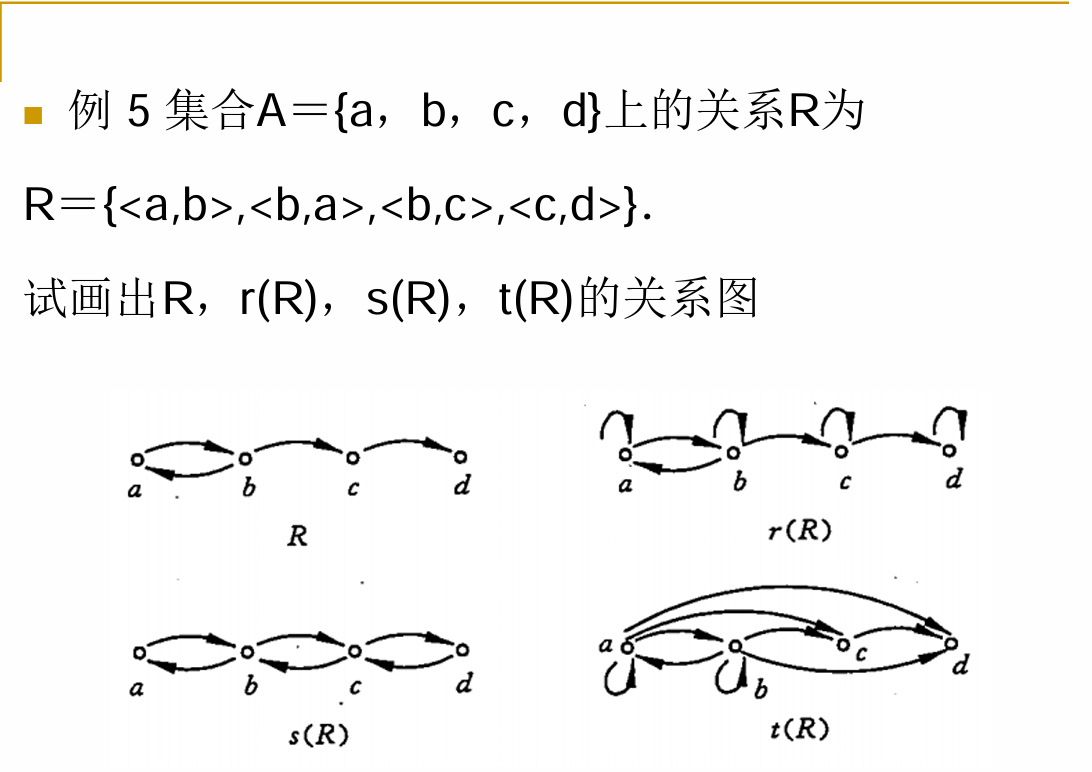
关系图

从图的角度理解关系
定义:设集合X＝{x1，x2，…，xm}，Y＝{y1, y2，… ，yn} ．若R是X到Y的一个关系，则R的关系图是一 个有向图G®＝<V，E>

• 它的顶点集是V＝X∪Y，
• 边集是E：从$x_i到y_j的有向边e_{ij}\in E，当且仅当<x_i,y_i>\in R$

若R是集合X（m个元素）上的一个关系，则R的关系矩阵是m×m方阵.

$R^{-1}$ 的关系矩阵 $M(R^{-1})$ 是R的关系矩阵的转置矩阵

$M(S\circ R)$ 的计算
$M(S\circ R)=M(R)\cdot M(S)$
$(w_{ij})={\bigvee }_{k=1}^m(r_{ik}\wedge s_{kj})$

$M(S\circ R)$ $!=$ $M(R\circ S)$