除法取模与逆元/费马小定理
对于正整数

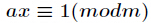
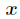


逆元一般用扩展欧几里得算法来求得,如果
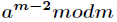
推导过程如下(摘自Acdreamer博客)
![]() 这个为费马小定理,m为素数是费马小定理的前置条件。
这个为费马小定理,m为素数是费马小定理的前置条件。
求a/b=x(mod M)
只要M是一个素数,而且b不是M的倍数,就可以用一个逆元整数b1,通过 a/b=a*b1 (mod M),只能来以乘换除。费马小定理:对于素数 M 任意不是 M 的倍数的 b,都有: b ^ (M-1) = 1 (mod M)
于是可以拆成:b*b^(M-2)=1(mod M)
于是:a/b=a/b*(b * b ^ (M-2))=a*(b ^ (M-2)) (mod M)
求a/b=x(mod M)
用扩展欧几里德算法算出b1,然后计算a*b1(mod M)
exgcd(b,M,x,y); b1=x;
当p是个质数的时候有
inv(a) = (p - p / a) * inv(p % a) % p
证明:
设x = p % a,y = p / a
于是有 x + y * a = p
(x + y * a) % p = 0
移项得 x % p = (-y) * a % p
x * inv(a) % p = (-y) % p
inv(a) = (p - y) * inv(x) % p
于是 inv(a) = (p - p / a) * inv(p % a) % p
然后一直递归到1为止,因为1的逆元就是1
它可以在O(n)的复杂度内算出n个数的逆元








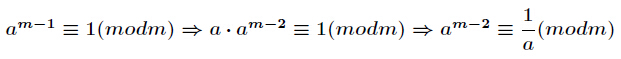














 692
692

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








