【LeetCode】5.Longest Palindromic Substring

关键词：最长回文字串，Manacher算法

问题描述：

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length ofS is 1000, and there exists one unique longest palindromic substring.

即给定一个字符串S，找出它的最长回文字串，回文字串即它等于它反过来构成的字符串。

问题分析：

要找出回文字串，可以枚举回文字串可能的中心，然后从中心向两边展开，注意奇数的回文字串和偶数的回文字串的处理即可，时间复杂度为O(n^2)

class Solution {
public:
    string longestPalindrome(string s) {
        int maxLen = 0;
        int start = 0;
        //odd
        for (int i = 0;i < s.size();++i){
            for (int j = 0;j < s.size();++j){
                int l = i - j;
                int r = i + j;
                if (l < 0 || r >= s.size())break;
                if (s[l] != s[r])break;
                int len = r - l + 1;
                if (len > maxLen){
                    maxLen = len;
                    start = l;
                }
            }
        }
        //even
        for (int i = 0;i < s.size() - 1;++i){
            for (int j = 0;j < s.size();++j){
                int l = i - j;
                int r = i + j + 1;
                if (l < 0 || r >= s.size())break;
                if (s[l] != s[r])break;
                int len = r - l + 1;
                if (len > maxLen){
                    maxLen = len;
                    start = l;
                }   
            }
        }
        return s.substr(start,maxLen);
    }
};

这样就结束了吗？不，我们不满足于O(n^2)的时间复杂度，使用Manacher算法可以在O(n)的时间复杂度内解决这一问题。

Manacher算法的解释可以参考：http://www.cnblogs.com/bitzhuwei/p/Longest-Palindromic-Substring-Part-II.html

这里我想谈一下我对Manacher算法的理解。

文章中提到插入间隔符：

字符串S: aba插入间隔符后变成字符串T: ^#a#b#a#$，以T中的字符b向外扩展，判断回文字，可以得到回文字串#a#b#a#，扩展次数为3，与aba的长度相等。

字符串S: abba插入间隔符后变成字符串T: ^#a#b#b#a#$，以T中的两个字符b之间的字符#向外扩展，判断回文字，可以得到回文字串#a#b#b#a#，扩展次数为4，与abba的长度相等。

因此可以用插入间隔符的方法解决回文字串长度奇偶的问题。

有如下代码：

#include <cstring>
#include <iostream>
#include <string>
#include <vector>
using namespace std;

class Solution {
public:
    string longestPalindrome(string s) {
		int len = s.size();
		string T(len*2+3, '#');
		T[0] = '^';
		T[T.size() - 1] = '$';
		vector<int> p(T.size(), 0);
		for (int i = 0;i < len;++i){
			T[i * 2 + 2] = s[i];
		}
		int C = 0, R = 0;
		for (int i = 2;i < T.size() - 2;++i){
            /*
			int mirror_i = 2 * C - i;
			if (mirror_i >= 0){
				int diff = R - i; 
				if (p[mirror_i] < diff){
					p[i] = p[mirror_i];
					continue;
				}
			}
            */
			while(T[i - p[i] - 1] == T[i + p[i] + 1])++p[i];
			C = i;
			R = i + p[i];
		}
		int id = 0;
		int maxLen = p[id];
		for (int i = 1;i < p.size();++i){
			if (p[i] > maxLen){
				maxLen = p[i];
				id = i;
			}
		}

		return s.substr((id - maxLen - 1) / 2,maxLen);
    }
};

在这段代码中，有一段注释，而这段注释是Manacher算法的精髓。
Manacher算法利用了回文字串的对称性：

使用一个数组p记录每个点作为中心时最长的回文字串长度，

变量C为某个回文字串的中心，变量i表示: 当前需要以点i为中心，计算回文字串的长度。

i'为i关于C的对称点

， 红色为以C为中点的回文字串。

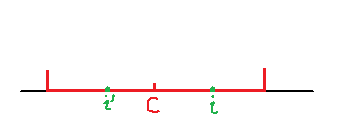
分为两种情况处理：

1.

 

已计算i'为中心的最长回文字串，该回文字串在以C为中心的回文字串里面，求p[i]

由以C为中心的回文字串的对称性可知, p[i] = p[i']

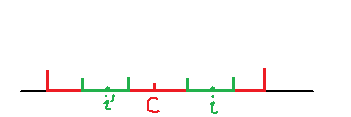
2.

以i'为中心的回文字串有一部分不在以C为中心的回文字串中，这时无法利用对称性了:-( 因此，以i为中心向两边扩展求p[i]

算法的伪代码：

C = 0

for i = 0 -> 总字符串的长度-1{

  i' = 2 * C - i;

   if i' >= 0 and 可以利用对称性(i, C){

      p[i] = p[i'];

   }else{

      以i为中心向两边扩展，求p[i];

      C = i;

   }

}

这里涉及到一个问题，C如何取值？

在情况1中，i关于C的对称点i', 以i'为中心的回文字串一直在以C的回文字串中，因此C可以固定

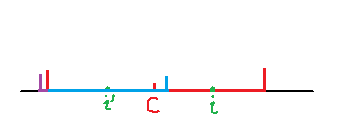
在情况2中，记以C为中心的回文字串为W，从i到W的右边界可能还存在回文字串能够利用W的对称性，从C到i中的点选一个作为中心，其构成的回文字串的对称性也有可能被后续的i利用。

我觉得在不能利用当前的C的对称性时令C = i, 没有充分地利用所有对称性质，是为了算法设计的方便吧~