标定系列解读 | 相机激光标定算法：从理论到实践

旷视MegMaster机器人系列是旷视自主研发的一系列AI智能机器人硬件设备，基于旷视全球领先的人工智能算法及机器人技术，可实现搬运、分拣、托举、存储等功能，被广泛应用于物流仓储、工厂制造等场景。旷视研究院SLAM组主要负责多传感器建图、定位、标定等工作，在开发过程中总结了一些理论和实践方面的经验教训，在此分享出来，希望能够与大家一起探讨，为机器人行业贡献自己的绵薄之力。

近期，旷视研究院推出了机器人多传感器标定的系列内容，包括:

• 标定系列一 | 基础理论分析：https://zhuanlan.zhihu.com/p/93183788

• 标定系列二 | 实践之Camera-Odometry标定：https://zhuanlan.zhihu.com/p/101727151

• 标定系列三 | 实践之Camera-Lidar标定

本文是标定系列解读第三篇，介绍了Camera-Lidar标定，通过对一些基础知识和小细节进行讨论和理论推导，给出了一些可以提升标定精度的改进建议。另外本文还给出了一个简单的开源代码对上述标定原理进行实践，以及提供了一个仿真程序，可以直观感受标定数据对系统可观性的影响。希望能够给大家一些启发。

目录

1. 前言

2. 理论

    2.1 基于平面约束的相机激光标定算法

        2.1.1 平面约束

        2.1.2 2D 激光和相机外参数初始值求解

        2.1.3 3D 激光和相机外参数初始值求解

        2.1.4 外参数优化

    2.2 推论：所有平行的平面提供的约束等价。

    2.3 拓展：标定板的边界约束

3. 实践

    3.1 代码梳理和上手操作

    3.2 仿真代码的特别说明

        3.2.1 系统可观性的判断

        3.2.2 利用仿真代码验证平行平面提供的约束等价

        3.2.2 利用仿真代码指导采集数据：如何充分旋转标定板

4. 结语

5. 参考文献

 

1. 前言

从理论上看，相机和激光之间外参数的标定原理非常简单，但在实际标定过程中，特别是一个初学者采集数据进行标定时，却发现标定结果非常不理想。如何采集有效的标定数据（何种运动轨迹，如何晃动标定板）对于激光相机标定而言非常重要。

读完本文，你会发现原来采集数据时标定板和传感器之间只做纯粹的平移运动是没有意义的。本文也对相机激光标定的一些基础知识和小细节进行讨论，主要贡献点有三：

1. 从理论开始对激光（单线、多线都适用）和相机外参数的标定进行简要推导（公式多但简单），然后给出一些可以提升标定精度的改进建议。

2. 给出一个简单的开源代码对上述标定原理进行实践。

3. 提供一个仿真程序，可以直观感受标定数据对系统可观性的影响。

2. 理论

通常，标定激光和相机之间的外参数有两类方法：一类是利用 3D-3D 的约束，即利用激光测量的三维激光点 (3D) 和相机测量的标定板三维坐标 (3D) 两者来构建约束；另一类是利用 3D-2D 的约束，即利用激光测量的三维激光点 (3D) 和图像二维特征（2D、点特征、线段特征）来构建约束。

本文主要讲解利用 3D-3D 约束来进行外参数标定的方法，而 3D-2D 这一方法和 PnP 或 PnL 问题类似，这里不做展开。另外，标定过程的通常做法是先利用少量观测求解外参数的初始值，然后利用多帧数据的约束进行最小二乘优化对初始值进行 refine。接下来，将按照这个逻辑对标定算法进行讲解并推荐一些改进的算法。

2.1 基于平面约束的相机激光标定算法

如下图所示，相机可以通过标定板平面的二维码或棋盘格来计算标定板平面在相机坐标系下的表示。同时，激光发出的光束落在标定板平面上（图中红点），利用激光点在激光坐标系下的坐标和平面方程在相机坐标系下的坐标，构建点在平面上的约束从而求解外参数。

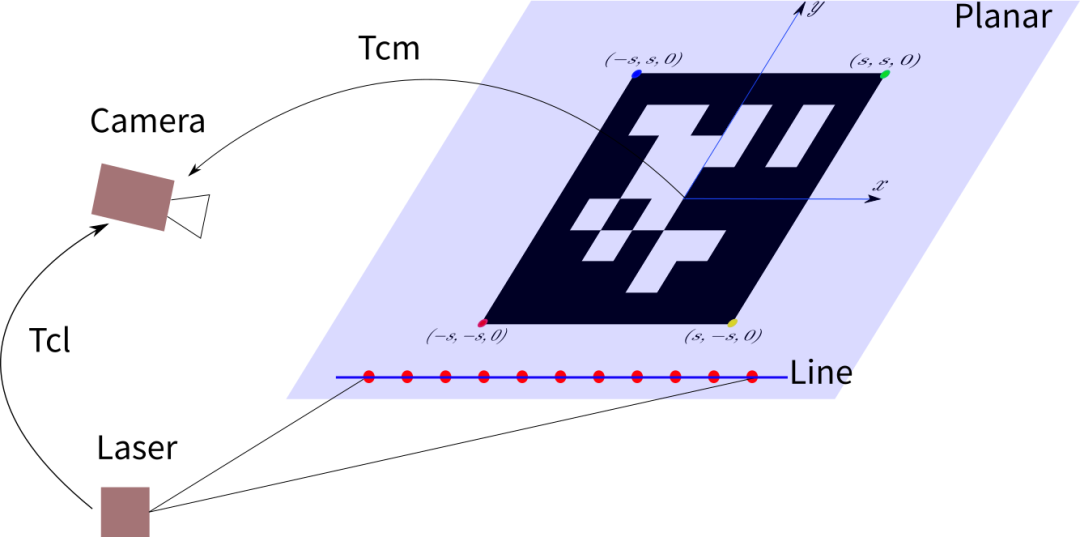
 2.1.1 平面约束

假设标定板平面在相机坐标系中的参数为，其中是平面的三维法向量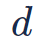，是相机坐标系原点到平面的距离。平面上的一个三维点在相机坐标系下的坐标为，点在平面上满足：

 

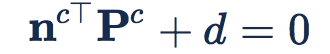
假设从激光坐标系到相机坐标系之间的旋转和平移为。如果知道激光坐标系中某个激光点落在标定板上，则通过点在平面上这个约束能够构建关于外参数的方程：

上述方程能够提供一个约束，通过多个这样的约束就能求解外参数。求解时，一个直观的想法是利用 g2o 或者 ceres 等优化工具构建非线性最小二乘进行优化求解。但是对于非线性最小二乘问题，需要知道外参数的一个初始值，如果初始值不准确，则有可能会优化到局部最小值。因此，一个合理的求解流程应该是闭式解提供初始值，对该初始值利用多帧数据进行优化，得到更准确的标定结果。

虽然平面约束对于 2D 激光和 3D 激光而言是一样的，但 2D 激光和 3D 激光闭式求解外参数的方式稍有不同。因为 3D 激光的激光点更多，从而可以直接计算激光点云的法向量，利用这个法向量简化外参数计算流程，下文将详述。接下来，介绍 2D 激光和相机外参数的求解。

2.1.2 2D 激光和相机外参数初始值求解

这里主要参考 2004 年 Zhou 等人的论文【1】，该论文是比较早期的工作，求解思路清晰。论文中估