目录
1. 猜数字大小II
https://leetcode.cn/problems/guess-number-higher-or-lower-ii/description/
我们正在玩一个猜数游戏,游戏规则如下:
- 我从
1到n之间选择一个数字。 - 你来猜我选了哪个数字。
- 如果你猜到正确的数字,就会 赢得游戏 。
- 如果你猜错了,那么我会告诉你,我选的数字比你的 更大或者更小 ,并且你需要继续猜数。
- 每当你猜了数字
x并且猜错了的时候,你需要支付金额为x的现金。如果你花光了钱,就会 输掉游戏 。
给你一个特定的数字 n ,返回能够 确保你获胜 的最小现金数,不管我选择那个数字 。
示例 1:

输入:n = 10 输出:16 解释:制胜策略如下: - 数字范围是 [1,10] 。你先猜测数字为 7 。 - 如果这是我选中的数字,你的总费用为 $0 。否则,你需要支付 $7 。 - 如果我的数字更大,则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。 - 如果这是我选中的数字,你的总费用为 $7 。否则,你需要支付 $9 。 - 如果我的数字更大,那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏,总费用为 $7 + $9 = $16 。 - 如果我的数字更小,那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏,总费用为 $7 + $9 = $16 。 - 如果我的数字更小,则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。 - 如果这是我选中的数字,你的总费用为 $7 。否则,你需要支付 $3 。 - 如果我的数字更大,则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。 - 如果这是我选中的数字,你的总费用为 $7 + $3 = $10 。否则,你需要支付 $5 。 - 如果我的数字更大,那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏,总费用为 $7 + $3 + $5 = $15 。 - 如果我的数字更小,那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏,总费用为 $7 + $3 + $5 = $15 。 - 如果我的数字更小,则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。 - 如果这是我选中的数字,你的总费用为 $7 + $3 = $10 。否则,你需要支付 $1 。 - 如果我的数字更大,那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏,总费用为 $7 + $3 + $1 = $11 。 在最糟糕的情况下,你需要支付 $16 。因此,你只需要 $16 就可以确保自己赢得游戏。
示例 2:
输入:n = 1 输出:0 解释:只有一个可能的数字,所以你可以直接猜 1 并赢得游戏,无需支付任何费用。
示例 3:
输入:n = 2 输出:1 解释:有两个可能的数字 1 和 2 。 - 你可以先猜 1 。 - 如果这是我选中的数字,你的总费用为 $0 。否则,你需要支付 $1 。 - 如果我的数字更大,那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏,总费用为 $1 。 最糟糕的情况下,你需要支付 $1 。
提示:
1 <= n <= 200
1.1 题目解析
题目本质
这是一个博弈论中的 Minimax 问题。你需要设计一个猜测策略,使得在对手恶意选择(总是让你花最多钱)的情况下,你的最大损失最小化。本质上是求"在区间 [1,n] 中,第一次猜哪个数,能让最坏情况的代价最小"。
常规解法
最直观的想法是贪心:每次都猜中间的数,类似二分查找。因为这样看起来能让左右区间尽可能平衡,减少最坏情况的深度。
问题分析
但贪心策略忽略了一个关键点:代价不仅和猜测次数有关,更和猜测的数字大小有关。猜 10 比猜 1 代价高 10 倍!而且每个子区间的最优策略是递归的,不能简单地用二分。这是一个需要考虑所有可能性的决策问题,暴力枚举的复杂度是指数级。
思路转折
要想高效求解,必须认识到这是一个区间 DP 问题。对于任意区间 [start, end],我们需要:
① 尝试第一次猜每个数 i;
② 递归求解左右子区间的最优代价;
③ 选择让"最坏情况代价最小"的 i;
由于区间问题有大量重叠子问题(比如 [1,5] 可能被 [1,10] 和 [1,8] 重复计算),使用记忆化搜索可以将复杂度降到多项式级别。
1.2 解法
算法思想
使用记忆化递归(自顶向下 DP)。定义 dfs(start, end) 表示在区间 [start, end] 中保证猜对的最小准备金。状态转移方程为:
dfs(start, end) = min { i + max(dfs(start, i-1), dfs(i+1, end)) }
i∈[start,end]
↑ ↑
外层取min 内层取max
(你选最优策略) (对手恶意选择)i)初始化: 创建二维数组 memo[n+1][n+1],全部填充为 -1 表示未计算。
ii)递归边界: 当 start >= end 时返回 0,因为只有一个数或区间为空时不需要猜测。
iii)遍历猜测: 对于区间 [start, end],遍历每个可能的第一次猜测 i:
-
计算左子区间 [start, i-1] 的最优代价 left
-
计算右子区间 [i+1, end] 的最优代价 right
-
当前猜测的代价 cost = i + max(left, right)
iv)选择最优: 在所有 i 的代价中,选择最小的作为该区间的答案。
v)记忆化: 将结果存入 memo[start][end],避免重复计算。
易错点
-
代价计算错误: cost = max(left, right) + i,不是 +1。因为猜数字 i 的代价就是 i 本身,不是固定值。
-
边界条件混淆: 当 start == end 时应返回 0(只有一个数,直接猜对不花钱),而不是返回 start。
-
max/min 顺序搞反: 内层用 max 是因为对手恶意选择(取最坏情况),外层用 min 是因为你选最优策略。
1.3 代码实现
class Solution {
int[][] memo;
int n;
public int getMoneyAmount(int _n) {
n = _n;
memo = new int[n + 1][n + 1];
for(int[] x : memo) {
Arrays.fill(x, -1);
}
return dfs(1, n);
}
public int dfs(int start, int end) {
// 区间长度<=1,不需要猜测
if(start >= end) return 0;
// 已计算过,直接返回
if(memo[start][end] != -1) return memo[start][end];
int ret = Integer.MAX_VALUE;
// 尝试第一次猜每个数i
for(int i = start; i <= end; i++) {
// 如果猜i,答案在左边[start, i-1]的代价
int left = dfs(start, i - 1);
// 如果猜i,答案在右边[i+1, end]的代价
int right = dfs(i + 1, end);
// 猜i的代价 = i + 最坏情况(对手恶意选择左或右)
int cost = i + Math.max(left, right);
// 在所有第一次猜测中,选择最优的
ret = Math.min(ret, cost);
}
memo[start][end] = ret;
return ret;
}
}复杂度分析
-
时间复杂度:O(n³)。共有 O(n²) 个状态(所有可能的区间),每个状态需要遍历 O(n) 个猜测位置
-
空间复杂度:O(n²)。记忆化数组和递归栈的空间开销。
2. 矩阵中的最长递增路径
https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/description/
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
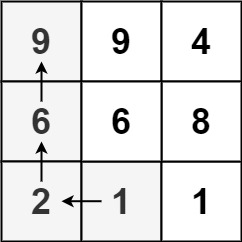
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
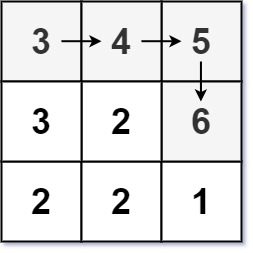
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]] 输出:1
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 231 - 1
2.1 题目解析
题目本质
这是在有向无环图(DAG)上求最长路径的问题。矩阵中的每个格子是节点,只能从小的数走向大的数(单向边),天然保证无环。本质上是"从每个起点出发,沿着递增方向能走多远"。
常规解法
最直观的想法是对每个格子都做一次 DFS,搜索从该格子出发的所有递增路径,取最长的那条。总共 m×n 个起点,每个都暴力搜一遍。
问题分析
暴力 DFS 会有大量重复计算。比如路径 1→2→6→9 和 3→6→9,计算 1 的最长路径时会算一遍"6 的最长路径",计算 3 的最长路径时又要重新算一遍。
一个格子可能被访问指数级次数,复杂度接近 O(2^(m×n)),对于 200×200 的矩阵必然超时。
思路转折
要想高效必须避免重复计算,关键观察是:某个格子的"最长递增路径长度"是固定的,无论从哪个起点到达它都一样。因此可以用记忆化搜索:
第一次计算某个格子时缓存结果,后续直接读取。由于是 DAG(递增路径不会成环),不需要回溯标记,记忆化就能完美工作。复杂度降到 O(m×n),每个格子只计算一次。
2.2 解法
算法思想
使用记忆化 DFS(自顶向下 DP)。定义 dfs(i, j) 表示从格子 (i, j) 出发的最长递增路径长度。状态转移为:
dfs(i, j) = 1 + max { dfs(x, y) }
对所有满足 matrix[x][y] > matrix[i][j] 的相邻格子 (x, y)如果四周没有更大的数,则 dfs(i, j) = 1(只有自己)。
i)初始化: 创建 memo[m][n] 数组,用 -1 标记未计算(或用 0,因为路径长度至少为 1)。
ii)遍历起点: 对矩阵每个格子 (i, j) 调用 dfs(i, j),维护全局最大值。
iii)DFS 递归:
-
如果 memo[i][j] 已计算过,直接返回
-
否则初始化 ret = 1(当前格子本身)
-
遍历上下左右四个方向,如果相邻格子值更大,递归计算其最长路径
-
取所有有效方向的最大值 +1
iv)记忆化: 将计算结果存入 memo[i][j],避免重复计算。
v)返回答案: 所有起点中的最大值即为答案。
易错点
-
memo 初始化: 而且要先 memo = new int[m][n] 初始化,否则访问 null 会报错。
-
误用 vis 数组: 容易惯性地加 vis[x][y] = true/false 来防止重复访问。但递增路径天然无环(不可能从 5 走到 6 再回到 5),不需要回溯标记,加了反而会出错。
-
返回值处理错误:正确写法是 ret = Math.max(ret, dfs(matrix, x, y) + 1)。
-
累加逻辑混淆: 不是把四个方向都加起来,而是取其中最长的一条路径。用 Math.max 而不是连续 ret++。
2.3 代码实现
class Solution {
int[] dx = {1, -1, 0, 0};
int[] dy = {0, 0, -1, 1};
int m, n;
int[][] memo;
public int longestIncreasingPath(int[][] matrix) {
m = matrix.length;
n = matrix[0].length;
memo = new int[m][n];
// 默认值0表示未计算(路径长度至少为1,不会是0)
int ret = 1;
// 尝试每个格子作为起点
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
ret = Math.max(ret, dfs(matrix, i, j));
}
}
return ret;
}
public int dfs(int[][] matrix, int si, int sj){
// 已计算过,直接返回
if(memo[si][sj] != 0) return memo[si][sj];
int ret = 1; // 当前格子本身长度为1
// 尝试四个方向
for(int i = 0; i < 4; i++){
int x = si + dx[i], y = sj + dy[i];
// 边界检查 + 递增条件
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[si][sj]){
// 取四个方向中最长的路径 + 1
ret = Math.max(ret, dfs(matrix, x, y) + 1);
}
}
memo[si][sj] = ret;
return ret;
}
}复杂度分析
-
时间复杂度:O(m×n)。每个格子只计算一次(记忆化),每次计算需要检查 4 个方向,总体为 O(4×m×n) = O(m×n)。
-
空间复杂度:O(m×n)。memo 数组占用 O(m×n) 空间,递归栈最深为矩阵中最长路径的长度,最坏 O(m×n)。























 223
223

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








