Bellman-Ford算法之单源最短路径问题

Bellman-Ford算法之最短路径问题

问题：求下图中点S到T的最短路径。

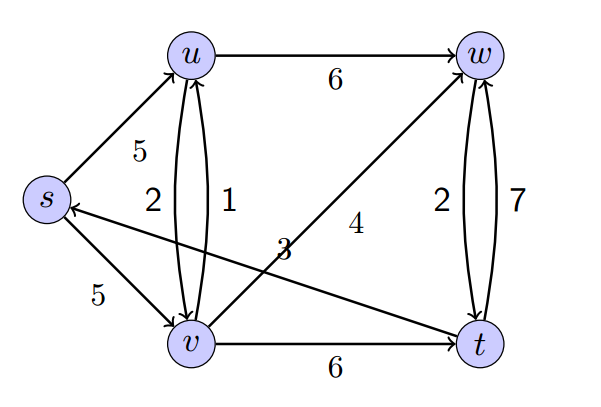
分析：这个问题于TSP问题有点像，不同点在于该问题不需要每个节点都遍历。对于大问题节点太多，眼花缭乱，不会做。先尝试把其分解成子问题，变得容易点。
step 1:从s到t的路径，这个过程我们可以看做是一系列的决策，在每个决策步考虑下一步怎么走。
step 2:假装已经拿到了最优解O，考察O中的第一个决策：所有s的邻居节点都是备选选，这样选择了从s到v的一条路径。
step 3:剩下的问题是从v中如何走到 t，路径越短越好。
但是按照上面的递归表达式写程序还是有点慢，因为子问题太多，图上的递归都是指数级。我们引入新观察，因为图中没有福泉，所以从s到t的最短路径做多经过n个节点即k条边(k=n-1)。从而进一步修整了我们的子问题，写出递归表达式如下：

$OPT[v,t,k] =min \begin{cases} OPT[v,t,k-1] &\\[2ex] min {{ {(w,v\in E) OPT[w,t,k-1]+d(v,w) }} }\ \end{cases}$

例子：对下图交通网络图，求个点到达点t的最短路径。

为方便求解，设置节点a,b,c,d,e,t分别为1，2，3，4，5，6。
程序实现过程如下：

#include<stdio.h>
#define non  65535 
int n=6;//节点个数 
int m=10;//遍的个数 
struct edge{
    int u;//边起点 
    int v;//边的端点 
    int w;//边的权值 
}Edge[10]={ {1,2,-4},{1,6,-3}, {2,4,-1},{2,5,-2},
            {3,2,8},{3,6,3}, {4,6,4},{4,1,6},{5,3,-3},
            {5,6,2}};
int min(int a,int b){
    return a>b?b:a;
}
int d(int a,int b){
    int i;
    for(i=0;i<m;i++){
        if(Edge[i].u==a&&Edge[i].v==b)
            return Edge[i].w;
    }
    return non;
} 
void Bellman_Ford(int OPT[][6]){
    int v,j,k,w,i;
    int min_temp=non;
    //初始化数组 
    for(v=1;v<n;v++)
        OPT[v][0]=non;
    for(k=0;k<n;k++)
        OPT[0][k]=0;    
    for(k=1;k<n ;k++){
        for(v=1;v<n;v++){
            if(k==1 ){
                OPT[v][k]=d(v,6);//一步到达 from v to t
            }
            else{
                for(w=0;w<6;w++){
                    if(OPT[w][k-1]!=non  &&  d(v,w)!=0 ){
                        min_temp=OPT[w][k-1]+d(v,w);
                        break;      
                    }
                }
                for(w=0;w<6;w++){
                    if(OPT[w][k-1]!=non && d(v,w)!=0 ){
                       if(min_temp>(OPT[w][k-1]+d(v,w)) ) 
                        min_temp=OPT[w][k-1]+d(v,w);
                    }   
                }
               OPT[v][k]=min( (OPT[v][k-1])  ,min_temp );       
              }
        }       
    }
    printf("第0步    第1步   第2步   第3步   第4步   第5步\n");
    for(v=0;v<6;v++){
        for(k=0;k<6;k++){
            printf("%7d",OPT[v][k]);
        }
        printf("\n");
    }
    for(i=1;i<=5;i++)
        printf("从第 %d 个节点到6号节点的Shortest Path=%d \n",i,OPT[i][5]);
}
void main(){
    int OPT[6][6];  
    Bellman_Ford(OPT);
}

运行结果如下：

总结:前几天老师课堂上讲了该算法，由于今天天没什么事，就想着自己来实现下这个Bellman-Ford算法。感觉在图上做递归比在数组上做递归还是酷些。