红黑树

二叉搜索树是一个优雅的字典数据类型的实现,它支持查找、插入、删除和可能的额外操作。对于简单操作来说，其主要缺点是最坏情况下的时间复杂度Ω（n）。其原因是，插入和删除往往会导致树的不平衡。而二叉搜索树可以抵消这种偶尔本地重组操作并保证每个操作数时间。

2-3-4树 一种特殊类型的平衡树是2-3-4树。每个内部节点存储一个、两个或三个项，相对应有两个、三个或四个孩子。每个叶子具有相同的深度。如图15所示，在内部节点的项分别存储在子树中，从而促进快速搜索。

图15：高度为2的2-3-4树。所有的数据项存储在内部节点上

在图15中最小的2-3-4树中高度为h，每个内部节点有两个孩子，所以我们有2h个叶节点2h-1个内部节点。在高度为h的最大2-3-4树，每一个内部节点有四个孩子，所以我们有4h个叶节点和(4h-1)/3个内部节点。我们可以在二叉搜索树中存储一个2-3-4树通过展开一个节点的第i>1项和在这个节点上的第i+1个子节点上的每个项,如图16所示。

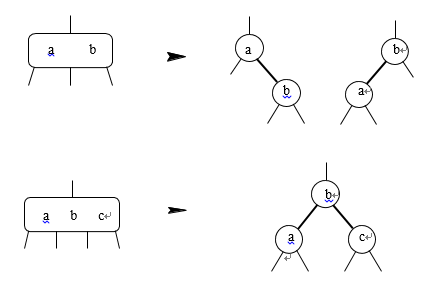
图16：将2-3-4树转换为二叉树。加粗边称为红色和其它边被称为黑色

红-黑树 假设我们二叉搜索树的每个边不是红色就是黑色。颜色被方便地存储在边的下级节点。像这样的边颜色树就是是红黑树：
（1）任何向下查找的路径上没有两个连续的红色边、每个最大的路径以一个黑色的边节点结束；
（2）所有极大向下路径有相同数量的黑色边。

最大向下路径上面的黑色边节点数量称为黑色高度，表示为bh(ρ). 当我们把一个2-3-4树转换为像图16中二叉树时，我们得到了一个红黑树。图15转化的树的结果如图17所示。

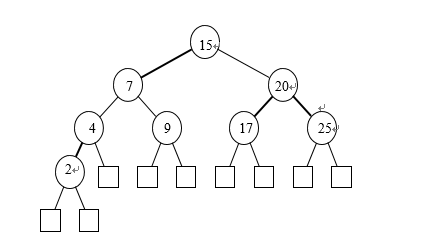
图17：从图15中2-3-4树得到的红黑树

高度定理：红黑树n个节点具有的高度至多是2 log2 (n + 1)

证明：叶子的数量是n+ 1。设每个红边得到2-3-4树具有n+ 1个叶子节点。它的高度为h ≤ log2(n + 1)。我们有bh(ρ) = h，并通过规则(1)红黑树的高度是至多2bh(ρ)≤2 log2 (n + 1)。

旋转：一个转动要移动一个子树从一侧到另一策，重组一个红黑树只能与一个操作（和其对称的版本）进行，如图18。在图18中的左树节点的有序序列为
… , order(A), ν , order(B) , µ , order(C ) , …
这也是在右树节点的有序序列。 换句话说，每次转动都会保持这样的排序。以下功能ZIG实现了向右旋转。

图18：从左至右右旋转和从右到左左旋转

Node ∗ ZIG(Node ∗ µ)
assert µ = NUL L and ν = µ → ℓ = NULL;
µ → ℓ = ν → r; ν → r = µ; return ν.
功能ZAG是对称的，并且执行左旋转。偶尔，需要依次执行两次旋转，为了方便我们将它们组合成一个简单的操作称为双旋转，如图19所示。我们用一个函数ZIG ZAG实现双右旋转和对称函数ZAGZIG实现双左旋转。

图19：在μ上进行双右旋转是一个在v上简单的左旋转和μ一个右旋转

Node ∗ ZIGZAG(Node ∗ µ)
µ → ℓ = ZAG(µ → ℓ); return ZIG(µ).
双右旋转由两个简单的旋转组成：ZIGZAG(µ) = ZIG(µ) ◦ ZAG(ν).。请记住，函数的构成是从右向左书写，所以v单左旋转在μ的单右旋转之前。单旋转节点的顺序等于双旋转的顺序。

插入：在红黑树算法改进细节研究之前，我们看一下树中出现的短的插入序列，如图20所示。再插入10，7，13，4，我们有两个红边在这个序列里和修复它生成10（A），再次加入2，我们修复序列里的两条红边通过一个简单的7（B）旋转，然后加入5，生成4（C），再加入6，我们得到双旋转7（D）。

图20：通过插入项10, 7, 13, 4, 2, 5, 6得到的红黑树序列

一个项目X通过替换一个新的内部节点作为一个子节点添加到合适的位置上。为了满足规则（2）的红黑树定义，将新插入的节点变成红色，如图21所示。开始颜色的调整和这个新节点的父节点v的结构调整。

图21：新插入的节点，将边的颜色变成红色

根据这个算法，找到一个适用于节点ν的不变量，通过插入算法可以保持这个属性。

不变量I：唯一可能违反红黑树规则就是节点V的规则（1），如果v有流入的红色边，然后它正是一个红色的流出边。
观察得出在插入x之后，变量1保持在右边。我们继续分析可能出现的所有情况：本地调整操作取决于临近节点v。
情况1 进来的v边是黑色的。完成
情况2 进来的v边是红色的。让µ成为v的父节点并假定v是µ的左孩子。
情况2.1 µ的出边都是红色，如图22所示，提升µ，让v成为µ的父节点并递归。

图22：µ的提升（v出边的颜色可能是另一条环路）

情况2.2 只有µ的出边是红色，也就是从µ到v的那条边
    情况2.2.1  v的左输出边是红色，如图23左边所示，右旋转µ，完成。

图23：左边图是µ的右旋转，右边图是双右旋转

    情况2.2.2  v的右输出边是红色，如图23的右边。双右旋转µ。完成

情况2有一个对称的性质是左右可以相互交换。一个插入可能引起对数般的上升，但最多是两次转换。

删除： 先找到要被移除的节点π。如果有必要，我们可以为了π替代中序的继承节点，所以我们可以假设π的所有子节点都是叶子节点。如果π是最后一个中序节点，我们替代对称的那一个。通过一个叶子节点v代替π，如图24所示。如果π的入边是红色的改变其颜色为黑色。另外，记住v的入边为“双黑色”，记为两条黑边。与插入相似，它有助于在保持一个属性的形式上理解这个删除算法。

不变量D 红黑树唯一可能的违规就是v的双黑色入边。

图24：节点π的删除。当我们计算黑边高度时将虚边视为两个黑边

在删除π后不变量D保持在右边。我们现在分析所有可能出现的情况。调整操作的选择取决于v的邻近点。

情况1：v的输入边是黑色。完成。
情况2：v的输入边是双黑色，让µ成为父节点，使κ成为v的兄弟节点，假设v是µ的左边子节点，记κ是内部节点，
情况2.1：从µ到κ的边是黑色的
情况2.1.1 κ的出边都是黑色的，如图25，降级µ，递归从ν = µ

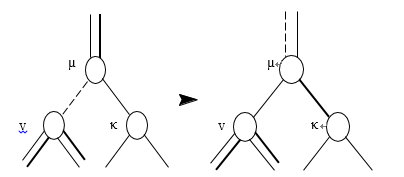
图25 µ的降级

    情况2.1.2  κ的右出边是红色，如图26的左边。改变这个边的颜色为黑色然后左转动μ，完成。

图26 左边图是μ的左转动，右边是双左转动
情况2.1.3 κ的右出边是黑色，如图26的右边。改变这个边的颜色为黑色然后双左转动μ，完成。
情况2.2从µ到κ的边是红色的，如图27所示。左转µ，递归至v

图27 µ的左转
情况2有一个对称的性质是在ν是μ的右孩子时。情况2.2似乎是有问题的因为这个递归没有任何移动v使其更接近于根节点。然而，结构排除了情况2,2再一次发生的可能性。如果我们进入情况2.1.2或者2.1.3那么将会立即终止。如果我们进入2.1.1然后也会跟随者终止，因为进入µ的边是红色的。删除会导致算法上对数般的降级，但最多也就是三个转动。

总结：红黑树是一个字典数据类型的实现，支持查找、插入、删除操作且每个操作的时间复杂度均为对数复杂度。一个插入或者删除的请求相当于三个单次转动的操作。红黑树同时也支持查找最大、最小项以及给定一个节点的后继节点父节点，均为对数时间复杂度。