树和二叉树
1:定义:(虽然没什么鸟用,但是需要了解)树(Tree)是N个节点的有限集
非空树 T:
(1) 有且只有一个根节点(文件的目录接口,\根目录)
(2) 除了根节点外以外多个互相不想交的有限集。。。。
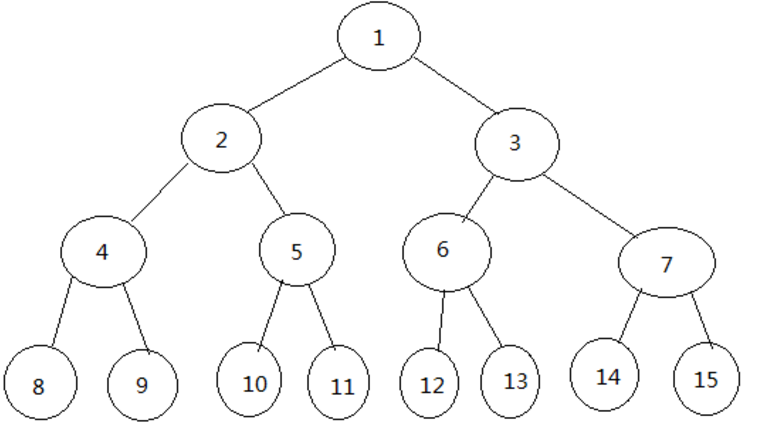
2: 不说了来一棵树(二叉树)二叉树是重点学习的。
3:名词解释(需要知道)
节点:树的独立单元,就是每个圆圈
节点的度:节点拥有的字数(图中为二叉树)节点都为2,除了叶子节点外;
树的度:就是树内节点度的最大值。二叉树的最大节点就是2
叶子:没有孩子的树,例如 8 9 10 11..
双亲和孩子:例如 5的双亲为2,5的孩子为10 11
兄弟:同一个父亲 10 11 就是兄弟节点 10与12是堂兄弟,堂兄弟就是在同一层
层次:就是几行, 1 是第一层,2 3 是第二层么以此类推
深度:树节点的最大层数,(貌似就是层数)上图;层数为4,深度为4
4:
二叉树:一个根节点,分支有左右之分不能颠倒
二叉树的基本形态:重要,便于理解递归
1)空树;
2)只有根的树,即单结点;
3)有根且有一个左子树;
4)有根且有一个右子树;
5)有根且有一个左子树,有一个右子树。
5:二叉树的性质:
1:在二叉树I层上最多有2^(i-1) 第一层 =0 ,第二层最多2个 =2
2:深度为K的二叉树最多有-1个节点。第一层1个 第二层 3个如图
3:(灰常重要)对于任意的二叉树T:如果其终端节点的个数为(叶子节点),度为2的节点为 =+1;(考试或者笔试题目)
满二叉树:每一层都是满的,每一层的节点数都有其最大节点数
完全二叉树:叶子节点只能在最后两层出现








 本文介绍了二叉树的基本概念,包括树的定义、二叉树的性质,如节点的度、树的度、叶子节点、双亲和孩子、兄弟等。特别强调了二叉树的五种基本形态,并探讨了满二叉树和完全二叉树的特点。内容涵盖了二叉树的深度、层次等关键知识点,适合算法和数据结构学习者参考。
本文介绍了二叉树的基本概念,包括树的定义、二叉树的性质,如节点的度、树的度、叶子节点、双亲和孩子、兄弟等。特别强调了二叉树的五种基本形态,并探讨了满二叉树和完全二叉树的特点。内容涵盖了二叉树的深度、层次等关键知识点,适合算法和数据结构学习者参考。














 1392
1392

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








