最近写作业时遇到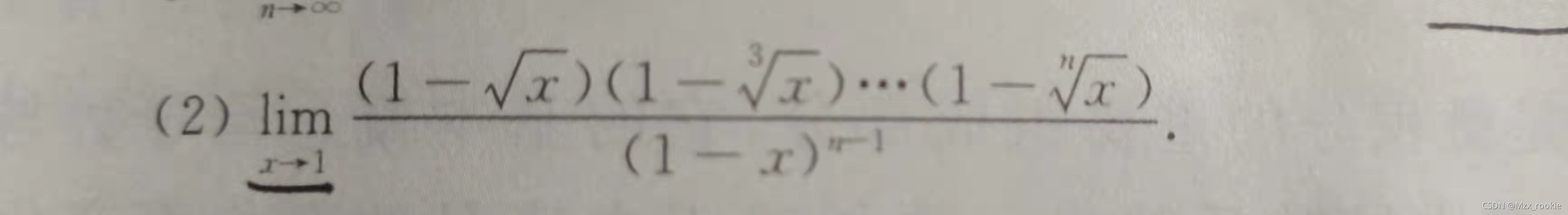
作为数学萌新的我属实没能很快解决,于是我便试着照搬n次方差公式试一下
然而我只是单纯的把n替换成了对应的1/n,结果就是还是没能得出想要的结果。
最后看了答案,再进行反推时,得出一个粗略的n分之一次方差公式
本来以为这是特殊的n次方差公式,可在网上怎么也找不到
但我定睛一看,发现原式可以这么变,就可以通用了↓
这个我在网上也是找了很久没找到(可能是我的检索关键词不对吧),反正我就先发在这了。
最近写作业时遇到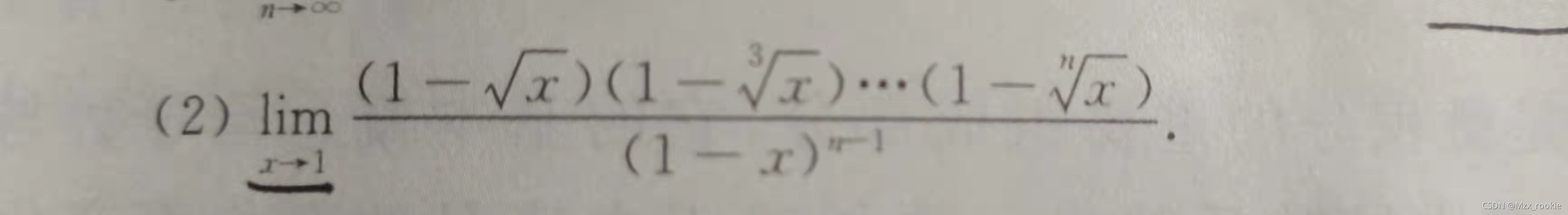
作为数学萌新的我属实没能很快解决,于是我便试着照搬n次方差公式试一下
然而我只是单纯的把n替换成了对应的1/n,结果就是还是没能得出想要的结果。
最后看了答案,再进行反推时,得出一个粗略的n分之一次方差公式
本来以为这是特殊的n次方差公式,可在网上怎么也找不到
但我定睛一看,发现原式可以这么变,就可以通用了↓
这个我在网上也是找了很久没找到(可能是我的检索关键词不对吧),反正我就先发在这了。

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


